Merkle Tree(默克尔树)算法的 查询(不是查询节点用的,而是查询错乱节点),新建,更新
fei33423 Merkle Tree
注意比特币的 tree , spv 简单支付证明,先通过服务端找到交易的块. 即证明了.
Merkle Tree概念
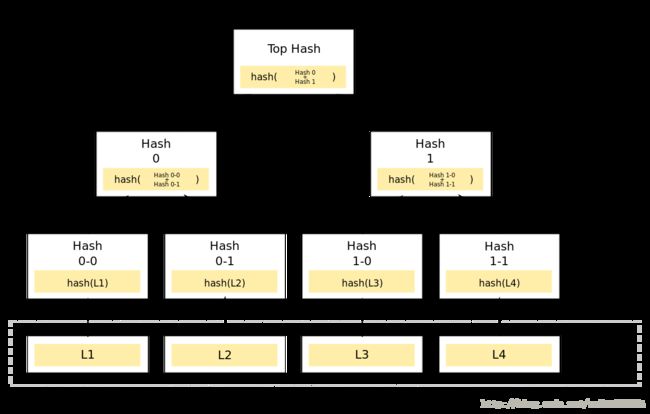
Merkle Tree,通常也被称作Hash Tree,顾名思义,就是存储hash值的一棵树。Merkle树的叶子是数据块(例如,文件或者文件的集合)的hash值。非叶节点是其对应子节点串联字符串的hash。[1]
phil 注: 这张图,有误导作用.节点不一定是2^n 次方.
1、Hash
Hash是一个把任意长度的数据映射成固定长度数据的函数[2]。例如,对于数据完整性校验,最简单的方法是对整个数据做Hash运算得到固定长度的Hash值,然后把得到的Hash值公布在网上,这样用户下载到数据之后,对数据再次进行Hash运算,比较运算结果和网上公布的Hash值进行比较,如果两个Hash值相等,说明下载的数据没有损坏。可以这样做是因为输入数据的稍微改变就会引起Hash运算结果的面目全非,而且根据Hash值反推原始输入数据的特征是困难的。[3]

如果从一个稳定的服务器进行下载,采用单一Hash是可取的。但如果数据源不稳定,一旦数据损坏,就需要重新下载,这种下载的效率是很低的。
2、Hash List
在点对点网络中作数据传输的时候,会同时从多个机器上下载数据,而且很多机器可以认为是不稳定或者不可信的。为了校验数据的完整性,更好的办法是把大的文件分割成小的数据块(例如,把分割成2K为单位的数据块)。这样的好处是,如果小块数据在传输过程中损坏了,那么只要重新下载这一快数据就行了,不用重新下载整个文件。
怎么确定小的数据块没有损坏哪?只需要为每个数据块做Hash。BT下载的时候,在下载到真正数据之前,我们会先下载一个Hash列表。那么问题又来了,怎么确定这个Hash列表本事是正确的哪?答案是把每个小块数据的Hash值拼到一起,然后对这个长字符串在作一次Hash运算,这样就得到Hash列表的根Hash(Top Hash or Root Hash)。下载数据的时候,首先从可信的数据源得到正确的根Hash,就可以用它来校验Hash列表了,然后通过校验后的Hash列表校验数据块。 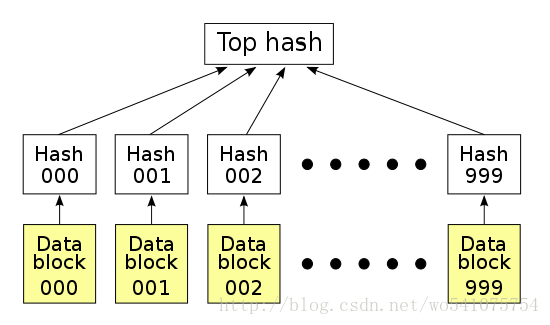
3、 Merkle Tree
Merkle Tree可以看做Hash List的泛化(Hash List可以看作一种特殊的Merkle Tree,即树高为2的多叉Merkle Tree)。
在最底层,和哈希列表一样,我们把数据分成小的数据块,有相应地哈希和它对应。但是往上走,并不是直接去运算根哈希,而是把相邻的两个哈希合并成一个字符串,然后运算这个字符串的哈希,这样每两个哈希就结婚生子,得到了一个”子哈希“。如果最底层的哈希总数是单数,那到最后必然出现一个单身哈希,这种情况就直接对它进行哈希运算,所以也能得到它的子哈希。于是往上推,依然是一样的方式,可以得到数目更少的新一级哈希,最终必然形成一棵倒挂的树,到了树根的这个位置,这一代就剩下一个根哈希了,我们把它叫做 Merkle Root[3]。
在p2p网络下载网络之前,先从可信的源获得文件的Merkle Tree树根。一旦获得了树根,就可以从其他从不可信的源获取Merkle tree。通过可信的树根来检查接受到的Merkle Tree。如果Merkle Tree是损坏的或者虚假的,就从其他源获得另一个Merkle Tree,直到获得一个与可信树根匹配的Merkle Tree。
Merkle Tree和Hash List的主要区别是,可以直接下载并立即验证Merkle Tree的一个分支。因为可以将文件切分成小的数据块,这样如果有一块数据损坏,仅仅重新下载这个数据块就行了。如果文件非常大,那么Merkle tree和Hash list都很到,但是Merkle tree可以一次下载一个分支,然后立即验证这个分支,如果分支验证通过,就可以下载数据了。而Hash list只有下载整个hash list才能验证。
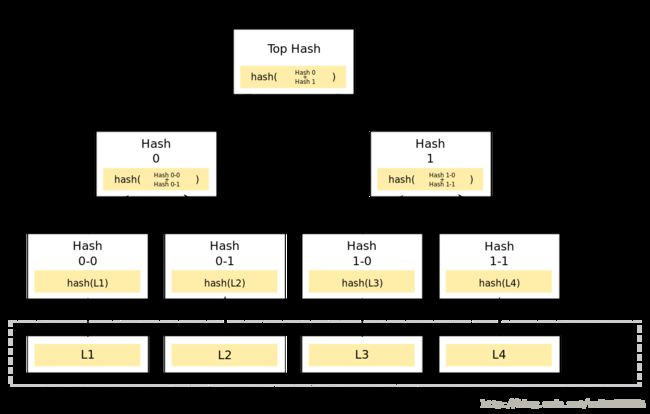
Merkle Tree的特点
- MT是一种树,大多数是二叉树,也可以多叉树,无论是几叉树,它都具有树结构的所有特点; phil 注: 注意不是二叉排序树
- Merkle Tree的叶子节点的value是数据集合的单元数据或者单元数据HASH。
- 非叶子节点的value是根据它下面所有的叶子节点值,然后按照Hash算法计算而得出的。[4][5]
通常,加密的hash方法像SHA-2和MD5用来做hash。但如果仅仅防止数据不是蓄意的损坏或篡改,可以改用一些安全性低但效率高的校验和算法,如CRC。
Second Preimage Attack: Merkle tree的树根并不表示树的深度,这可能会导致second-preimage attack,即攻击者创建一个具有相同Merkle树根的虚假文档。一个简单的解决方法在Certificate Transparency中定义:当计算叶节点的hash时,在hash数据前加0x00。当计算内部节点是,在前面加0x01。另外一些实现限制hash tree的根,通过在hash值前面加深度前缀。因此,前缀每一步会减少,只有当到达叶子时前缀依然为正,提取的hash链才被定义为有效。
Merkle Tree的操作
1、创建Merckle Tree
加入最底层有9个数据块。
step1:(红色线)对数据块做hash运算,Node0i = hash(Data0i), i=1,2,…,9
step2: (橙色线)相邻两个hash块串联,然后做hash运算,Node1((i+1)/2) = hash(Node0i+Node0(i+1)), i=1,3,5,7;对于i=9, Node1((i+1)/2) = hash(Node0i)
step3: (黄色线)重复step2
step4:(绿色线)重复step2
step5:(蓝色线)重复step2,生成Merkle Tree Root 
易得,创建Merkle Tree是O(n)复杂度(这里指O(n)次hash运算),n是数据块的大小。得到Merkle Tree的树高是log(n)+1。
2、检索数据块
为了更好理解,我们假设有A和B两台机器,A需要与B相同目录下有8个文件,文件分别是f1 f2 f3 ….f8。这个时候我们就可以通过Merkle Tree来进行快速比较。假设我们在文件创建的时候每个机器都构建了一个Merkle Tree。具体如下图: 
从上图可得知,叶子节点node7的value = hash(f1),是f1文件的HASH;而其父亲节点node3的value = hash(v7, v8),也就是其子节点node7 node8的值得HASH。就是这样表示一个层级运算关系。root节点的value其实是所有叶子节点的value的唯一特征。
假如A上的文件5与B上的不一样。我们怎么通过两个机器的merkle treee信息找到不相同的文件? 这个比较检索过程如下:
Step1. 首先比较v0是否相同,如果不同,检索其孩子node1和node2.
Step2. v1 相同,v2不同。检索node2的孩子node5 node6;
Step3. v5不同,v6相同,检索比较node5的孩子node 11 和node 12
Step4. v11不同,v12相同。node 11为叶子节点,获取其目录信息。
Step5. 检索比较完毕。
以上过程的理论复杂度是Log(N)。过程描述图如下:
3、更新,插入和删除
虽然网上有很多关于Merkle Tree的资料,但大部分没有涉及Merkle Tree的更新、插入和删除操作,讨论Merkle Tree的检索和遍历的比较多。我也是非常困惑,一种树结构的操作肯定不仅包括查找,也包括更新、插入和删除的啊。后来查到stackexchange上的一个问题,才稍微有点明白,原文见[6]。
对于Merkle Tree数据块的更新操作其实是很简单的,更新完数据块,然后接着更新其到树根路径上的Hash值就可以了,这样不会改变Merkle Tree的结构。但是,插入和删除操作肯定会改变Merkle Tree的结构,如下图,一种插入操作是这样的: 
插入数据块0后(考虑数据块的位置),Merkle Tree的结构是这样的: 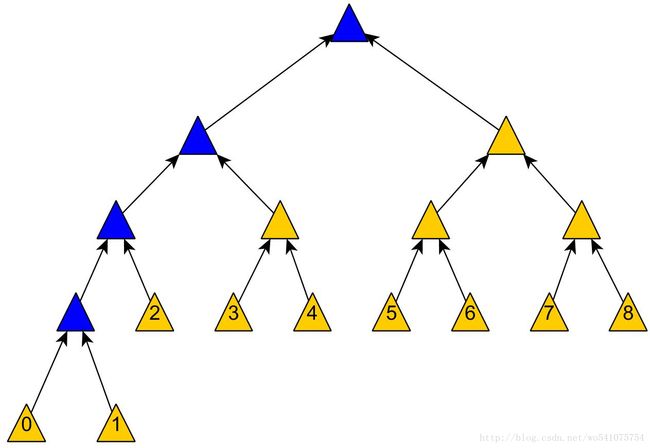
而[6]中的同学在考虑一种插入的算法,满足下面条件:
- re-hashing操作的次数控制在log(n)以内
- 数据块的校验在log(n)+1以内
- 除非原始树的n是偶数,插入数据后的树没有孤儿,并且如果有孤儿,那么孤儿是最后一个数据块
- 数据块的顺序保持一致
- 插入后的Merkle Tree保持平衡
然后上面的插入结果就会变成这样: 
根据[6]中回答者所说,Merkle Tree的插入和删除操作其实是一个工程上的问题,不同问题会有不同的插入方法。如果要确保树是平衡的或者是树高是log(n)的,可以用任何的标准的平衡二叉树的模式,如AVL树,红黑树,伸展树,2-3树等。这些平衡二叉树的更新模式可以在O(lgn)时间内完成插入操作,并且能保证树高是O(lgn)的。那么很容易可以看出更新所有的Merkle Hash可以在O((lgn)2)时间内完成(对于每个节点如要更新从它到树根O(lgn)个节点,而为了满足树高的要求需要更新O(lgn)个节点)。如果仔细分析的话,更新所有的hash实际上可以在O(lgn)时间内完成,因为要改变的所有节点都是相关联的,即他们要不是都在从某个叶节点到树根的一条路径上,或者这种情况相近。
[6]的回答者说实际上Merkle Tree的结构(是否平衡,树高限制多少)在大多数应用中并不重要,而且保持数据块的顺序也在大多数应用中也不需要。因此,可以根据具体应用的情况,设计自己的插入和删除操作。一个通用的Merkle Tree插入删除操作是没有意义的。