LeetCode(5) Longest Palindromic Substring
题目如下:
Given a string S, find the longest palindromic substring in S. You may assume that the maximum length of S is 1000, and there exists one unique longest palindromic substring.
分析如下:
1 时间复杂度为O(N³)的算法如果一个字符串从左向右写和从右向左写是一样的,这样的字符串就叫做palindromic string,如aba,或者abba。本题是这样的,给定输入一个字符串,要求输出一个子串,使得子串是最长的padromic string。
我的思路是从两边向中间扩展。先看2个例子。
以abba这样一个字符串为例来看,abba中,一共有偶数个字,第1位=倒数第1位,第2位=倒数第2位......第N位=倒数第N位
以aba这样一个字符串为例来看,aba中,一共有奇数个字符,排除掉正中间的那个字符后,第1位=倒数第1位......第N位=倒数第N位
所以,假设找到一个长度为len1的子串后,我们接下去测试它是否满足,第1位=倒数第1位,第2位=倒数第2位......第N位=倒数第N位,也就是说,去测试从头尾到中点,字符是否逐一对应相等。如果一直进行了[length/2]次后,对应字符都相等,即满足第i位=倒数第i位。那么这个子串必然是palindromic string。并且,很容易知道,无论这个字符串长度为奇数还是偶数,都是palindromic string,因为奇数位数的字符串相当于满足,第中间位=第中间位。
于是,现在问题转化为能不能找到一个子串,满足,第1位=倒数第1位(下文叫做候选子串)。如果有,就对剩下的字符做进一步的检查。这个问题可以用一个map(或者hash)来解决,把原字符串逐次扫描一遍,记录下每个字符出现过的下标为位置。例如,输入字符串为aba,那么可以这样来记录。伪码是:
vector
vector
map[a]=vec1;
map[b]=vec2.
这样,完成了第一步,构造好了一个map,储存了原字符串中,各个字符出现的位置了。
现在进行第二步,从头到尾再扫描一遍字符串,根据map中储存的位置,很容易找到候选子串了。
代码如下,时间复杂度是O(N³)
//
// Solution.h
// LeetCodeOJ_005_LongPalindrome
//
// Created by feliciafay on 11/26/13.
// Copyright (c) 2013 feliciafay. All rights reserved.
//
#ifndef LeetCodeOJ_005_LongPalindrome_Solution_h
#define LeetCodeOJ_005_LongPalindrome_Solution_h
#include
#include
#include 小结:
(1) 这个办法的时间复杂度为O(N²)比较高。
(2) 这里面有个坑。为了避免OJ出现一些极度长的字符串后出现溢出,我设定字符串非常大,于是假定用unsigned long long来表示字符串的下标,觉得这样必定够了吧。但是注意
其中第74行
if( ((long long)(tmp_index_tail-tmp_index_head)==-1) || (tmp_index_tail-tmp_index_head==0) ){和第58行
while( ((long long)(tmp_index_tail-tmp_index_head)>=1) && (s[tmp_index_tail]==s[tmp_index_head]) ) {2 时间复杂度为O(N²)的算法-动态规划
更简洁的做法,使用动态规划,这样可以把时间复杂度降到O(N²),空间复杂度也为O(N²)。做法如下:
首先,写出动态转移方程。
Define P[ i, j ] ← true iff the substring Si … Sj is a palindrome, otherwise false.
P[ i, j ] ← ( P[ i+1, j-1 ] and Si = Sj ) ,显然,如果一个子串是回文串,并且如果从它的左右两侧分别向外扩展的一位也相等,那么这个子串就可以从左右两侧分别向外扩展一位。
其中的base case是
P[ i, i ] ← true
P[ i, i+1 ] ← ( Si = Si+1 )
然后,看一个例子。
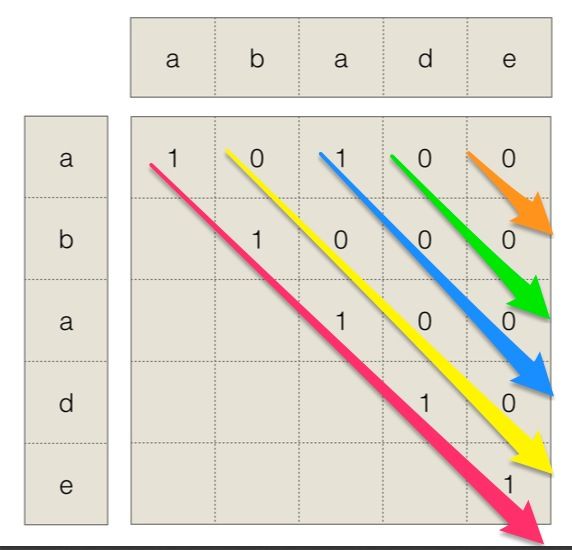
假设有个字符串是adade,现在要找到其中的最长回文子串。使用上面的动态转移方程,有如下的过程:
按照红箭头->黄箭头->蓝箭头->绿箭头->橙箭头的顺序依次填入矩阵,通过这个矩阵记录从i到j是否是一个回文串。
最后, 看code。
//动态规划算法
string longestPalindromeDP(string s) {
int n = s.length();
int longestBegin = 0;
int maxLen = 1;
bool table[1000][1000] = {false};
for (int i = 0; i < n; i++) {
table[i][i] = true;
}
for (int i = 0; i < n-1; i++) {
if (s[i] == s[i+1]) {
table[i][i+1] = true;
longestBegin = i;
maxLen = 2;
}
}
for (int len = 3; len <= n; len++) {
for (int i = 0; i < n-len+1; i++) {
int j = i+len-1;
if (s[i] == s[j] && table[i+1][j-1]) {
table[i][j] = true;
longestBegin = i;
maxLen = len;
}
}
}
return s.substr(longestBegin, maxLen);
}3 时间复杂度为O(N²)的算法-从中间向两边展开
回文字符串显然有个特征是沿着中心那个字符轴对称。比如aha沿着中间的h轴对称,a沿着中间的a轴对称。那么aa呢?沿着中间的空字符''轴对称。
所以对于长度为奇数的回文字符串,它沿着中心字符轴对称,对于长度为偶数的回文字符串,它沿着中心的空字符轴对称。
对于长度为N的候选字符串,我们需要在每一个可能的中心点进行检测以判断是否构成回文字符串,这样的中心点一共有2N-1个(2N-1=N-1 + N)。
检测的具体办法是,从中心开始向两端展开,观察两端的字符是否相同。代码如下:
//从中间向两边展开
string expandAroundCenter(string s, int c1, int c2) {
int l = c1, r = c2;
int n = s.length();
while (l >= 0 && r <= n-1 && s[l] == s[r]) {
l--;
r++;
}
return s.substr(l+1, r-l-1);
}
string longestPalindromeSimple(string s) {
int n = s.length();
if (n == 0) return "";
string longest = s.substr(0, 1); // a single char itself is a palindrome
for (int i = 0; i < n-1; i++) {
string p1 = expandAroundCenter(s, i, i); //长度为奇数的候选回文字符串
if (p1.length() > longest.length())
longest = p1;
string p2 = expandAroundCenter(s, i, i+1);//长度为偶数的候选回文字符串
if (p2.length() > longest.length())
longest = p2;
}
return longest;
}4 时间复杂度为O(N)的算法
在这里看到了更更简洁的做法,可以把时间复杂度降到O(N).具体做法原文说得很清楚,有图有例,可以仔细读读。
这里我只想写写,为什么这个算法的时间复杂度是O(N)而不是O(N²)。从代码中看,for循环中还有个while,在2层嵌套的循环中,似乎应该是O(N²)的时间复杂度。
// Transform S into T.
// For example, S = "abba", T = "^#a#b#b#a#$".
// ^ and $ signs are sentinels appended to each end to avoid bounds checking
string preProcess(string s) {
int n = s.length();
if (n == 0) return "^$";
string ret = "^";
for (int i = 0; i < n; i++)
ret += "#" + s.substr(i, 1);
ret += "#$";
return ret;
}
string longestPalindrome(string s) {
string T = preProcess(s);
int n = T.length();
int *P = new int[n];
int C = 0, R = 0;
for (int i = 1; i < n-1; i++) {
int i_mirror = 2*C-i; // equals to i' = C - (i-C)
P[i] = (R > i) ? min(R-i, P[i_mirror]) : 0;
// Attempt to expand palindrome centered at i
while (T[i + 1 + P[i]] == T[i - 1 - P[i]])
P[i]++;
// If palindrome centered at i expand past R,
// adjust center based on expanded palindrome.
if (i + P[i] > R) {
C = i;
R = i + P[i];
}
}
// Find the maximum element in P.
int maxLen = 0;
int centerIndex = 0;
for (int i = 1; i < n-1; i++) {
if (P[i] > maxLen) {
maxLen = P[i];
centerIndex = i;
}
}
delete[] P;
return s.substr((centerIndex - 1 - maxLen)/2, maxLen);
}时间复杂度为什么是O(N)而不是O(N²)呢?
假设真的是O(N²),那么在每次外层的for循环进行的时候(一共n步),对于for的每一步,内层的while循环要进行O(N)次。而这是不可能。因为p[i]和R是有相互影响的。while要么就只走一步,就到了退出条件了。要么就走很多很步。如果while走了很多步,多到一定程度,会更新R的值,使得R的值增大。而一旦R变大了,下一次进行for循环的时候,while条件直接就退出了。
更加理论的分析是amortized analysis,可以参考CLRS,我暂时还没有去看那一章。。。。。。
5 参考资料
1. Longest Palindromic Substring Part I
2. Longest Palindromic Substring Part II
3. 最长回文子串
update: 2014-12-15
思路和第3个解法一样,但是写得不够简洁
class Solution {
public:
string palindrome_length(string s, int center, bool is_center_included ) {
if (is_center_included) {
int i = center, j = center;
while (i >=0 && j < s.length() && s[i] == s[j]) {
i--;
j++;
}
return s.substr(i + 1, j - i -1);
} else {
//下标为center的点的右侧作为中心。
int i = center, j = center + 1;
while (i >=0 && j < s.length() && s[i] == s[j]) {
i--;
j++;
}
return s.substr(i + 1, j - i - 1);
}
}
string longestPalindrome(string s) {
if (s.length() <= 1) return s;
string result = "";
string temp = "";
for (int i = 0; i < s.length(); ++i) {
temp = palindrome_length(s, i, true);
if (temp.length() > result.length())
result = temp;
if (i == s.length() - 1) continue;
temp = palindrome_length(s, i, false);
if (temp.length() > result.length())
result = temp;
}
return result;
}
};