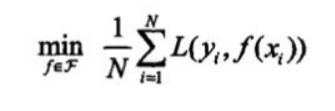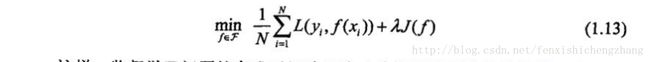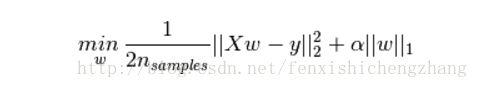LinearRegression,Ridge,RidgeCV,Lasso线性回归模型简单使用
一、线性回归
LinearRegression：使用经验风险最小化=损失函数（平方损失）
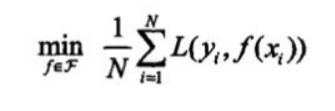
>>> from sklearn import linear_model #导入模块
>>> reg = linear_model.LinearRegression() #导入模型
>>> reg.fit ([[0, 0], [1, 1], [2, 2]], [0, 1, 2]) #模型训练
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False) # copy_X:是否备份，fit_intercept:是否保存截距，n_jobs:?
normalize:是否标准化
>>> reg.coef_ # 训练后模型权重（特征个数无变化）
array([ 0.5, 0.5])
>>> reg.intercept_ # 训练后模型截距
1.1102230246251565e-16
>>> reg.predict([[2,5]]) # 训练后模型预测
array([ 3.5])
>>> reg.normalize # 训练中是否标准化
False
>>> reg.get_params # 获取模型训练前设置的参数
True, fit_intercept=True, n_jobs=1, normalize=False)> 二、岭回归
Ridge/RidgeCV：使用结构风险最小化=损失函数（平方损失）+正则化（L2范数）
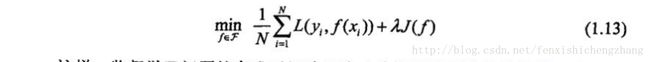
Ridge:固定阿尔法，求出最佳w，阿尔法与w的范数成反比
>>> from sklearn import linear_model
>>> reg = linear_model.Ridge (alpha = .5) #导入模型并传入一个数
>>> reg.fit ([[0, 0], [0, 0], [1, 1]], [0, .1, 1]) #训练模型
Ridge(alpha=0.5, copy_X=True, fit_intercept=True, max_iter=None,
normalize=False, random_state=None, solver='auto', tol=0.001)
>>> reg.coef_ #获取权重w1...wn
array([ 0.34545455, 0.34545455])
>>> reg.intercept_ #获取截距w0
0.13636...
>>> reg.set_params(alpha=0.6)#重新设置参数alpha=0.6
Ridge(alpha=0.6, copy_X=True, fit_intercept=True, max_iter=None,
normalize=False, random_state=None, solver='auto', tol=0.001)
#tol收敛精度
>>> reg.fit ([[0, 0], [0, 0], [1, 1]], [0, .1, 1])#重新训练模型
Ridge(alpha=0.6, copy_X=True, fit_intercept=True, max_iter=None,
normalize=False, random_state=None, solver='auto', tol=0.001)
>>> reg.coef_
array([ 0.32758621, 0.32758621])RidgeCV:多个阿尔法，得出多个对应最佳的w,然后得到最佳的w及对应的阿尔法
>>> from sklearn import linear_model #导入模型
>>> reg = linear_model.RidgeCV(alphas=[0.1, 1.0, 10.0])#导入模型传入数组
>>> reg.fit([[0, 0], [0, 0], [1, 1]], [0, .1, 1]) #训练模型
RidgeCV(alphas=[0.1, 1.0, 10.0], cv=None, fit_intercept=True, scoring=None,normalize=False)
>>> reg.alpha_ #获取权重
0.1三、套索（适合稀疏数据集）
Lasso：使用结构风险最小化=损失函数（平方损失）+正则化（L1范数）
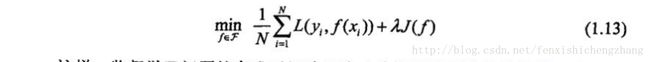
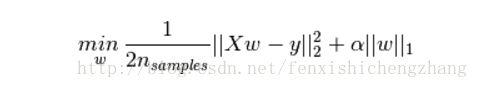
>>> from sklearn import linear_model # 导入模型参数
>>> reg = linear_model.Lasso(alpha = 0.1)#导入模型传入参数alpha=0.1
>>> reg.fit([[0, 0], [1, 1]], [0, 1])#训练数据
Lasso(alpha=0.1, copy_X=True, fit_intercept=True, max_iter=1000,normalize=False, positive=False, precompute=False, random_state=None,selection='cyclic', tol=0.0001, warm_start=False)
#max_iter：迭代次数，tol:收敛精度
>>> reg.predict([[1, 1]])#模型预测
array([ 0.8])