文法和正规式

1、终结符和非终结符

　　终结符：不能够单独的出现在推导式左边的符号，是一个原子量，不能够再分解，是最终状态，不能够转换成其他状态，也不能够用其它的几个量进行代替，不能够再推导出其它符号。如a->b就是错的，因为终结符不能在左边。

　　非终结符：可以理解为一个可以拆分的元素。

　　一般用大写的字符代表非终结符，小写字母代表终结符。

2、文法

　　　　　　　　　　　　　　　　　

　　其中，Vn是非终结符集合；Vt是终结符集合；P是推导式集合；S就是开始符。

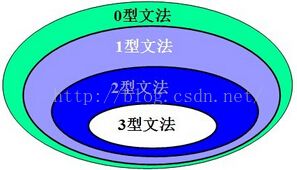
　　（1）0型文法

　　　　设G={VT,VN,S,P}，如果它的每个产生式α→β是这样一种结构：α∈(VT∪VN)* 且至少含有一个非终结符，而β∈(VT∪VN)*，则G是一个0型文法。0型文法也称短语文法。一个非常重要的理论结果是：0型文法的能力相当于图灵机(Turing)。或者说，任何0型文语言都是递归可枚举的，反之，递归可枚举集必定是一个0型语言。0型文法是这几类文法中限制最少的一个，所以一般见到的至少是0型文法。

　　　　0型文法的本意其实就是不能让在左边的符号不能够全部为终结符，即a->b这种形式不能出现，而Ab->c是可以的。

　　（2）1型文法

　　　　1型文法又称为上下文有关文法，此文法对应于线性有界自动机，它是在0型文法的基础上增加了一条对于每一个a->b，都存在|a|<=|b|，这里的|b|表示的是b的长度，而不是绝对值。即由Ab->B不属于1型文法，而A->Bba则属于1型文法。

　　　　特例：A->空也属于1型文法。

　　（3）2型文法

　　　　2型文法也叫作上下文无关文法，它对应于下推自动机。2型文法是在1型文法的基础上再满足：每一个a->b都有a是非终结符，如A->Ba符合2型文法要求。

　　　　如Ab->Bab不是2型文法，因为Ab不是非终结符。

　　（4）3型文法

　　　　3型文法也叫作正规文法，它对应于有限状态自动机，它是在2型文法的基础上满足：A->a|aB（右线性）或A->a|Ba（左线性）。如果有A->a,A->aB,B->a,B->cB则符合3型文法的要求。但是A->ab,A->aB,B->a,B->cB或A->a,A->Ba,B->a,B->cB则不符合3型文法的要求。

　　　　也就是说，不能够推导出两个终结符，而且左线性和右线性只能使用一种，不能够同时出现。

　　　　　　　　　

　　　　总结：0型文法要求左边不能全部为终结符，满足；1型文法要求左边长度不大于右边长度，满足；2型文法要求左边全部为非终结符；G文法中左线性和右线性同时存在，所以不满足3型文法。

　　　　四种文法的关系为：

　　　　　　　　　　　　　　　

　　（５）文法的优点：

　　　　（1）文法为语言给出了精确的、易于理解的语法说明。

　　　　（2）对于某些文法类，可以自动产生高效的分析器。额外的好处是，分析器的自动构造过程可以揭示出语法的二义性和其他不属于该文法类的语法结构，这些问题在语言及其编译器的最初设计阶段很可能没有发现。

　　　　（3）设计得漂亮的文法可以给程序定义一些语法子结构，这些结构对于把源程序翻译成为正确的目标代码和错误诊断都是有用的。把以文法为基础的翻译描述变换成为相应程序的工具也是存在的。

　　　　（4）语言也是逐渐完善的，需要补充新的结构并完成新增的任务。如果存在以文法为基础的语言的实现，这些新结构的加入就更方便。

3、正规式

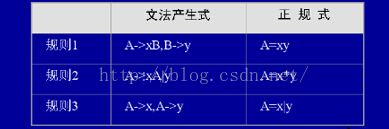
　　正规式，就是我们之前说过的3型文法，每一个正规式都对应一个正规文法，他们之间是能够互相转换的。正规式与文法之间的转换为：

　　　　　　　　　　　　

因为A->xA|y，中可能会产生递归的，当A推出y的时候，就能结束了，所以A=x*y。