哈夫曼树及其应用
哈夫曼树树,也称最优二叉树,是指对于一组带有确定权值的叶结点,构造的具有最小带权路径长度的二叉树。二叉树的路径长度是指由根结点到所有叶结点的路径之和。设二叉树具有n个带权值的叶结点,那么从根结点到各个叶结点的路径长度和相应结点权值的乘积之和叫做二叉树的带权路劲长度。记为:
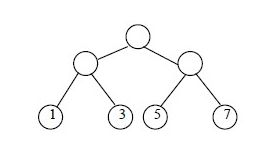
其中Wk为第k个叶结点的权值,Lk为第k个叶结点的路径长度。如图所示的二叉树,它的带权路径长度为WPL = 1 x 2 + 3 x 2 + 5 x2 + 7 x 2 = 32 ;
哈夫曼树种权值越大的结点越靠近根结点,而权值越小的结点则越远离结点。根据这一特点可以得到哈夫曼树的构造方法,构造方法如下:
(1)由给定的n个权值(W1 ,W2, W3, ... ,Wn)构造n棵只有一个叶结点的二叉树,从而得到二叉树的集合F = {T1, T2,..., Tn};
(2)在F张选取根结点的权值最小和次小的两颗二叉树分别最为左右子树构造一颗新的二叉树,这棵新的二叉树的根节点的权值为左右子树结点的权值之和;
(3)在集合F中删除为左右子树的两个二叉树,并将新建立的二叉树加入到集合F中;
(4)重复(2),(3)步骤,当F中只剩下一棵二叉树,即为我们所要建立的哈夫曼树;
由哈夫曼树的构造方法可知,哈夫曼树具有以下特点:
(1)满二叉树不一定是哈夫曼树树;
(2)哈夫曼树不存在度数为1的结点;
(3)根据(2)可得,根据二叉树的性质得n个叶结点的二叉树有n-1个度数为2的结点,所以整棵二叉树共有2n-1个结点;
哈夫曼树的构造:
#include
#include
#define MAXVALUE 1000 //定义最大权值;
#define MAXLEAF 30 //叶结点的最多个数
#define MAXNODE MAXLEAF*2-1 //哈夫曼树的结点个数
typedef struct
{
int weight;
int parent;
int lchild;
int rchild;
}HNodeType;
/*-----------------------------------
函数功能:构造哈夫曼树
函数参数:哈夫曼树HuffNode
叶子结点的个数n
-----------------------------------*/
void Huffman(HNodeType HuffNode[],int n)
{
int m1,m2,x1,x2,i,j;
//初始化
for(i = 0;i < 2*n-1;i++)
{
HuffNode[i].weight = 0;
HuffNode[i].parent = -1;
HuffNode[i].lchild = -1;
HuffNode[i].rchild = -1;
}
//输入结点的权重
printf("Input the weight of node:");
for(i = 0;i < n;i++)
{
scanf("%d",&HuffNode[i].weight);
}
//构造哈夫曼树n-1个非叶子结点
for(i = 0;i < n-1;i++)
{
//m1,m2分别保存F中权值最小的权重
m1 = m2 = MAXVALUE;
//x1,x2保存两个权值最小的结点的下标
x1 = x2 = 0;
for(j = 0;j < n+i;j++)
{
if(HuffNode[j].weight < m1 && HuffNode[j].parent == -1)
{
m2 = m1;
x2 = x1;
m1 = HuffNode[j].weight;
x1 = j;
}
else if(HuffNode[j].weight < m2 && HuffNode[j].parent == -1)
{
m2 = HuffNode[j].weight;
x2 = j;
}
}
//合并为一棵子树
HuffNode[x1].parent = n+i;
HuffNode[x2].parent = n+i;
HuffNode[n+i].weight = HuffNode[x1].weight+ HuffNode[x2].weight;
HuffNode[n+i].lchild = x1;
HuffNode[n+i].rchild = x2;
}
} (1)哈夫曼编码
#define MAXBIT 10 //哈夫曼编码的最大长度
typedef struct
{
int bit[MAXBIT]; //保存哈夫曼编码
int start; //编码存放在从start+1到MAXBIT
}HCodeType;
/*----------------------------------
*函数功能:哈夫曼编码
----------------------------------*/
void HuffmanCode(HNodeType HuffNode[],int n)
{
HCodeType HuffCode[MAXLEAF],cd;
int i,j,c,p;
//求每一个叶子结点的哈夫曼编码
for(i = 0;i < n;i++)
{
cd.start = MAXBIT-1;
c = i;
p = HuffNode[c].parent;
//从叶子一直往上
while(p != -1)
{
if(HuffNode[p].lchild == c)
cd.bit[cd.start] = 0;
else
cd.bit[cd.start] = 1;
cd.start--;
c = p;
p = HuffNode[c].parent;
}
//保存哈夫曼编码
for(j = cd.start+1;j < MAXBIT;j++)
{
HuffCode[i].bit[j] = cd.bit[j];
}
HuffCode[i].start = cd.start;
}
//输出
for(i = 0; i < n;i++)
{
for(j = HuffCode[i].start+1;j < MAXBIT;j++)
{
printf("%d",HuffCode[i].bit[j]);
}
printf("\n");
}
}
/*----------------------------------
函数功能:对哈夫曼编码进行解码
函数参数:哈夫曼树HuffNode
待解码的字符串code
叶子结点个数n
---------------------------------*/
void decoding(HNodeType HuffNode[],char code[],int n)
{
char *p = code;
//n个叶结点的哈夫曼树总共有2n-1个结点,根结点的位置为2*n-2
int i,root = 2*n-2;
while(*p != '\0')
{
i = root;
//从根部开始遍历
while(HuffNode[i].lchild != -1 && HuffNode[i].rchild != -1)
{
if(*p == '0')
i = HuffNode[i].lchild;
else
i = HuffNode[i].rchild;
p++;
}
printf("%3d",HuffNode[i].weight);
}
printf("\n");
}(2)判断比较
例如,如果要编制一个将百分之转换为五级分制的程序。通常情况下只需要条件语句便可完成。如:
if (a<60) b=”bad”;
else if (a<70) b=”pass”
else if (a<80) b=”general”
else if (a<90) b=”good”
else b=”excellent”;如果数据量小的话还好说,可是当数据量大的时候,效率就不会很高这个时候我们就可以通过哈夫曼树来进行判定,把出现频率高的分数段赋予更大的权值,那么比较的时候就会越快。
上述哈夫曼树为静态哈夫曼树,静态哈夫曼编码的最大的缺点就是需要对数据进行两次扫瞄,第一次统计原始字符中各字符出现的频率,第二遍进行编码。为了解决这个问题Faller提出了自适应哈夫曼编码,即动态哈夫曼树,也就是说,对第t+1个字符编码是根据原始数据中前t个字符得到的哈夫曼树来进行的.
在构造动态哈夫曼编码树的过程中需要遵循两条重要的规则
(1)权值大的结点,结点编号也较大。
(2)父结点的节点编号总是大于子节点编号
这两条规则称为兄弟属性。
静态哈夫曼方法的最大缺点就是
它需要对原始数据进行两遍扫描
:
第一
遍统计原始数据中各字符出现的频
率,利用得到的频率值创建哈夫曼树
并将树的有关信息保存起来,便于解
压时使用
;
第二遍则根据前面得到的哈
夫曼树对原始数据进行编码,并将编
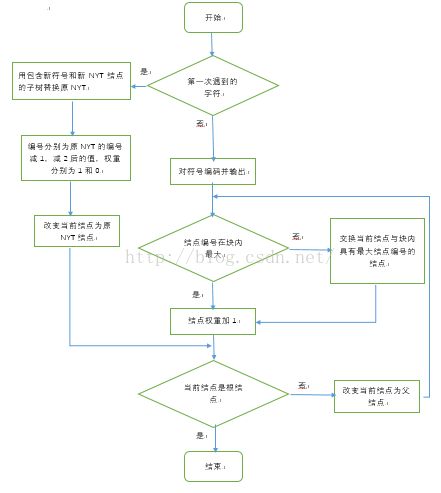
对一个输入符号进行哈夫曼编码并更新编码的流程图如图所示:
具体实现:
#include
#include
struct Node
{
unsigned char letter; //字符
int weight; //权重
int order; //编号
struct Node *parent; //父结点
struct Node *lchild; //左孩子
struct Node *rchild; //右孩子
struct Node *front; //前指针
struct Node *after; //后指针
}*Root;
struct LeafNode
{
struct LeafNode *next; //叶结点链的next指针
struct Node *charnode;
}*Leaf,*Weight; //叶子链,权重链的头指针
void compression(char string[]);
void decompression(void);
void update(struct Node *);
void addchar(unsigned char);
void producecode(struct Node *);
void InsertWeight(struct Node *Temp);
/**************************************
函数功能:初始化
**************************************/
void initial(void)
{
Root = (struct Node *)malloc(sizeof(struct Node));
Root->parent = NULL;
Root->lchild = Root->rchild = NULL;
Root->front = Root->after = NULL;
Root->weight = 0;
Root->letter = 0;
Root->order = 1000;
Leaf = (struct LeafNode *)malloc(sizeof(struct LeafNode));
Weight = (struct LeafNode *)malloc(sizeof(struct LeafNode));
Leaf->charnode = Root;
Weight->charnode = NULL;
Weight->next = Leaf->next = NULL;
}
/**************************************
函数功能:添加字符,即叶结点
函数参数:新的字符letter
**************************************/
void addchar(unsigned char letter)
{
struct Node *Tempa, *Tempb,*Tempc;
struct LeafNode *q;
Tempa = Leaf->charnode;
Tempb = (struct Node *)malloc(sizeof(struct Node));
Tempc = (struct Node *)malloc(sizeof(struct Node));
Tempb->parent = Tempc->parent = Tempa;
Tempb->lchild = Tempc->lchild = NULL;
Tempb->rchild = Tempc->rchild = NULL;
Tempb->front = Tempc->front = NULL;
Tempb->after = Tempc->after = NULL;
Tempb->letter = 0;
Tempc->letter = letter;
Tempb->weight = 0;
Tempc->weight = 1;
Tempb->order = Tempa->order - 2;
Tempc->order = Tempa->order - 1;
Tempa->lchild = Tempb;
Tempa->rchild = Tempc;
//将新叶子结点插入到叶子链中
q = (struct LeafNode *)malloc(sizeof(struct LeafNode));
q->charnode = Tempc;
Leaf->charnode = Tempb;
q->next = Leaf->next;
Leaf->next = q;
InsertWeight(Tempc);
}
void producecode(struct Node *Pointer)
{
char code[50],count = 0,i;
if(Pointer != Root)
{
while(Pointer != Root)
{
if(Pointer == (Pointer->parent->lchild))
code[count] = '0';
else
code[count] = '1';
count++;
// printf("权值:%3d;\n",Pointer->weight);
Pointer = Pointer->parent;
}
}
for(i = count -1;i >= 0;i--)
{
printf("%c",code[i]);
}
printf("\n");
}
/**************************************
函数功能:插入权值
函数参数:结点Temp
**************************************/
void InsertWeight(struct Node *Temp)
{
struct LeafNode *p,*q;
char flag = 0;
struct Node *Tempa;
p = Weight;
Temp->after = Temp->front = NULL;
//查找权重链中与插入结点权重相等的结点
while(p->next != NULL)
{
if(p->next->charnode->weight == Temp->weight)
{
flag = 1;
break;
}
else
p = p->next;
}
//没找到,直接插入到权重链尾部
if(!flag)
{
q = (struct LeafNode *)malloc(sizeof(struct LeafNode));
p->next = q;
q->next = NULL;
q->charnode = Temp;
}
else
{ //按照序号由大到小插入
Tempa = p->next->charnode;
//需要插入的结点的序号最大
if(Temp->order >= Tempa->order)
{
Temp->after = Tempa;
Tempa->front = Temp;
p->next->charnode = Temp;
}
else
{
while(Tempa->after != NULL)
{
if(Tempa->after->order < Temp->order)
break;
else
Tempa = Tempa->after;
}
Temp->after = Tempa->after;
Temp->front = Tempa;
Tempa->after = Temp;
if(Temp->after != NULL)
Temp->after->front = Temp;
}
}
}
/**************************************
函数功能:调整哈夫曼树
函数参数:结点Temp
**************************************/
void update(struct Node *Temp)
{
struct Node *Tempa,*Tempc,*Pointer;
struct LeafNode *p,*q,*b;
unsigned char Letter;
//当Temp不为Root时,即根节点时
while(Temp != Root)
{
//当Temp->weight
if(Temp->weight)
{
p = Weight;
//在权重链中找到相同权重的结点
while(p->next->charnode->weight != Temp->weight )
p = p->next;
//如果Temp->front == NULL,那么Temp就是相同权重的结点中序号最大的结点
if(Temp->front != NULL)
{
Tempa = Temp;
//找到序号最大的结点
while(Temp->front != NULL)
Temp = Temp->front;
// if(Temp != Tempa->parent)
// {
//交换左孩子
Pointer = Temp->lchild;
if(Pointer != NULL)
Pointer->parent = Tempa;
Temp->lchild = Tempa->lchild;
if(Temp->lchild != NULL)
Temp->lchild->parent = Temp;
Tempa->lchild = Pointer;
//交换右孩子
Pointer = Temp->rchild;
if(Pointer != NULL)
Pointer->parent = Tempa;
Temp->rchild = Tempa->rchild;
if(Temp->rchild != NULL)
Temp->rchild->parent = Temp;
Tempa->rchild = Pointer;
//交换字符,但是不交换序号和权重,因为权重一样
Letter = Temp->letter;
Temp->letter = Tempa->letter;
Tempa->letter = Letter;
//如果交换的是叶结点的话,需要更新叶子链,同一个结点,序号没变,内容发生了改变
if((Tempa->lchild == NULL)&&(Tempa->rchild == NULL))
{
b = Leaf;
while(b != NULL)
{
if(b->charnode == Temp)
{
b->charnode = Tempa;
break;
}
else
b = b->next;
}
}
if((Temp->lchild == NULL) && (Temp->rchild == NULL))
{
b = Leaf;
while(b != NULL)
{
if(b->charnode == Tempa)
{
b->charnode = Temp;
break;
}
else
b = b->next;
}
}
// }
}
//更新权重链,取下序号最大的结点Temp,后面重新插入以更新
p->next->charnode = Temp->after;
if(Temp->after == NULL)
{
q = p->next;
p->next = q->next;
free(q);
}
else
Temp->after->front = NULL;
}
Temp->weight++;
Temp->after = Temp->front = NULL;
//重新插入更新
InsertWeight(Temp);
Temp = Temp->parent;
}
}
void compression(char string[])
{
struct LeafNode *p;
int i = 0;
int flag;
initial(); //初始化哈夫曼树
while(string[i] != '\0')
{
flag = 0;
p = Leaf->next; //在叶子链中进行查找
while(p != NULL)
{
//如果存在于叶子链中
if(p->charnode->letter == string[i])
{
flag = 1;
break;
}
else
p = p->next;
}
//如果不存在于叶子链中
if(!flag)
{
addchar(string[i]); //添加此字符到哈夫曼树中
update(Leaf->charnode->parent); //更新哈夫曼树,从插入结点的父结点开始
producecode(Leaf->charnode); //产生此字符的编码
}
else
{
update(p->charnode);
producecode(p->charnode);
}
i++;
}
}
int main()
{
char string[20];
scanf("%s",string);
compression(string);
return 0;
}