递推算法
递推概念
什么是递推
所谓递推,是指从已知的初始条件出发,依据某种递推关系,逐次推出所要求的各中间结果及最后结果。其中初始条件或是问题本身已经给定,或是通过对问题的分析与化简后确定。
从已知条件出发逐步推到问题结果,此种方法叫顺推。
从问题出发逐步推到已知条件,此种方法叫逆推。
无论顺推还是逆推,其关键是要找到递推式。这种处理问题的方法能使复杂运算化为若干步重复的简单运算,充分发挥出计算机擅长于重复处理的特点。
递推法是一种重要的数学方法,在数学的各个领域中都有广泛的运用,也是计算机用于数值计算的一个重要算法。
递推算法的首要问题是得到相邻的数据项间的关系(即递推关系)。递推算法避开了求通项公式的麻烦,把一个复杂的问题的求解,分解成了连续的若干步简单运算。一般说来,可以将递推算法看成是一种特殊的迭代算法。
递推的特点
可用递推算法求解的题目一般有以下两个特点:
1、问题可以划分成多个状态;
2、除初始状态外,其它各个状态都可以用固定的递推关系式来表示。
在我们实际解题中,题目不会直接给出递推关系式,而是需要通过分析各种状态,找出递推关系式。
【例1】数字三角形。
如下所示为一个数字三角形。请编一个程序计算从顶到底的某处的一条路径,使该路径所经过的数字总和最大。只要求输出总和。

1、 一步可沿左斜线向下或右斜线向下走;
2、 三角形行数小于等于100;
3、 三角形中的数字为0,1,…,99;
测试数据通过键盘逐行输入,如上例数据应以如下所示格式输入:
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
【算法分析】
此题解法有多种,从递推的思想出发,设想,当从顶层沿某条路径走到第i层向第i+1层前进时,我们的选择一定是沿其下两条可行路径中最大数字的方向前进,为此,我们可以采用倒推的手法,设a[i][j]存放从i,j 出发到达n层的最大值,则a[i][j]=max{a[i][j]+a[i+1][j],a[i][j]+a[i+1][j+1]},a[1][1] 即为所求的数字总和的最大值。
//【参考程序】
#include
using namespace std;
int main(){
int n,i,j,a[101][101];
cin>>n;
for (i=1;i<=n;i++)
for (j=1;j<=i;j++)
cin>>a[i][j]; //输入数字三角形的值
for (i=n-1;i>=1;i--)
for (j=1;j<=i;j++)
{
if (a[i+1][j]>=a[i+1][j+1]) a[i][j]+=a[i+1][j]; //路径选择
else a[i][j]+=a[i+1][j+1];
}
cout< 思考
如果要输出最大和的路径该怎么处理呢?
【例2】 骨牌问题
有2 × n的一个长方形方格,用一个1 × 2的骨牌铺满方格。
编写一个程序,试对给出的任意一个n(n>0), 输出铺法总数。
【算法分析】
(1)面对上述问题,如果思考方法不恰当,要想获得问题的解答是相当困难的。可以用递推方法归纳出问题解的一般规律。
(2)当n=1时,只能是一种铺法,铺法总数有示为x1=1。
(3)当n=2时:骨牌可以两个并列竖排,也可以并列横排,再无其他方法,如下左图所示,因此,铺法总数表示为x2=2;
![]()
(4)当n=3时:骨牌可以全部竖排,也可以认为在方格中已经有一个竖排骨牌,则需要在方格中排列两个横排骨牌(无重复方法),若已经在方格中排列两个横排骨牌,则必须在方格中排列一个竖排骨牌。如上右图,再无其他排列方法,因此铺法总数表示为x3=3。
由此可以看出,当n=3时的排列骨牌的方法数是n=1和n=2排列方法数的和。
(5)推出一般规律:对一般的n,要求xn可以这样来考虑,若第一个骨牌是竖排列放置,剩下有n-1个骨牌需要排列,这时排列方法数为xn-1;若第一个骨牌是横排列,整个方格至少有2个骨牌是横排列(1*2骨牌),因此剩下n-2个骨牌需要排列,这是骨牌排列方法数为xn-2。从第一骨牌排列方法考虑,只有这两种可能,所以有:
xn=xn-1+xn-2 (n>2)
x1=1
x2=2
xn=xn-1+xn-2就是问题求解的递推公式。任给n都可以从中获得解答。例如n=5,
x3=x2+x1=3
x4=x3+x2=5
x5=x4+x3=8
//下面是输入n,输出x1~xn的c++程序:
int main(){
int n,i,j,a[101];
cout<<"input n:"; //输入骨牌数
cin>>n;
a[1]=1;a[2]=2;
cout<<"x[1]="<
2.长方形和正方形的个数之和s
宽为1的长方形和正方形有m个,宽为2的长方形和正方形有m-1个,┉,宽为m的长方形和正方形有1个;
长为1的长方形和正方形有n个,长为2的长方形和正方形有n-1个,┉,长为n的长方形和正方形有1个;
根据乘法原理
s=(1+2+┉┉+n)×( 1+2+┉┉+m)=

3.长宽不等的长方形个数s2
显然,s2=s-s1 =

//由此得出算法:
int main(){
int n,m;
cin>>m>>n;
int m1=m,n1=n,s1=m*n; //计算正方形的个数s1
while (m1!=0&&n1!=0)
{
m1--;n1--;
s1+=m1*n1;
}
int s2=((m+1)*(n+1)*m*n)/4-s1; // 计算长方形的个数s2
cout<
小结
一.递推的概念与基本思想:
给定一个数的序列H0,H1,…,Hn,…若存在整数n0,使当n>n0时,可以用等号(或大于号、小于号)将Hn与其前面的某些项Hi(0 二.解决递推问题的一般步骤
1.建立递推关系式;(问题可以划分成多个状态;除初始状态外,其它各个状态都可以用固定的递推关系式来表示。实际解题中,题目不会直接给出递推关系式,而是需要通过分析各种状态,找出递推关系式。)
2.确定边界条件;
3.递推求解;
三.递推的形式递推分顺推法和倒推法两种形式。
1、顺推法: 从已知条件出发,逐步推出要解决的问题。
2、逆推法:从问题出发,逐步推到已知条件。

练习
采用具体化、特殊化的方法寻找规律
平面上n条直线,任两条不平行,任三条不共点,问这n条直线把这平面划分为多少个部分?
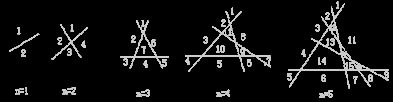
输入:2
输出:4
【例4】昆虫繁殖
【问题描述】
科学家在热带森林中发现了一种特殊的昆虫,这种昆虫的繁殖能力很强。每对成虫过x个月产y对卵,每对卵要过两个月长成成虫。假设每个成虫不死,第一个月只有一对成虫,且卵长成成虫后的第一个月不产卵(过X个月产卵),问过Z个月以后,共有成虫多少对?0= 【输入格式】
x,y,z的数值
【输出格式】
过Z个月以后,共有成虫对数
【输入样例】
1 2 8
【输出样例】
37
//【参考程序】
int main(){
long long a[101]={0},b[101]={0},i,j,x,y,z;
cin>>x>>y>>z;
for(i=1;i<=x;i++){a[i]=1;b[i]=0;}
for(i=x+1;i<=z+1;i++) //因为要统计到第z个月后,所以要for到z+1
{
b[i]=y*a[i-x];
a[i]=a[i-1]+b[i-2];
}
cout<
【例5】位数问题
【问题描述】
在所有的N位数中,有多少个数中有偶数个数字3?由于结果可能很大,你只需要输出这个答案对12345取余的值。
【输入格式】
读入一个数N
【输出格式】
输出有多少个数中有偶数个数字3。
【输入样例】
2
【输出样例】
73
【数据规模】
1<=N<=1000
【样例说明】
在所有的2位数字,包含0个3的数有72个,包含2个3的数有1个,共73个
【算法分析】
方法一:排列组合(但需要运用动态规划)。
可以列出公式,在n个格子中放x个3(其中x为偶数,包括0).。
c(n,x)*9 ^ (n-x) - c(n-1,x)*9 ^ (n-x-1) 含义为在n个格子中取x个3,且不考虑第一位的特殊情况为c(n,x)*9^(n-x)。
而第一位为0的情况,为c(n-1,x)*9^(n-x-1),两者减下,就为答案。
方法二:递推
考虑这种题目,一般来说都是从第i-1位推导第i位,且当前位是取偶数还是取奇数的。
恍然大悟.可以用f[i][0]表示前i位取偶数个3有几种情况,f[i][1]表示前i位取奇数个3有几种情况。
则状态转移方程可以表示为:
f[i][0]=f[i-1][0]*9+f[i-1][1];f[i][1]=f[i-1][0]+f[i-1][1]*9;
边界条件:f[1][1]=1;f[1][0]=9;
//【参考程序】
#include
using namespace std;
int main()
{
int f[1001][2],n,i,x;
cin>>n;
f[1][1]=1;f[1][0]=9;
for(i=2;i<=n;i++)
{
x=f[1][0];
if(i==n)x--;
f[i][0]=(f[i-1][0]*x+f[i-1][1])%12345;
f[i][1]=(f[i-1][1]*x+f[i-1][0])%12345;
}
cout<
【例6】过河卒(Noip2002)
【问题描述】
棋盘上A点有一个过河卒,需要走到目标B点。卒行走的规则:可以向下、或者向右。同时在棋盘上的任一点有一个对方的马(如C点),该马所在的点和所有跳跃一步可达的点称为对方马的控制点,如图3-1中的C点和P1,……,P8,卒不能通过对方马的控制点。棋盘用坐标表示,A点(0,0)、B点(n, m) (n,m为不超过20的整数),同样马的位置坐标是需要给出的,C≠A且C≠B。现在要求你计算出卒从A点能够到达B点的路径的条数。

【算法分析】
跳马是一道老得不能再老的题目,我想每位编程初学者都学过,可能是在学回溯或搜索等算法的时候,很多书上也有类似的题目,一些比赛中也出现过这一问题的变形(如NOIP1997初中组的第三题)。有些同学一看到这条题目就去搜索,即使你编程调试全通过了,运行时你也会发现:当n,m=15就会超时。
其实,本题稍加分析就能发现,要到达棋盘上的一个点,只能从左边过来(我们称之为左点)或是从上面过来(我们称之为上点),所以根据加法原理,到达某一点的路径数目,就等于到达其相邻的上点和左点的路径数目之和,因此我们可以使用逐列(或逐行)递推的方法来求出从起点到终点的路径数目。障碍点(马的控制点)也完全适用,只要将到达该点的路径数目设置为0即可。
用F[i][j]表示到达点(i,j)的路径数目,g[i][j]表示点(i, j)有无障碍,g[i][j]=0表示无障碍,g[i][j]=1表示有障碍。
则,递推关系式如下:
F[i][j] = F[i-1][j] + F[i][j-1] //i>0且j>0且g[i][j]= 0
递推边界有4个:
F[i][j] = 0 //g[i][j] = 1
F[i][0] = F[i-1][0] //i > 0且g[i][j] = 0
F[0][j] = F[0][j-1] //j > 0且g[i][j] = 0
F[0][0] = 1
考虑到最大情况下:n=20,m=20,路径条数可能会超过2^31-1,所以要用高精度。
【例7】邮票问题
【问题描述】
设有已知面额的邮票m种,每种有n张,用总数不超过n张的邮票,能从面额1开始,最多连续组成多少面额。(1≤m≤100,1≤n≤100,1≤邮票面额≤255)
【输入格式】
第一行:m,n的值,中间用一空格隔开。
第二行:A[1…m](面额),每个数中间用一空格隔开。
【输出格式】
连续面额数的最大值
【输入样例】stamp.in
3 4
1 2 4
【输出样例】stamp.out
14
【算法分析】
一看到这个题目,给人的第一感觉是用回溯算法,从面额1开始,每种面额都用回溯进行判断,算法复杂度并不高,但是当m,n取到极限值100时,程序明显超时,因此,回溯算法在这里并不可取。 能否用递推完成呢?我们有一个思路:从面额1开始,建立递推关系方程,就用范例来说吧,面额1,2,4只用1张邮票行了,面额3可以表示为面额1,2的邮票和1+1=2,面额5有两种表示方式min(面额1+面额4,面额2+面额3),照此类推,递推关系方程不难建立,就拿邮票问题来说,以下是递推的一种方法:
int n,m,i,j,k;
int c[256]; //面额
int a[31001]; //递推数组
bool b1;
void readfile () { //读入数据
cin >> m >> n;
b1 = true;
for (i = 1; i <= m; i++) {
cin >> c[i];
if (c[i] == 1) b1 = false;
}
}
void work() {
if (b1 == true) cout << "MAX=0"; //不存在面额1时输出无解
else {
i = 1; a[i] = 1;
do {
i++;
for (j = 1; j <= m; j++)
if (((i % c[j] == 0) && ((i / c[j]) < a[i])) || (a[i] == 0))
a[i] = i / c[j]; //判断它能否被题目给定面额整除
for (j = 1; j <= i/2; j++)
if (a[j] + a[i-j] < a[i])
a[i] = a[j] + a[i-j]; //寻找(1<=j<=i),使a[j]+a[i-j]值最小
} while ((a[i] <= n) && (a[i] != 0));
cout << i-1; //输出
}
}
int main ( )
{
readfile() ;
work();
return 0;
}
这种递推方法虽然简单,由于1<=邮票面额<=255,1<=n<=100,因此MAX值最多可达到25500,25500次循环里必定还有嵌套循环,因此算法不加优化,很难在规定时间内得出最优值。这就需要递推的算法优化。 一味递推不寻求算法优化,速度较之搜索提高不少,但一旦数据规模过大,很难在规定时间内得出最优值。 这种递推方法原理是:对于某种要求得到的面额,判断它能否被题目给定面额整除,再寻找(1<=j<=i),使A[j]+A[i-j]值最小,求出凑成某种面额最少邮票数,算法虽然简单,但还可以进一步优化。何不将用m种面额邮票作循环,建立递推关系式:A[i]=MAX(A[I-C[j]]+1),于是当取到极限值时,程序减少了约1.6*10^8次循环,递推优化作用不言而喻。
下面是改进后的程序:
#include
using namespace std;
int x[256];
int pieces[30001];
int m,n,i,j;
int main(){
cin >> m >> n;
for (i = 1; i <= m; i++)
cin >> x[i];
memset(pieces,0,sizeof(pieces));
int maxx = 0;
do //递推循环
{
maxx++;
for (i = 1; i <= m; i++)
if (maxx - x[i] >= 0)
{ //循环,建立递推关系式PIECES[i]=MAX(PIECES[I-X[j]]+1)
if (pieces[maxx] == 0) pieces[maxx] = pieces[maxx-x[i]] + 1;
if (pieces[maxx]>pieces[maxx-x[i]]+1) pieces[maxx] = pieces[maxx-x[i]]+1;
}
if ((pieces[maxx] == 0) || (pieces[maxx] > n))
{
cout << maxx - 1;
break;
}
} while (true);
return 0;
}
五种典型的递推关系
Ⅰ.Fibonacci数列
在所有的递推关系中,Fibonacci数列应该是最为大家所熟悉的。在最基础的程序设计语言Logo语言中,就有很多这类的题目。而在较为复杂的Basic、Pascal、C语言中,Fibonacci数列类的题目因为解法相对容易一些,逐渐退出了竞赛的舞台。可是这不等于说Fibonacci数列没有研究价值,恰恰相反,一些此类的题目还是能给我们一定的启发的。
Fibonacci数列的代表问题是由意大利著名数学家Fibonacci于1202年提出的“兔子繁殖问题”(又称“Fibonacci问题”)。
问题的提出:有雌雄一对兔子,假定过两个月便可繁殖雌雄各一的一对小兔子。问过n个月后共有多少对兔子?
解:设满x个月共有兔子Fx对,其中当月新生的兔子数目为Nx对。第x-1个月留下的兔子数目设为Fx-1对。则:
Fx=Nx+ Fx-1
Nx=Fx-2 (即第x-2个月的所有兔子到第x个月都有繁殖能力了)
∴ Fx=Fx-1+Fx-2 边界条件:F0=0,F1=1
由上面的递推关系可依次得到
F2=F1+F0=1,F3=F2+F1=2,F4=F3+F2=3,F5=F4+F3=5,……。
Fabonacci数列常出现在比较简单的组合计数问题中,例如以前的竞赛中出现的“骨牌覆盖”问题。在优选法中,Fibonacci数列的用处也得到了较好的体现。
Ⅱ.Hanoi塔问题
问题的提出:Hanoi塔由n个大小不同的圆盘和三根木柱a,b,c组成。开始时,这n个圆盘由大到小依次套在a柱上,如图所示。
要求把a柱上n个圆盘按下述规则移到c柱上:

(1)一次只能移一个圆盘;
(2)圆盘只能在三个柱上存放;
(3)在移动过程中,不允许大盘压小盘。
问将这n个盘子从a柱移动到c柱上,总计需要移动多少个盘次?
解:设hn为n个盘子从a柱移到c柱所需移动的盘次。显然,当n=1时,只需把a 柱上的盘子直接移动到c柱就可以了,故h1=1。当n=2时,先将a柱上面的小盘子移动到b柱上去;然后将大盘子从a柱移到c 柱;最后,将b柱上的小盘子移到c柱上,共记3个盘次,故h2=3。以此类推,当a柱上有n(n2)个盘子时,总是先借助c柱把上面的n-1个盘子移动到b柱上,然后把a柱最下面的盘子移动到c柱上;再借助a柱把b柱上的n-1个盘子移动到c柱上;总共移动hn-1+1+hn-1个盘次。
∴hn=2hn-1+1 边界条件:h1=1
Ⅲ.平面分割问题
问题的提出:设有n条封闭曲线画在平面上,而任何两条封闭曲线恰好相交于两点,且任何三条封闭曲线不相交于同一点,问这些封闭曲线把平面分割成的区域个数。
解:设an为n条封闭曲线把平面分割成的区域个数。 由图3-13可以看出:a2-a1=2;a3-a2=4;a4-a3=6。
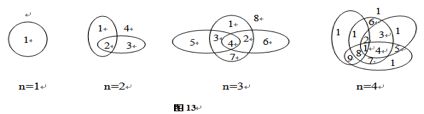
从这些式子中可以看出an-an-1=2(n-1)。当然,上面的式子只是我们通过观察4幅图后得出的结论,它的正确性尚不能保证。下面不妨让我们来试着证明一下。当平面上已有n-1条曲线将平面分割成an-1 个区域后,第n-1条曲线每与曲线相交一次,就会增加一个区域,因为平面上已有了n-1条封闭曲线,且第n条曲线与已有的每一条闭曲线恰好相交于两点,且不会与任两条曲线交于同一点,故平面上一共增加2(n-1)个区域,加上已有的an-1个区域,一共有an-1+2(n-1)个区域。所以本题的递推关系是an=an-1+2(n-1),边界条件是a1=1。
平面分割问题是竞赛中经常触及到的一类问题,由于其灵活多变,常常感到棘手,下面的【例7】是另一种平面分割问题,有兴趣的读者不妨自己先试着求一下其中的递推关系。
Ⅳ.Catalan数
Catalan数首先是由Euler在精确计算对凸n边形的不同的对角三角形剖分的个数问题时得到的,它经常出现在组合计数问题中。
问题的提出:在一个凸n边形中,通过不相交于n边形内部的对角线,把n边形拆分成若干三角形,不同的拆分数目用hn表示,hn即为Catalan数。例如五边形有如下五种拆分方案(图3-14),故h5=5。求对于一个任意的凸n边形相应的hn。 

Catalan数是比较复杂的递推关系,尤其在竞赛的时候,选手很难在较短的时间里建立起正确的递推关系。当然,Catalan数类的问题也可以用搜索的方法来完成,但是,搜索的方法与利用递推关系的方法比较起来,不仅效率低,编程复杂度也陡然提高。
Ⅴ.第二类Stirling数
在五类典型的递推关系中,第二类Stirling是最不为大家所熟悉的。也正因为如此,我们有必要先解释一下什么是第二类Strling数。
【定义2】n个有区别的球放到m个相同的盒子中,要求无一空盒,其不同的方案数用S(n,m)表示,称为第二类Stirling数。
下面就让我们根据定义来推导带两个参数的递推关系——第二类Stirling数。
解:设有n个不同的球,分别用b1,b2,……bn表示。从中取出一个球bn,bn的放法有以下两种:
①bn独自占一个盒子;那么剩下的球只能放在m-1个盒子中,方案数为S2(n-1,m-1);
②bn与别的球共占一个盒子;那么可以事先将b1,b2,……bn-1这n-1个球放入m个盒子中,然后再将球bn可以放入其中一个盒子中,方案数为mS2(n-1,m)。
综合以上两种情况,可以得出第二类Stirling数定理:
【定理】S2(n,m)=mS2(n-1,m)+S2(n-1,m-1) (n>1,m1)
边界条件可以由定义2推导出:
S2(n,0)=0;S2(n,1)=1;S2(n,n)=1;S2(n,k)=0(k>n)。
第二类Stirling数在竞赛中较少出现,但在竞赛中也有一些题目与其类似,甚至更为复杂。读者不妨自己来试着建立其中的递推关系。
小结:通过上面对五种典型的递推关系建立过程的探讨,可知对待递推类的题目,要具体情况具体分析,通过找到某状态与其前面状态的联系,建立相应的递推关系。
练习
1、走楼梯
楼梯有N级台阶,上楼可以一步上一阶,也可以一步上二阶。编一递归程序,计算共有多少种不同走法?
【输入样例】3
【输出样例】3
2、兔子繁殖
有一种兔子,出生后一个月就可以长大,然后再过一个月一对长大的兔子就可以生育一对小兔子且以后每个月都能生育一对。现在,我们有一对刚出生的这种兔子,那么,n个月过后,我们会有多少对兔子呢?假设所有的兔子都不会死亡。
【输入格式】
输入文件仅一行,包含一个自然数n。
【输出格式】
输出文件仅一行,包含一个自然数,即n个月后兔子的对数。
【输入样例】5
【输出样例】5
3、平面分割
同一平面内有n(n≤500)条直线,已知其中p(p≥2)条直线相交于同一点,则这n条直线最多能将平面分割成多少个不同的区域?
【输入格式】两个整数n(n≤500)和p(2≤p≤n)。
【输出格式】一个正整数,代表最多分割成的区域数目。
【输入样例】12 5
【输出样例】73
4、骨牌铺法
有1×n的一个长方形,用一个1×1、1×2和1×3的骨牌铺满方格。例如当n=3时为1×3的方格。此时用1×1、1×2和1×3的骨牌铺满方格,共有四种铺法。如下图:

【输入样例】 3
【输出样例】 4
5、蜜蜂路线
【问题描述】
一只蜜蜂在下图所示的数字蜂房上爬动,已知它只能从标号小的蜂房爬到标号大的相邻蜂房,现在问你:蜜蜂从蜂房M开始爬到蜂房N,M
【输入格式】 输入M,N的值。
【输出格式】 爬行有多少种路线。
【输入样例】 1 14
【输出样例】 377
6、极值问题
【问题描述】
已知m、n为整数,且满足下列两个条件:
① m、n∈{1,2,…,k},即1≤m,n≤k
②(n^ 2-m*n-m^ 2)^2=1
你的任务是:编程输入正整数k(1≤k≤10^9),求一组满足上述两个条件的m、n,并且使m ^ 2+n ^2的值最大。例如,从键盘输入k=1995,则输出:m=987 n=1597。
【输入样例】1995
【输出样例】
m=987
n=1597
7.火车站(Noip1998)
【问题描述】
火车从始发站(称为第1站)开出,在始发站上车的人数为a,然后到达第2站,在第2站有人上、下车,但上、下车的人数相同,因此在第2站开出时(即在到达第3站之前)车上的人数保持为a人。从第3站起(包括第3站)上、下车的人数有一定规律:上车的人数都是前两站上车人数之和,而下车人数等于上一站上车人数,一直到终点站的前一站(第n-1站),都满足此规律。现给出的条件是:共有N个车站,始发站上车的人数为a,最后一站下车的人数是m(全部下车)。试问从x站开出时车上的人数是多少?若无解输出“No answer.”。(所有数据均在长整型数据范围内)
【输入格式】
输入包含一行, 有四个正整数:a(a<=100),n(n<=20),m(m<=10000)和x(x<=19)
【输出格式】
输出为一个整数,为x站开出时车上的人数。
【输入样例】
1 6 7 3
【输出样例】
2
8、数塔问题
【问题描述】 设有一个三角形的数塔,顶点为根结点,每个结点有一个整数值。从顶点出发,可以向左走或向右走,如图所示:
若要求从根结点开始,请找出一条路径,使路径之和最大,只要输出路径的和。

【输入格式】
第一行为n(n<10),表示数塔的层数
从第2行至n+1行,每行有若干个数据,表示数塔中的数值。
【输出格式】输出路径和最大的路径值。
【输入样例】
5
13
11 8
12 7 26
6 14 15 8
12 7 13 24 11
【输出样例】86
9、过河卒(NOIP2002)
【问题描述】
棋盘上A点有一个过河卒,需要走到目标B点。卒行走的规则:可以向下、或者向右。同时在棋盘上的任一点有一个对方的马(如C点),该马所在的点和所有跳跃一步可达的点称为对方马的控制点(如图中的C点和P1,P2,……,P8)。卒不能通过对方马的控制点。棋盘用坐标表示,A点(0,0)、B点(n, m) (n,m为不超过20的整数),同样马的位置坐标是需要给出的,C≠A且C≠B。现在输入B点坐标和C点的坐标,要你计算出卒从A点能够到达B点的路径的条数。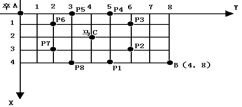
【输入样例】4 8 2 4
【输出样例】0