C语言 最短路径之Dijkstra算法 无向图
-
-
- Dijkstra算法简介
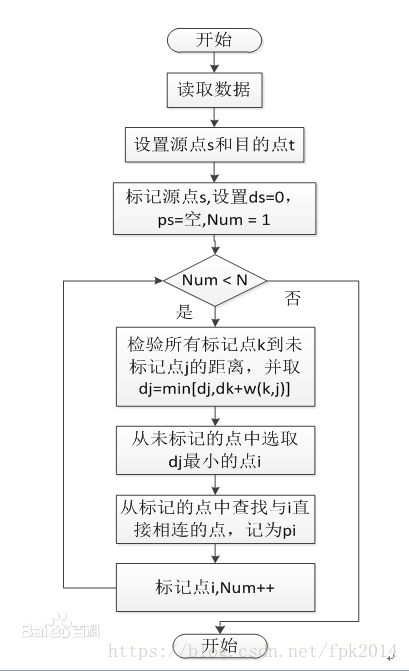
- 实现过程
- 代码实现
- Dijkstra算法简介
-
Dijkstra算法简介
实现过程
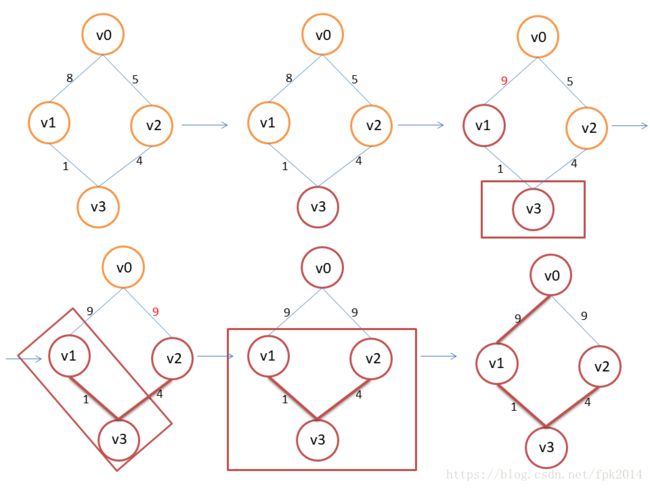
Dijkstra算法和Prim算法非常相似(参照链接:C语言 Prim算法和Kruskal算法的实现和证明)
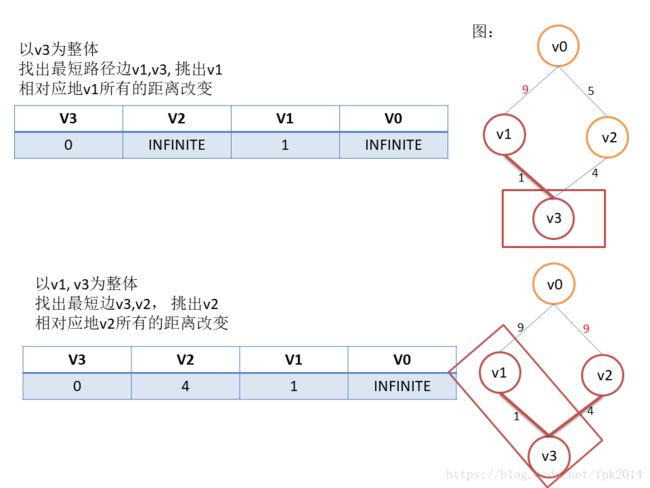
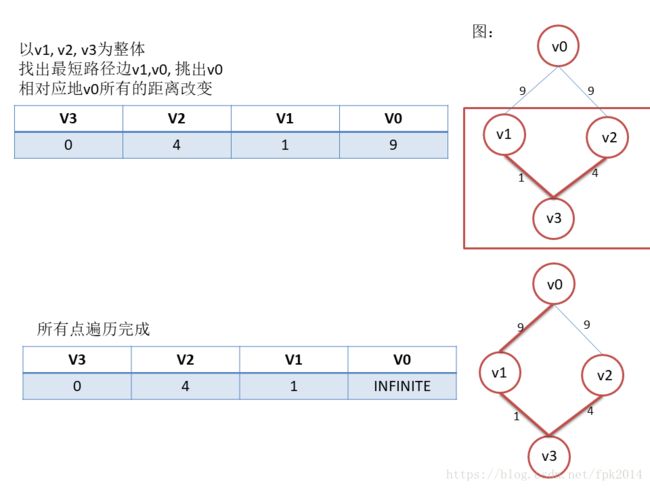
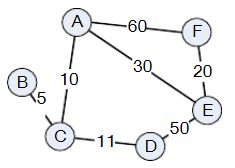
从上面可以看出,Dijkstra算法只是比Prim算法多增加了一个在之后重新计算距离的步骤而已。总的过程:
代码实现
核心代码:
void changeWeight(AdjGraphPtr adj, int *distTo, int pos) {
EdgePtr tmp = adj->vertexList[pos]->firstEdge;
while (tmp != NULL) {
VTYPE to = getVertexPos(adj, tmp->w);
if (distTo[to] != INFINITE) {
tmp = tmp->next;
continue;
}
tmp->weight = tmp->weight + distTo[pos];
tmp = tmp->next;
}
}
void insertEdgeToQueue(AdjGraphPtr spt, QueuePtr minPQ, EdgePtr edge) {
VTYPE a = edge->v;
VTYPE b = edge->w;
int weight = edge->weight;
int pos_a = getVertexPos(spt, a);
EdgePtr tmp = spt->vertexList[pos_a]->firstEdge;
while (tmp != NULL) {
if (edge->v == tmp->v && edge->w == tmp->w) {
return;
}
if (edge->w == tmp->v && edge->v == tmp->w) {
return;
}
tmp = tmp->next;
}
insertQueue(minPQ, edge, 1);
}
BOOLEAN isMarkedAll(int *distTo, int length) {
for (int i = 0; i < length; i++) {
if (distTo[i] == INFINITE) {
return FALSE;
}
}
return TRUE;
}
void dijkstraSPT(AdjGraphPtr adj) {
/**********初始化********/
QueuePtr minPQ = createQueue(); //保存横截边
AdjGraphPtr spt = (AdjGraphPtr)malloc(sizeof(AdjGraph)); //保存路径
memset(spt, 0, sizeof(AdjGraph));
for (int i = 0; i < adj->vNum; i++) {
insertVertex(spt, adj->vertexList[i]->v);
}
spt->vNum = adj->vNum;
int distTo[6]; //保存距离,标记顶点
for (int i = 0; i < 6; i++) {
distTo[i] = INFINITE;
}
/**********初始化********/
EdgePtr tmp = adj->vertexList[0]->firstEdge;
while(tmp != NULL) {
insertQueue(minPQ, tmp, 1);
tmp = tmp->next;
}
distTo[0] = 0;
while (isQueueEmpty(minPQ) == FALSE && isMarkedAll(distTo, 6)==FALSE) {
EdgePtr minEdge = outQueue(minPQ);
VTYPE from = minEdge->v;
VTYPE to = minEdge->w;
int weight = minEdge->weight;
int toPos = getVertexPos(adj, to);
distTo[toPos] = weight;
insertEdge(spt, from, to, weight);
insertEdge(spt, to, from, weight);
changeWeight(adj, distTo, toPos);
EdgePtr tmp = adj->vertexList[toPos]->firstEdge;
while (tmp != NULL) {
insertEdgeToQueue(spt, minPQ, tmp);
tmp = tmp->next;
}
}
deleteQueue(minPQ);
freeAdj(spt);
}
#include