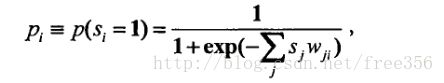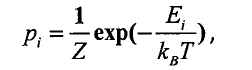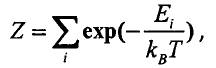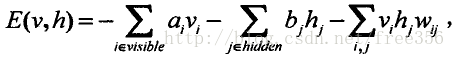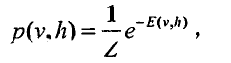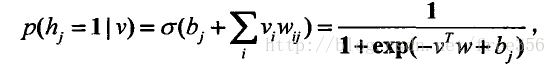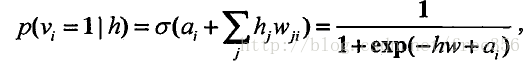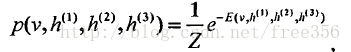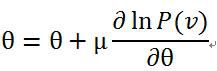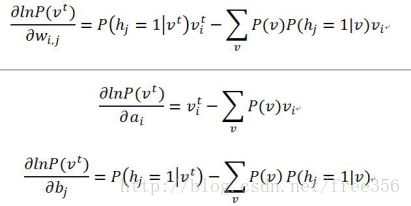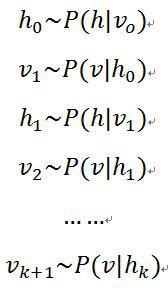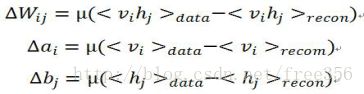基于深度学习的推荐系统研究

基于深度学习的推荐系统研究

论文信息：北京邮电大学   陈达  14年硕毕论

目的：深度网络学习算法应用到推荐系统 。

为此工作：

1）研究分析基于内容的推荐系统和基于协同过滤的推荐系统，包括基于相似度的最近邻方法，朴素贝叶斯方法，潜在因素的矩阵分解方法，分析了各自的优缺点。

2）研究一个典型的深度网络模型——多层受限波兹曼机（DBN）。

3）将深度网络与传统协同过滤方法相结合，建立一个新的深度网络混合模型，采用有限步吉布斯采样的最小化散度差算法对深度模型的似然函数求解，可以训练一个深度网络系统。

4）在多个数据集上，将此方法和传统方法进行对比，证明深度网络学习方法在特征提取上具有不错能力，用在推荐系统上比协同过滤方法有更好的抗噪性和有效性。 

内容一（传统算法优缺点） ：

1，基于内容的推荐算法：TF-IDF，朴素贝叶斯。

2，基于协同过滤的推荐算法：根据相似用户的最近邻，潜在因素的矩阵分解。

内容二（深度网络结构）：

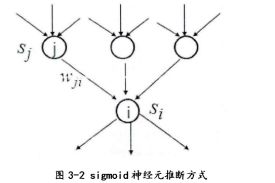
背景知识1：神经网络的神经元，sigmoid神经元

              

                                    

对于一个单层的推断结构利用梯度下降的方式学习权值：

         

上述公式中，字母依次分别代表学习速率，0,1二值，推断的概率。

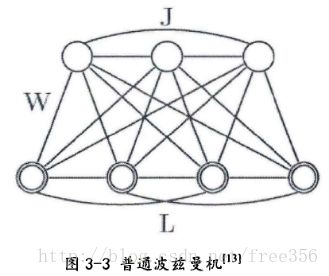
背景知识2：波兹曼机

波兹曼机是由随机神经元函数（sigmoid）组成的随机机器，每个节点的状态只能是“开”和“关”两种状态，用0和1来表示，这里的0和1状态的意义是代表了模型会选取哪些节点来使用，处于激活状态的节点被使用，未处于激活状态的节点未被使用。节点的激活概率由可见层和隐藏层节点的分布函数计算。其神经元分成两部分功能组一一下面一层的可见层神经元和上面一层的隐含层祌经元。在网络的训练阶段所有的可见神经元都被钳制在环境所决定的特定状态，而隐藏神经元总是自由运行的。

 

背景知识3：波兹曼机统计力学与吉布斯分布

有许多自由度的物理系统，它可以驻留在大量可能状态中的任何一个。P表示状态概率，E表示状态的能量（P和E一一对应），当系统和周围环境处于热平衡状态时一个基本的状态的发生概率为：

 

其中T为幵尔文绝对摄氏度，K为波兹曼常数，再根据概率之和为1可以得到在某个状态E下联合概率分布函数：

 

上述分布即符合吉布斯分布。吉布斯分布一个重要的性质：能量低的状态比能量高的状态发生概率较高。

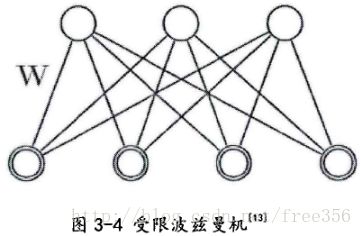
背景知识4：受限波兹曼机

普通波兹曼机简化成了受限波兹曼机，受限波兹曼机隐含层与隐含层之间无连接，可见层与可见层之间无连接，如下：

 

在可见层和隐含层加入了偏好之后的受限波兹曼机的联合能量函数为：

 

其中i,j分别为可见层和隐含层神经元的个数，a可见层偏好，b为隐含层偏好，w为可见层和隐含层的连接权值。而可见层单元根据不同的应用情景有不同的取值范围和不同的神经元函数。

整个网络在状态X下的概率用能量函数表示：

 

这里注意v和h为可见层向量和隐含层状态向量，状态X下的联合概率分布为：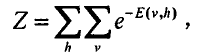

 

由于隐含层与隐含层之间无连接，可见层与可见层之间无连接，更重要的性质是：当给定了可见层的数据之后隐含层之间是条件独立的，给定了隐含层的数据之后可见层之间是条件独立的。

当给定可见层状态时，隐含层的某一个单元处于“激活”态概率为：

 

当给定隐含层状态时，可见层某一单元处于“激活”态概率为：

 

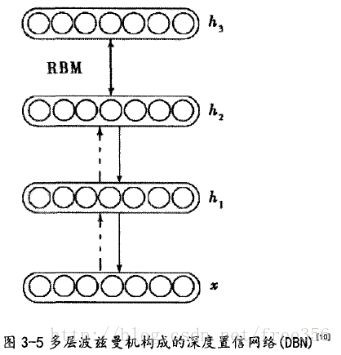
背景知识5：多层波兹曼机

 

该图的最下层为可见层V，可见层之上的均为隐含层H，在多层情况下以三层为例，整个网络的联合能量函数为：

 

网络在状态X下的联合概率：

 

在深度置信网络中利用最顶两个隐含层作为无向的关键记忆层(如图的双向箭头），将关联记忆表征的信息可以通过网络的重构反应到整个网络的参数上去，这样就可以进行“重复”学习的过程。

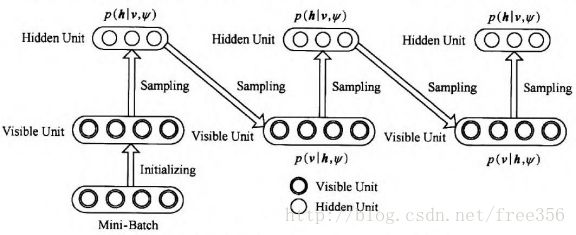
令J表示可见层的输入数据，通常来说波兹曼机的运行状态分为两个阶段：

1，正向推断，这时整个网络在钳制环境下即在输入数据的直接影响下运行；

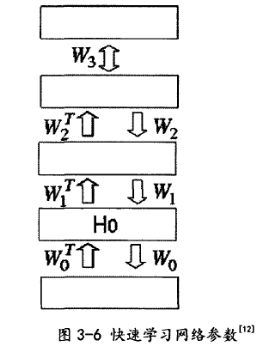
2，负向阶段，这个阶段中网络自由运行，隐含层不断自行推断进行状态转移，并且没有环境输入。那么深度结构波兹曼机的整个网络快速学习权值过程大致如图所示：

 

上图显示了一个快速的学习过程，向上的箭头表示利用该层钳制的数据和权值正向推断的过程，向下的箭头表示作为生成模型，模型重构出来的数据，而且网络的参数是一层一层地向上学习，也就是说当底层参数学习完毕后，将底层向上正向推断的数据作为可见层数据，再向上正向推断学习。

理解参考：https://www.cnblogs.com/jhding/p/5687696.html

内容三（深度结构模型的推荐算法）：

一：深度模型

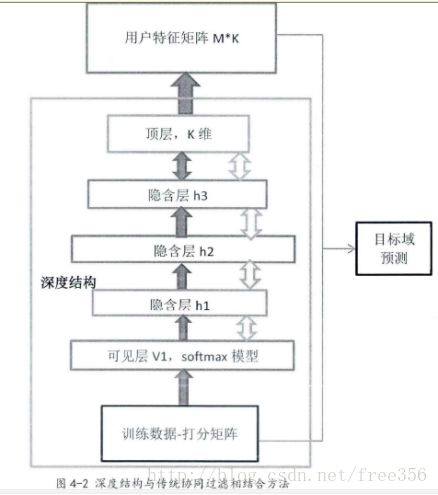
将深度波兹曼机的模型和传统最近邻的方法相结合，利用深度波兹曼机对高维数据的特征抽象表达能力和最近邻直观的而快速的打分预测能力，组成一个新的模型，对己存在的方法进行改进和提升，使其能够充分利用两个模型中出色特点避免两者中的缺点，扬长避短。

 

绿色框部分代表深度学习结构，用模型对训练数据进行输入，并利用无监督学习的方法训练深度网络，该深度模型一共有四层，包括可见层v1，隐含层h1、隐含层h2和隐含层h3，而顶层与隐含层h3形成无向的关联记忆层。

当数据通过深度结构进行深层映射后，从原来的M维（M为输入数据的维度）变成了最顶层的K维数(K为深度模型最顶层神经元的维度），这样我们认为原来高维数据通过特征探测群进行映射后，将数据内部隐含的特征映射到K维空间中。

比如，对于电影打分数据，我们将映射后的K维空间可以理解成该用户对M部电影的偏好特征，1-K个维度分别代表用户喜爱某个演员的程度、喜欢某个类型影片的程度、喜欢某个导员的程度等等，在这K个维度上我们对每个用户的数据进行聚类或者相似度比较，则相似度比较的结果往往比用原始数据进行比较的准确度要高。

二：多层模型的训练方法

要确定这个模型要知道模型的三个参数，下面就围绕着参数的求解进行分析。

参数求解用到了似然函数的对数对参数求导。由于从可知，能量E和概率P是成反比的关系，所以通过最大化P，才能使能量值E最小。最大化似然函数常用的方法是梯度上升法，梯度上升法是指对参数进行修改按照以下公式：

 

通过求关于的导数，即，然后对原值进行修改。如此迭代使似然函数P最大，从而使能量E最小。

对数似然函数对参数求导分析：

首先是对数似然函数的格式：， 表示模型的输入数据。然后对里的参数分别进行求导，详细的推导过程就不写了：

 

由于上面三式的第二项中都含有， 中仍然含有参数，所以它是式中求不出来的。所以，有很多人就提出了一些通过采样逼近的方法来求每一个式子中的第二项。

求解的算法：

1， Gibbs采样算法

因为在上一章节末尾讲对参数的求导中仍然存在不可求项，表示可见层节点的联合概率。所以，要想得到 的值，就得要逼近它，求它的近似值。

Gibbs采样的思想是虽然不知道一个样本数据的联合概率P(x)，但是知道样本中每一个数据的条件概率 （假设每一个变量都服从一种概率分布），则我可以先求出每一个数据的条件概率值，得到x的任一状态 。然后，我用条件概率公式迭代对每一个数据求条件概率。最终，迭代k次的时候，x的某一状态将收敛于x的联合概率分布P(x)。

对于RBM来讲，则执行过程如图3所示：

                

图3 Gibbs采样过程

求解过程是：假设给我一个训练样本v0，根据公式 求 h0中每个节点的条件概率，再根据公式 求v1 中每个节点的条件概率，然后依次迭代，直到执行K步（K足够大），此时的概率将收敛于P(v)的概率。如下所示：

                           

 2，CD-k算法

CD算法是需要k次（k=1）Gibbs采样对可见层节点进行重构得到可见层节点的概率分布。其思想是：假设给模型一个样本v0，通过求所有隐藏层节点的概率值，然后每一个概率值和随机数进行比较得到每一个隐藏层节点的状态，然后通过公式求每一个可见层节点的概率值，再由求每一个隐藏层节点的概率值。最后参数梯度的计算公式变为：

 

其中，μ是学习率，data和recon分别表示训练数据的概率分布和重构后的概率分布。

通过以上方法都可以求出参数的梯度来，由每一个参数的梯度对原参数值进行修改来使模型的能量减小。

内容四（MovieLens数据集实验）：

Movielens数据集：943个用户，1682部电影，100000条评分。

该数据有四列，第一列为评价序号，序号数最大为1000000，第二列代表用户的ID，第三列代表项目的ID，第四列代表用户对该项目的评价，通常来说，评价一般分为1到5五个等级，用户对物品的喜爱程度由小到大。

1，数据预处理

在该数据中按照百分比抽样，形成训练数据和测试数据。将数据形成一个943*1682的矩阵形式。

2，算法设计与实践

对于每一个用户的数据，分别建模，输入到模型中迭代调整权值，于是对于任意一个输入，我们需要将用户的打分数据形成softmax结构的输入，这里我们采用一个三维矩阵uatrainF(k,uraw,col)来记录softmax模型，其中K代表该列中的第K个softmax，uraw和col分别代表原始矩阵的行和列，当数据进入模型时将uatrainF(k,uraw,col)的第二维(用户)抽取出来，输入模型算法，如下：

 

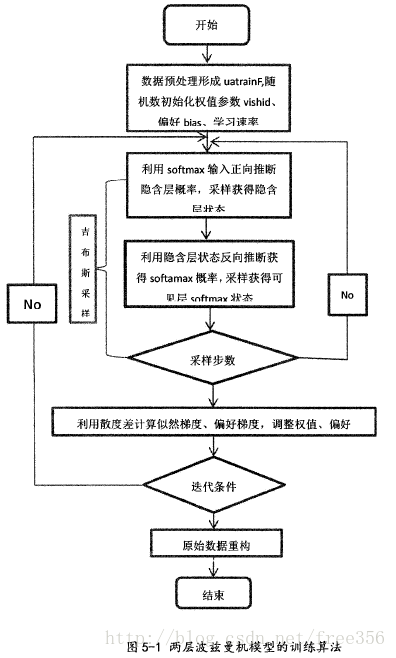
上图表示了一个可见层为softmax的两层波兹曼机模型的训练算法流程图，在初始化阶段，我们需要对模型的众多参数进行初始化，这些参数包括：权值学习速率、可见层偏好学习速率、隐含层偏好、权值代价因子、权值记忆因子、以及连接权值参数、可见层偏好、隐含层偏好，这些随机初始化的方法通常利用均匀分布随机数，或者标准正态分布随机数。进入迭代之后，进行正向推断和反向推断。

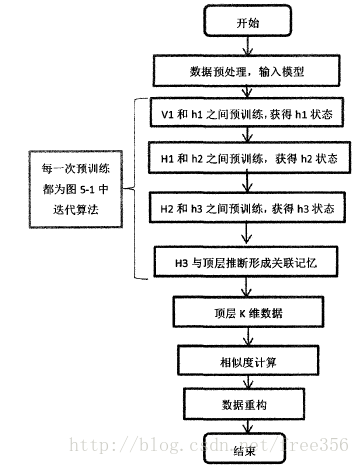
对深度模型的建模工作，可利用上述两层波兹曼机的建模方法，只是除了在第一层和第二层网络上与上述方法相同，第二层到顶层，隐含层神经元釆用的都是普通的{0,1}二值的神经元。将上图的过程称为两层之间的预训练，那么深度结构在相邻的两层之间都会有预训练的过程，由于我们的训练数据并没有标签数据，于是该模型不同于DBN—样存在着微调反馈这一阶段。模型算法流程图如图所示：

 

在预学习阶段，下一层隐含层的输出均作为上一层隐含层的输入。，将原来高维数据通过无监督学习在低维度重新表征出来。其中该网络的H1，H2，H3的维度分别为1000,500，250,V1的维度即为输入矩阵的列数1628，关于每一层神经元的个数的确定可参考上述链接指出，深层网络的中间层神经元较多时效果较好。接下来，对该低维数据重新进行相似度计算利用基于相似度计算的方法进行数据重构。

3，实验结果评价方法

采用均方根误差（RMSE）来衡量真实评分数据和预测的评分数据的差距。

 

 

内容五（论文改进）：

1，MATLAB上运行，内存不够。

2，在Hadoop平台上的并行化。