Tensorflow学习笔记: tf.nn.conv2d函数与tf.nn.depthwise_conv2d函数

参数

首先需要注意的是, tf.nn.conv2d与tf.nn.depthwise_conv2d两个函数的参数基本相同, 具体如下所示
$\text{input}$: 指该卷积层的输入, 通常为图像. 输入的维数为由参数$\text{data\_format}$决定, 具体见该参数说明.
$\text{filter}$： 相当于CNN中的卷积核，要求是一个4维Tensor，四个维数大小依次为卷积核高度, 卷积核宽度, 输入通道数量以及输出通道数量(在depthwise_conv2d中为输出通道乘子), 记为$\mathbf{W}\in {\mathbb{R}}^{H_f\times W_f\times C_i\times C_o(C_m)}$.
$\text{strides}$： 卷积的滑动步长, 通常为长度为4的向量, 表示卷积核在4个维度上的滑动步长, 记为$\mathbf{s}={\left[s_N,s_H,s_W,s_C\right]}^T$.
$\text{padding}$： string类型的量, 只能是”SAME”或”VALID”其中之一, 这个值决定了不同边缘填充方式.
$\text{data\_format}$: string类型的变量, 用于指定输入数据的shape, 取值为"NHWC"与"NCHW"中的一个. 其中, $N$表示批大小(batch size), $H$表示高度(height), $W$表示宽度(width), $C$表示输入通道(channel). 默认值通常为"NHWC", 此时记输入数据为$\mathbf{I}\in {\mathbb{R}}^{N\times H_i\times W_i\times C_i}$

计算过程

在计算过程中, 两个函数的计算方式仅在卷积后求和时有所区别. 因此, 这里介绍一下卷积的计算过程.

卷积计算

对于输入$\mathbf{I}\in {\mathbb{R}}^{N\times H_i\times W_i\times C_i}$与卷积核$\mathbf{W}\in {\mathbb{R}}^{H_f\times W_f\times C_i\times C_o}$, 卷积操作表示为
$$\mathbf{O}=\mathbf{I}\ast \mathbf{W}$$
根据输入的参数, 卷积操作的具体计算方法可分为"VALID"与"SAME"两种, 我们使用一维卷积来介绍这两种计算过程的区别, 首先定义输入$\mathbf{I}$ 的长度(Length)为$L_i$, 即$\mathbf{I}\in {\mathbb{R}}^{L_i}$, 卷积核为$\mathbf{W}\in {\mathbb{R}}^{L_f}$, 滑动步长为$s_L$.

首先需要注意的是, "VALID"与"SAME"本质上的区别在于输出的大小与输入大小是否相同(即SAME表示的是输出大小与输入大小相同), 而控制这一点的方法则是通过在输入两侧(一维情况是两侧, 二维则是上下左右四侧, 亦可扩展至三维输入中)增加0, 具体过程将在padding = "SAME"的章节中进行分析. 接下来首先介绍padding = "VALID"的情况.

padding = “VALID”

VALID情况的下卷积过程如图所示

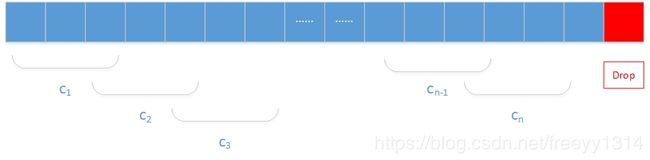
卷积过程从第一个元素开始, 然后根据滑动步长进行滑动. 需要注意的是, 为了使卷积时卷积核对应位置不会超出输入范围, 有时候需要舍弃最后一些元素, 这是由于在卷积时, 最后一次卷积核对应位置的末位索引不能超过输入长度, 即满足下式
$$(n-1)s_L+1+(L_f-1)\le L_i$$
即可得到卷积操作的次数$n$
$$n=\lfloor \frac{L_i-L_f}{s_L}\rfloor +1$$
其中, $\lfloor \rfloor$表示下取整. 而舍弃(Drop)的长度则为
$$L_d=L_i-\left[(n-1)s_L+L_f\right]$$

padding = “SAME”

SAME情况的卷积过程如图所示
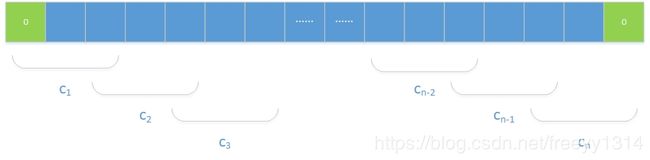可以看到, 在输入的前后分别添加了一些元素使得卷积过程满足一些条件, 称为padding(通常添加的为0元素, 称为zero-padding). 接下来将详细讨论添加元素的规则.

在前面提到过, SAME的意义是使得输出与输入的长度相等. 然而, 这只是当滑动步长为1时的情况. 不过这也为卷积的滑动步长大于1时的操作提供了一个基准原则. 事实上, 在任意滑动长度$s_L$下, 输出长度$L_o$满足下式
$$L_o=\lceil \frac{L_i}{s_L}\rceil$$
其中, $\lceil \rceil$表示上取整. 在大部分情况下(特殊情况后面再介绍), 该输出长度使得卷积操作无法在原始输入上进行, 而是需要对输入进行长度上的扩展, 即padding. 扩展的长度为
$$L_p=(L_0-1)s_L+L_f-L_i$$
事实上, 当$\frac{L_i}{s_L}$为整数时, 即$L_o=\lceil \frac{L_i}{s_L}\rceil =\frac{L_i}{s_L}$, 有
$$L_p=(L_0-1)s_L+L_f-L_i=L_f-s_L$$
因此, 当且仅当$L_i$可被$s_L$整除, 且$L_f=s_L$, 即滑动步长与卷积核的长度相等时, padding的长度为零.

在得到padding的长度后, 除长度为0的情况外, 可分为奇数与偶数两种情况, 这两种情况下输入左右两侧添加的元素数量规则如下.

1. $L_p$为偶数
   这种情况比较简单, 左右填充相同数量的元素, 即
   $$L_{pl}=L_{pr}=\frac{L_p}{2}$$
2. $L_p$为奇数
   当$L_p$为奇数时, 遵循左奇右偶的原则, 即
   $$\{\begin{array}{l}{L}_{pl}=n_1\\ L_{pr}=n_2\end{array}$$
   其中$n_1$为奇数, $n_2$为偶数且有$n_1+n_2=L_p$

未完待续