TensorFlow 实现神经网络
实现效果网站
步骤:
- 输入数据
- 定义网络结构(向前传播)
- 训练网络中参数取值
- 用训练好的网络预测新的数据
文章目录
- 向前传播算法
- 神经网络参数
- 批量传输
- 一个简单的完整的神经网络模型
- 激活函数
- 神经网络优化算法
- 学习率设置
- 滑动平均模型
- MINIST 数字识别问题
- 读取MINIST手写数据集
向前传播算法
- 输入: x = ( x 1 , x 2 , ⋯ , x n 0 ) x=(x_1,x_2,\cdots,x_{n_0}) x=(x1,x2,⋯,xn0)
- 中间层
- 第一层 a ( 1 ) = ( a 11 , a 12 , ⋯ , a 1 n 1 ) a^{(1)}=(a_{11},a_{12},\cdots,a_{1{n_1}}) a(1)=(a11,a12,⋯,a1n1)
- 第二层 a ( 2 ) = ( a 2 , 1 , a 2 , 2 , ⋯ , a 2 , n 2 ) a^{(2)}=(a_{2,1},a_{2,2},\cdots,a_{2,{n_2}}) a(2)=(a2,1,a2,2,⋯,a2,n2)
- ⋯ \cdots ⋯
- 第 m − 1 m-1 m−1层 a ( m − 1 ) = ( a m − 1 , 1 , a m − 1 , 2 , ⋯ , a m − 1 , n m − 1 ) a^{( m-1)}=(a_{m-1,1},a_{m-1,2},\cdots,a_{m-1,{n_{m-1}}}) a(m−1)=(am−1,1,am−1,2,⋯,am−1,nm−1)
- 输出层: y y y
第一层第一个参数计算:
a 11 = ∑ i = 1 n 1 x i w i , 1 ( 1 ) a_{11}=\sum_{i=1}^{n_1} x_iw^{(1)}_{i,1} a11=i=1∑n1xiwi,1(1)
第一层参数的计算: a ( 1 ) = x W ( 1 ) = ( x 1 , x 2 , ⋯ , x n 0 ) ( w 1 , 1 ( 1 ) w 1 , 2 ( 1 ) ⋯ w 2 , 1 ( 1 ) w 2 , 2 ( 1 ) ⋯ ⋮ ⋮ ⋱ ⋮ w n 0 , 1 ( 1 ) w n 0 , 2 ( 1 ) ⋯ w n 0 , n 1 ( 1 ) ) . a^{(1)}=xW^{(1)}=(x_1,x_2,\cdots,x_{n_0})\begin{pmatrix}w^{(1)}_{1,1} & w^{(1)}_{1,2} && \cdots \\ w^{(1)}_{2,1} & w^{(1)}_{2,2} && \cdots \\ \vdots & \vdots &\ddots & \vdots \\ w^{(1)}_{n_0,1} & w^{(1)}_{n_0,2} & \cdots & w^{(1)}_{n_0,n_1} \end{pmatrix} . a(1)=xW(1)=(x1,x2,⋯,xn0)⎝⎜⎜⎜⎜⎛w1,1(1)w2,1(1)⋮wn0,1(1)w1,2(1)w2,2(1)⋮wn0,2(1)⋱⋯⋯⋯⋮wn0,n1(1)⎠⎟⎟⎟⎟⎞.
第二层参数的计算: a ( 2 ) = a ( 1 ) W ( 2 ) a^{(2)}=a^{(1)}W^{(2)} a(2)=a(1)W(2)
⋯ ⋯ \cdots \cdots ⋯⋯
第 m − 1 m-1 m−1层参数的计算: a ( m − 1 ) = a ( m − 2 ) W ( m − 1 ) a^{(m-1)}=a^{(m-2)}W^{(m-1)} a(m−1)=a(m−2)W(m−1)
输出层: y = a ( m − 1 ) W m = ( a m − 1 , 1 , a m − 1 , 2 , ⋯ , a m − 1 , n m ) ( w 1 , 1 ( m ) w 1 , 2 ( m ) ⋯ w 2 , 1 ( m ) w 2 , 2 ( m ) ⋯ ⋮ ⋮ ⋱ ⋮ w n m − 1 , 1 ( m ) w n m − 1 , 2 ( m ) ⋯ w n m − 1 , n m ( m ) ) . y=a^{(m-1)}W^m=(a_{m-1,1},a_{m-1,2},\cdots,a_{m-1,{n_m}}) \begin{pmatrix}w^{(m)}_{1,1} & w^{(m)}_{1,2} && \cdots \\ w^{(m)}_{2,1} & w^{(m)}_{2,2} && \cdots \\ \vdots & \vdots &\ddots & \vdots \\ w^{(m)}_{n_{m-1},1} & w^{(m)}_{n_{m-1},2} & \cdots & w^{(m)}_{n_{m-1},n_{m}} \end{pmatrix} . y=a(m−1)Wm=(am−1,1,am−1,2,⋯,am−1,nm)⎝⎜⎜⎜⎜⎛w1,1(m)w2,1(m)⋮wnm−1,1(m)w1,2(m)w2,2(m)⋮wnm−1,2(m)⋱⋯⋯⋯⋮wnm−1,nm(m)⎠⎟⎟⎟⎟⎞.
矩阵乘法的代码:
a1=tf.matmul(x,w1)
y=tf.matmul(a(m-1),wm)
神经网络参数
将神经网络参数设置维TensorFlow的变量
weights=tf.Variable(tf.random_normal([2,3],stddev=2))
这里是指申明一个 2 × 3 2 \times 3 2×3的矩阵变量weights,矩阵中的元素均值是0,标准差为2.
我们可以通过这种方式定义所有的参数。然后我们需要定义一个会话来计算 y y y的值。在计算它之前,需要对所有的变量初始化。前面只给了初始化的方法,并没有运行它。所以我们可以通过下面这个函数初始化所有变量
sess=tf.Session()
init_op=tf.global_variables_initializer()
sess.run(init_op)
批量传输
import tensorflow as tf
w1=tf.Variable(tf.random_normal([2,3],stddev=1,seed=1))
w2=tf.Variable(tf.random_normal([3,1],stddev=1,seed=1))
x=tf.placeholder(tf.float32,shape=(3,2),name="input")
a=tf.matmul(x,w1)
y=tf.matmul(a,w2)
sess=tf.Session()
init_op=tf.global_variables_initializer()
sess.run(init_op)
print(sess.run(y,feed_dict={x:[[0.7,0.9],[0.1,0.4],[0.5,0.8]]}))
如果每一轮迭代,数据都要用常量表示,那么tensorflow计算图会非常大。为了避免这种情况发生,这里采用placeholder机制。
placeholder相当于定义了一个位置,数据在运行烦人时候再指定。
上面代码的第6行: x x x用placeholder机制占一个位置
在第 14 14 14行用 feed_dict 来指定 x x x的取值
输出结果为
一个简单的完整的神经网络模型
import tensorflow as tf
from numpy.random import RandomState
batch_size=8
w1=tf.Variable(tf.random_normal([2,3],stddev=1,seed=1))
w2=tf.Variable(tf.random_normal([3,1],stddev=1,seed=1))
x=tf.placeholder(tf.float32,shape=(None,2),name='x-input')
y_=tf.placeholder(tf.float32,shape=(None,1),name='y-input')
a=tf.matmul(x,w1)
y=tf.matmul(a,w2)
y=tf.sigmoid(y)
cross_entropy=-tf.reduce_mean(y_* tf.log(tf.clip_by_value(y,1e-10,1.0))+(1-y_)*tf.log(tf.clip_by_value(1-y,1e-10,1.0)))
train_step=tf.train.AdamOptimizer(0.001).minimize(cross_entropy)
rdm=RandomState(1)
dataset_size=128
X=rdm.rand(dataset_size,2)
Y=[[int(x1+x2<1)] for (x1,x2) in X]
with tf.Session() as sess:
init_op=tf.global_variables_initializer()
sess.run(init_op)
print sess.run(w1)
print sess.run(w2)
STEPS=5000
for i in range(STEPS):
start=(i*batch_size)
end=min(start+batch_size,dataset_size)
sess.run(train_step,feed_dict={x: X[start:end],y_: Y[start:end]})
if i % 1000 ==0:
total_cross_entropy=sess.run(cross_entropy,feed_dict={x:X,y_:Y})
print("After %d training step(s),cross entropy on all data is %g",(i,total_cross_entropy))
print sess.run(w1)
print sess.run(w2)
激活函数
上面的例子都是线性结构,它具有非常大的局限性。下面介绍非线性结构:激活函数. f ( a W + b ) f(aW+b) f(aW+b)其中 f ( ⋅ ) f(\cdot) f(⋅)是激活函数.
例如 ReLU函数: f ( x ) = max ( x , 0 ) f(x)=\max (x,0) f(x)=max(x,0)
a=tf.nn.relu(tf.matmul(x,w1)+biases1)
神经网络优化算法
设损失函数为: J ( θ ) J(\theta) J(θ),其中 θ \theta θ是网络参数.
优化过程寻找一组参数 θ \theta θ使得损失函数 J ( θ ) J(\theta) J(θ)达到最小.迭代公式为:
θ n + 1 = θ n − η ∂ ∂ θ n J ( θ n ) \theta_{n+1}=\theta_n-\eta \frac{\partial}{\partial \theta_n}J(\theta_n) θn+1=θn−η∂θn∂J(θn)
其中 η \eta η为学习率.
梯度下降法并不能保证被优化的函数达到全局最优解,可能只是局部最优解.另一个问题是计算时间太长.
梯度下降法要计算在全部训练数据上最小化损失,所以损失函数 J ( θ ) J(\theta) J(θ)是在所有训练数据上的损失和.这样在每一轮迭代中都需要计算在全部训练数据上的损失函数,在海量训练数据下,非常耗时间.
随机梯度下降法:在每一轮迭代中,随机优化某一条训练数据上的损失函数.优点:速度加快了;缺点: 每次只优化某一条数据上的损失函数,不代表所有数据的全局最优
综上,实际运用中每次计算一小部分训练数据的损失函数。称这一小部分数据为batch
学习率设置
学习率过大不收敛,学习率过小迭代速度太慢.
指数衰减法:先使用较大的学习率快速得到一个比较优的解,而后随着迭代的继续逐步减少学习率,使得模型在训练后期更加稳定.
TensorFlow提供了一个指数函数exponential_decay:指数级减小学习率
decayed_learning_rate=learning_rate * decay_rate ^ (global_step / decay_steps)
- decayed_learning_rate:每一轮优化时使用的学习率
- learning_rate :事先设置的初始学习率
- decay_rate:衰减系数
- decay_steps:衰减速度
滑动平均模型
用于控制模型的更新速度
MINIST 数字识别问题
教程
读取MINIST手写数据集
TensorFlow提供了一个类来处理MNIST数据
首先下载数据集 数据集下载地址
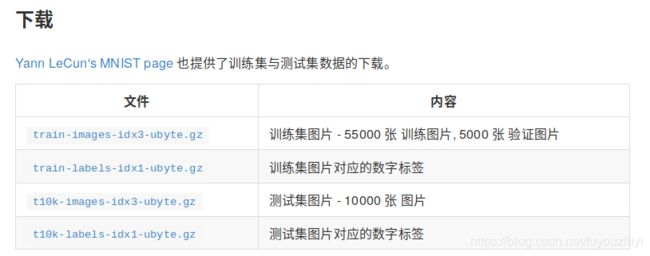
读取文件名为:trymnist.py,放在code文件夹下
数据集放在 code/data文件夹下
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("data/", one_hot=True)
print "Training data size:",mnist.train.num_examples
print "Validating data size:",mnist.validation.num_examples
print "Tseting data size:",mnist.test.num_examples
print "Example training data:",mnist.train.images[0]
print "Example training data label:",mnist.train.labels[0]