数学建模笔记

一、katex公式编辑文档

https://khan.github.io/KaTeX/docs/supported.html

---

二、公式编辑示例

```katex
{% katex [displayMode] %}
a^{b^{\sqrt{c}}}
{% endkatex %}
```

---

三、scipy.optimize

功能清单-查看官方api

• 优化（minimize or optimize）

  • 局部优化 (local ~求局部最小值) --minimize()
  • 全局优化 (global ~)

• 拟合 (fitting)

  • 最小二乘法 --curve_fit()

• 求根(root finding)或不动点(fixed point)

  • 二分法、牛顿法求解,分标量和矢量（即维度）

• 线性规划

  • linprog()
  • 由于scipy不支持整数线性规划问题，推荐使用pulp模块求解线性规划，不过据说lingo是线性规划问题的最优选择

---

四、线性规划问题(linear programming)

• 常规线性规划，目标函数+条件(不等式与等式条件)
• 整数规划、混合整数规划、0-1规划

---

五、Matlab命令

• vpa()转化为小数表达形式
• vpasolve(),roots()求方程实数解（去掉Real参数可求符号通解）,daolve解微分方程

  syms x
  vpasolve(x^4 - 7*x^3 + 3*x^2 - 5*x + 9,x)
  

  等价于

  roots([1 -7 3 -5 9])  % 系数对齐
  

• limit(fun,point)，求函数极限
• diff(fun), 求符号导数
• int(fun，[a,b]), 求符号不定积分或定积分
• subs(fun,value),符号函数求值
• isequal(A,B) 判断两个值是否相等(可以为数组或矩阵，或符号函数)
• fminsearch(fun,x0)，fminunc(fun,x0)求解无约束局部优化问题,后者只能用于求解连续函数，但计算效率较高。
• fmincon(fun,x0,A,b,Aeq,Beq,Lb,Ub)，linprog(...)求解有约束线性优化
• syms()可以同时声明多个变量以及符号函数，sym不能声明符号函数
• ezplot画椭圆曲线（隐函数）：

  syms f(x)
  f(x) = x^2 +3*y^2 -5
  ezplot(f)
  

• plot函数可以话折线图或散点图，当传入的linespace为maker时就是散点图。
• ax = gca,获取当前坐标轴句柄，从而可以设置坐标轴相对位置，刻度，标签等信息。
• minmax()返回一个矩阵中每行的最小值和最大值

---

• newff()新建一个feed-forward backpropagation network（前馈反向传播网络）.
• 要有 fsolve fzero roots solve；其中solve是符号求解，换句话说是精确解；其它都是数值解； fsolve可以求解方程组； fzero只能求解一元方程； roots只能求解多项式； f**每次只能求解一个根，并且需要提供初值，而是roots和solve尽量找出所有的跟。

六、数学建模方法

• 机理分析，通过对实际问题原理进行分析，建立相应的模型，即白箱问题。
• 测试分析，黑箱问题，问题内部原理不可知，通过对观测数值进行拟合。
• 一般结合两种方式解决问题，通过机理分析初步建立模型，测试分析确定参数。

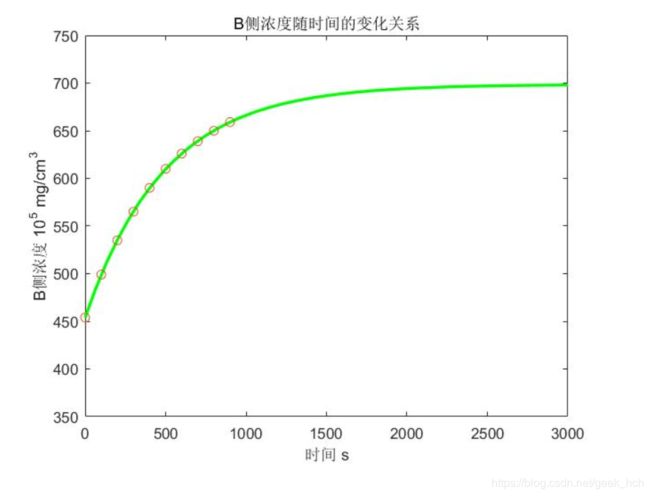
  % 暑期作业第二题
  % 对应数据变为
  T = [0:100:900];
  C = [454 499 535 565 590 610 626 639 650 659];
  V = 1000;
  S = 10;
  % 假设条件：
  % 1. 薄膜两侧表面各处的液体浓度均匀
  % 2. 以100s时为起始时间
  % 3. 总质量为m，C1*V1+C2*V2 = m， 设C1+C2 = m/V = M
  % 4. t时刻，A测浓度为x(t)
  % 设记录的浓度为A侧浓度，该浓度随时间推移而增大。
  syms M x(t) K a p xdata;
  eq = diff(x) == K*(M-2*x);
  x(t) = dsolve(eq,x(0)==454);
  fun1 = matlabFunction(x);
  fun2 = @(p,xdata) fun1(xdata,p(1),p(2));
  p = lsqcurvefit(fun2,[1,1],T,C);
  
  fun2(p,T)
  ans =
  454   597   597   597   597   597   597   597   597   597
  

• 量纲分析：由量纲齐次原则建立等量关系，建立方程组求出各物理量之间的指数关系 《姜起源建模197页》

---

七、最小二乘拟合中的坑（初始参数设置技巧）

• 参数初始值对拟合影响很大，包括能否拟合出结果以及拟合结果的正确性，今天用血的体验证明了拟合可能存在局部陷阱。下面来说说今天遇到的问题。

  % 暑期作业第二题
  T = [0:100:900];
  C = [454 499 535 565 590 610 626 639 650 659];
  V = 1000;
  S = 10;
  % 假设条件：
  % 1. 薄膜两侧表面各处的液体浓度均匀
  % 2. 以100s时为起始时间
  % 3. 总质量为m，C1*V1+C2*V2 = m， 设C1+C2 = m/V = M
  % 4. t时刻，A测浓度为x(t)
  % 设记录的浓度为A侧浓度，该浓度随时间推移而增大。
  syms M x(t) K a p xdata;
  eq = diff(x) == K*(M-2*x);
  x(t) = dsolve(eq,x(0)==454);
  fun1 = matlabFunction(x);
  
  % 用于拟合的目标函数
  fun2 = @(p,xdata) fun1(xdata,p(1),p(2));
  % 拟合
  p = lsqcurvefit(fun2,[1,1],T,C);
  % 检验
  fun2(p,T)
  ans =
  454   597   597   597   597   597   597   597   597   597
  

  上面的检验结果和真实情况相差甚远，画出函数图像
  
  再查看带入参数的函数表达式

  >> fun1
  

$$ans=@(t,K,M)\left(\frac{M}{2}-\frac{e^{-2Kt}\ast (M-908)}{2}\right)$$

• 可以看出，参数p(2),即两侧浓度总和决定函数趋于无穷大的渐近线，根据题意，C值估计在1000左右，而图像之所以像直线，是因为exp的指数太大，导致变化太快，指数部分很快减小为0，为了减缓这种变化，按10倍减小参数p1到0.001,此时拟合出正确的结果。
  $$ans=698.5-244.5\ast e^{-0.002024t}$$
  

当然，这远远没有结束,拟合时返回的雅可比矩阵不知道有什么用呢？

---

八、培训简记

• 机器学习经典算法
• 网络模型
• 非线性模型优化比较困难，即使使用matlab也可能由于没有正确设置初始参数而找不到全局最优解。因此可以使用换元等方法来线性化。如$$I=a{e}^{bv}$$,可以取对数后再换元，从而得到一个线性的目标函数。

• 常微分方程的解：解析解（一般没有），数值解（matlab可求）。
• **微分建模思想：微元法捕捉真实变化情况。有以下几个关键点。
  • 选择合适变量
  • 分析影响因素
  • 参数范围确定
• 数值解求法：
  1. 网络剖分
  2. 离散化

九、关于线性和非线性的使用

• 大多数情况会建立一个非线性模型，部分非线性模型可以转化为线性模型。
• 非线性模型转化为线性模型后拟合时可能导致部分数据误差较大，这个时候更适合使用非线性拟合，非线性拟合时，可以用线性模型得到的参数作为迭代初始值。参考《姜起源建模341页》
• 遗传算法的直观理解：

  x = ga(fitnessfcn,nvars)
  x = ga(fitnessfcn,nvars,A,b)
  x = ga(fitnessfcn,nvars,A,b,Aeq,beq)
  x = ga(fitnessfcn,nvars,A,b,Aeq,beq,LB,UB)
  x = ga(fitnessfcn,nvars,A,b,Aeq,beq,LB,UB,nonlcon)
  x = ga(fitnessfcn,nvars,A,b,Aeq,beq,LB,UB,nonlcon,options)
  x = ga(fitnessfcn,nvars,A,b,[],[],LB,UB,nonlcon,IntCon)
  x = ga(fitnessfcn,nvars,A,b,[],[],LB,UB,nonlcon,IntCon,options)
  x = ga(problem)
  [x,fval] = ga(fitnessfcn,nvars,...)
  [x,fval,exitflag] = ga(fitnessfcn,nvars,...)
  [x,fval,exitflag,output] = ga(fitnessfcn,nvars,...)
  [x,fval,exitflag,output,population] = ga(fitnessfcn,nvars,...)
  [x,fval,exitflag,output,population,scores] = ga(fitnessfcn,nvars,...)
  

十、统计回归

• 数据分析：
  • 估计(density函数)
    $$F(x)=\frac{(X\le x)}{X}$$
  • 比较（假设检验）
    使用SPSS进行假设检验
  • 预处理（变形，分类或聚类）
  • 影响因素分析（假设检验，是否引入新变量）
  • 预测（回归、机器学习）

• 方差分析用于分析多组数据的均值有无显著差异