K-means和K-means++的算法原理及sklearn库中参数解释、选择

前言：

　　这篇博文主要介绍k-means聚类算法的基本原理以及它的改进算法k-means的原理及实现步骤，同时文章给出了sklearn机器学习库中对k-means函数的使用解释和参数选择。

K-means介绍：

　　K-means算法是很典型的基于距离的聚类算法，采用距离 作为相似性的评价指标，即认为两个对象的距离越近，其相似度就越大。该算法认为簇是由距离靠近的对象组成的，因此把得到紧凑且独立的簇作为最终目标。
　　k-means算法特点在于：同一聚类的簇内的对象相似度较高；而不同聚类的簇内的对象相似度较小。
　　

算法实现过程：

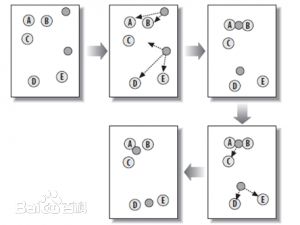
　1、随机在图中取K（这里K=2）个种子点。
　2、然后对图中的所有点求到这K个种子点的距离，假如点Pi离种子点Si最近，那么Pi属于Si点群。（上图中，我们可以看到A,B属于上面种子的点群，C,D,E属于下面种子的点群）
　3、接下来，我们要移动种子点到属于他的“点群”的中心。（见图上的第三步），这里求中心的方法最简单的是直接将中心定为点群各个坐标的平均值 ，也可以参考下面三种求中心的方法。
　4、然后重复第2）和第3）步，直到，种子点没有移动（我们可以看到图中的第四步上面的种子点聚合了A,B,C，下面的种子点聚合了D，E）。
　

求聚类中心的另外三种方法：

（1）Minkowski Distance 公式 —— λ 可以随意取值，可以是负数，也可以是正数，或是无穷大。

（2）Euclidean Distance 公式 —— 也就是第一个公式 λ=2 的情况

（3）CityBlock Distance 公式 —— 也就是第一个公式 λ=1 的情况

这三个公式的求中心点有一些不一样的地方，这三个方法逼近中心的方式不太一样，第一种以星形的方式，第二种以同心圆的方式，第三种以菱形的方式。

－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－

k-means 优缺点：

K-Means聚类算法的优点主要集中在:
　1.算法快速、简单;
　2.对大数据集有较高的效率并且是可伸缩性的;
　3.时间复杂度近于线性，而且适合挖掘大规模数据集。K-Means聚类算法的时间复杂度是O(n×k×t) ,其中n代表数据集中对象的数量，t代表着算法迭代的次数，k代表着簇的数目　

k-means的缺点：
　　1、在 K-means 算法中 K 是事先给定的，这个 K 值的选定是非常难以估计的。很多时候，事先并不知道给定的数据集应该分成多少个类别才最合适。
　　2、 在 K-means 算法中，首先需要根据初始聚类中心来确定一个初始划分，然后对初始划分进行优化。这个初始聚类中心的选择对聚类结果有较大的影响，一旦初始值选择的不好，可能无法得到有效的聚类结果，这也成为 K-means算法的一个主要问题。
　　3、从 K-means 算法框架可以看出，该算法需要不断地进行样本分类调整，不断地计算调整后的新的聚类中心，因此当数据量非常大时，算法的时间开销是非常大的。所以需要对算法的时间复杂度进行分析、改进，提高算法应用范围。
　　
对于上述的初始聚类中心的选择可以用k-means++来解决：

k-means ++介绍：

k-means++算法选择初始seeds的基本思想就是：初始的聚类中心之间的相互距离要尽可能的远。

算法步骤：
（1）从输入的数据点集合中随机选择一个点作为第一个聚类中心
（2）对于数据集中的每一个点x，计算它与最近聚类中心(指已选择的聚类中心)的距离D(x)
（3）选择一个新的数据点作为新的聚类中心，选择的原则是：D(x)较大的点，被选取作为聚类中心的概率较大
（4）重复2和3直到k个聚类中心被选出来
（5）利用这k个初始的聚类中心来运行标准的k-means算法

　　从上面的算法描述上可以看到，算法的关键是第3步，如何将D(x)反映到点被选择的概率上，一种算法如下：
（1）先从我们的数据库随机挑个随机点当“种子点”
（2）对于每个点，我们都计算其和最近的一个“种子点”的距离D(x)并保存在一个数组里，然后把这些距离加起来得到Sum(D(x))。
（3）然后，再取一个随机值，用权重的方式来取计算下一个“种子点”。这个算法的实现是，先取一个能落在Sum(D(x))中的随机值Random，然后用Random -= D(x)，直到其<=0，此时的点就是下一个“种子点”。
（4）重复2和3直到k个聚类中心被选出来
（5）利用这k个初始的聚类中心来运行标准的k-means算法
可以看到算法的第三步选取新中心的方法，这样就能保证距离D(x)较大的点，会被选出来作为聚类中心了。至于为什么原因比较简单，如下图 所示：

假设A、B、C、D的D(x)如上图所示，当算法取值Sum(D(x))*random时，该值会以较大的概率落入D(x)较大的区间内，所以对应的点会以较大的概率被选中作为新的聚类中心。

sklearn.cluster.KMeans 参数介绍

为什么要介绍sklearn这个库里的kmeans？
　　这个是现在python机器学习最流行的集成库，同时由于要用这个方法，直接去看英文文档既累又浪费时间、效率比较低，所以还不如平时做个笔记、打个基础。
　　这里还有一个原因，上面介绍了k-means++，sklearn.cluster.KMeans这个类对于初始聚类中心的选择刚好默认选择的就是k-means ++。

参数：

n_clusters：整形，缺省值=8 【生成的聚类数，即产生的质心（centroids）数。】
max_iter：整形，缺省值=300
执行一次k-means算法所进行的最大迭代数。
n_init：整形，缺省值=10
用不同的质心初始化值运行算法的次数，最终解是在inertia意义下选出的最优结果。
init：有三个可选值：’k-means++’， ‘random’，或者传递一个ndarray向量。
此参数指定初始化方法，默认值为 ‘k-means++’。
（１）‘k-means++’ 用一种特殊的方法选定初始质心从而能加速迭代过程的收敛（即上文中的k-means++介绍）
（２）‘random’ 随机从训练数据中选取初始质心。
（３）如果传递的是一个ndarray，则应该形如 (n_clusters, n_features) 并给出初始质心。
precompute_distances：三个可选值，‘auto’，True 或者 False。
预计算距离，计算速度更快但占用更多内存。
（１）‘auto’：如果 样本数乘以聚类数大于 12million 的话则不预计算距离。This corresponds to about 100MB overhead per job using double precision.
（２）True：总是预先计算距离。
（３）False：永远不预先计算距离。
tol：float形，默认值= 1e-4　与inertia结合来确定收敛条件。
n_jobs：整形数。　指定计算所用的进程数。内部原理是同时进行n_init指定次数的计算。
（１）若值为 -1，则用所有的CPU进行运算。若值为1，则不进行并行运算，这样的话方便调试。
（２）若值小于-1，则用到的CPU数为(n_cpus + 1 + n_jobs)。因此如果 n_jobs值为-2，则用到的CPU数为总CPU数减1。
random_state：整形或 numpy.RandomState 类型，可选
用于初始化质心的生成器（generator）。如果值为一个整数，则确定一个seed。此参数默认值为numpy的随机数生成器。
copy_x：布尔型，默认值=True
当我们precomputing distances时，将数据中心化会得到更准确的结果。如果把此参数值设为True，则原始数据不会被改变。如果是False，则会直接在原始数据
上做修改并在函数返回值时将其还原。但是在计算过程中由于有对数据均值的加减运算，所以数据返回后，原始数据和计算前可能会有细小差别。

属性：

cluster_centers_：向量，[n_clusters, n_features] (聚类中心的坐标)

Labels_: 每个点的分类
inertia_：float形
每个点到其簇的质心的距离之和。

Notes：
　　这个k-means运用了 Lioyd’s 算法,平均计算复杂度是 O(k*n*T)，其中n是样本量，T是迭代次数。
　　计算复杂读在最坏的情况下为 O(n^(k+2/p))，其中n是样本量，p是特征个数。(D. Arthur and S. Vassilvitskii, ‘How slow is the k-means method?’ SoCG2006）
　　在实践中，k-means算法时非常快的，属于可实践的算法中最快的那一类。但是它的解只是由特定初始值所产生的局部解。所以为了让结果更准确真实，在实践中要用不同的初始值重复几次才可以。

Methods：

fit(X[,y]):
　计算k-means聚类。
fit_predictt(X[,y]):
　计算簇质心并给每个样本预测类别。
fit_transform(X[,y])：
计算簇并 transform X to cluster-distance space。
get_params([deep])：
　取得估计器的参数。
predict(X):predict(X)
　给每个样本估计最接近的簇。
score(X[,y]):
　计算聚类误差
set_params(**params):
　为这个估计器手动设定参数。
transform(X[,y]): 将X转换为群集距离空间。
　在新空间中，每个维度都是到集群中心的距离。 请注意，即使X是稀疏的，转换返回的数组通常也是密集的。

参考文献：

1、http://blog.csdn.net/loadstar_kun/article/details/39450615
2、http://blog.csdn.net/xiaoyi_zhang/article/details/52269242