机器学习中的常见问题——损失函数

一、分类算法中的损失函数

在分类算法中，损失函数通常可以表示成损失项和正则项的和，即有如下的形式：

J(w)=∑iL(mi(w))+λR(w)

其中， L(mi(w)) 为损失项， R(w) 为正则项。 mi 的具体形式如下：

mi=y(i)fw(x(i))

y(i)∈{−1,1}

fw(x(i))=wTx(i)

对于损失项，主要的形式有：

• 0-1损失
• Log损失
• Hinge损失
• 指数损失
• 感知损失

1、0-1损失函数

在分类问题中，可以使用函数的正负号来进行模式判断，函数值本身的大小并不是很重要，0-1损失函数比较的是预测值 fw(x(i)) 与真实值 y(i) 的符号是否相同，0-1损失的具体形式如下：

L01(m)={01 if m⩾0 if m<0

以上的函数等价于下述的函数：

12(1−sign(m))

0-1损失并不依赖 m 值的大小，只取决于 m 的正负号。0-1损失是一个非凸的函数，在求解的过程中，存在很多的不足，通常在实际的使用中将0-1损失函数作为一个标准，选择0-1损失函数的代理函数作为损失函数。

2、Log损失函数

2.1、Log损失

Log损失是0-1损失函数的一种代理函数，Log损失的具体形式如下：

log(1+exp(−m))

运用Log损失的典型分类器是Logistic回归算法。

2.2、Logistic回归算法的损失函数

对于Logistic回归算法，分类器可以表示为：

p(y∣x;w)=σ(wTx)y(1−σ(wTx))(1−y)

其中， y∈{0,1} 。为了求解其中的参数 w ，通常使用极大似然估计的方法，具体的过程如下：

1、似然函数

L(w)=∏i=1nσ(wTx(i))y(i)(1−σ(wTx(i)))(1−y(i))

其中，

σ(x)=11+exp(−x)

2、log似然

logL(w)=∑i=1ny(i)log(σ(wTx(i)))+(1−y(i))log(1−σ(wTx(i)))

3、需要求解的是使得log似然取得最大值的 w ，可以转换为求最小值：

−logL(w)=−∑i=1ny(i)log(σ(wTx(i)))+(1−y(i))log(1−σ(wTx(i)))

这便是交叉熵的具体形式。

2.3、两者的等价

由于Log损失的具体形式为：

log(1+exp(−m))

其中， m=y(i)wTx(i) ， y(i)∈{−1,1} ，Log损失函数的具体形式为：

minw∑i=1nlog{1+exp(−y(i)wTx(i))}

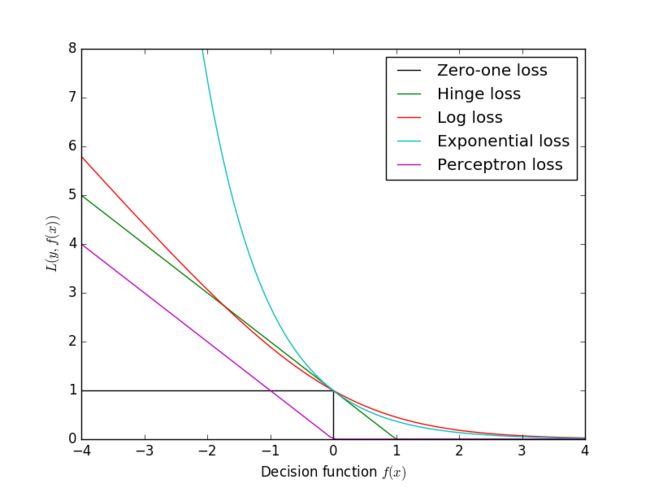
Logistic回归与Log损失具有相同的形式，故两者是等价的。Log损失与0-1损失的关系可见下图。

3、Hinge损失函数

3.1、Hinge损失

Hinge损失是0-1损失函数的一种代理函数，Hinge损失的具体形式如下：

max(0,1−m)

运用Hinge损失的典型分类器是SVM算法。

3.2、SVM的损失函数

对于软间隔支持向量机，允许在间隔的计算中出现少许的误差 ξ⃗ =(ξ1,⋯,ξn) ，其优化的目标为：

minw,γ,ξ[12∥w∥2+C∑i=1nξi]

约束条件为：

(wTx(i)+γ)y(i)⩾1−ξi,ξi≥0

3.3、两者的等价

对于Hinge损失：

max(0,1−m)

优化的目标是要求：

minw[∑i=1nmax(0,1−fw(x(i))y(i))]

在上述的函数 fw(x(i)) 中引入截距 γ ，即：

fw,γ(x(i))=wTx(i)+γ

并在上述的最优化问题中增加 L2 正则，即变成：

minw,γ[C∑i=1nmax(0,1−fw,γ(x(i))y(i))+12∥w∥2]

至此，令下面的不等式成立：

max(0,1−fw,γ(x)y)=minξξ

约束条件为：

ξ⩾1−fw,γ(x)y;ξ⩾0

则Hinge最小化问题变成：

minw,γ,ξ[C∑i=1nξi+12∥w∥2]

约束条件为：

ξi⩾1−(wTx(i)+γ)y(i);ξi⩾0

这与软间隔的SVM是一致的，说明软间隔SVM是在Hinge损失的基础上增加了 L2 正则。

4、指数损失

4.1、指数损失

指数损失是0-1损失函数的一种代理函数，指数损失的具体形式如下：

exp(−m)

运用指数损失的典型分类器是AdaBoost算法。

4.2、AdaBoost基本原理

AdaBoost算法是对每一个弱分类器以及每一个样本都分配了权重，对于弱分类器 φj 的权重为：

θj=12log1−R(φj)R(φj)

其中， R(φj) 表示的是误分类率。对于每一个样本的权重为：

wi=exp(−f(x(i)y(i)))∑n[exp(−f(x(i)y(i)))]

最终通过对所有分类器加权得到最终的输出。

4.3、两者的等价

对于指数损失函数：

exp(−m)

可以得到需要优化的损失函数：

minθ[∑i=1nexp(−fθ(x(i))y(i))]

假设 f~ 表示已经学习好的函数，则有：

minθ,φ[∑i=1nexp(−{f~θ(x(i))+θφ(x(i))}y(i))]

=minθ,φ[∑i=1nwi~exp(−θφ(x(i))y(i))]

而：

∑i=1nwi~exp(−θφ(x(i))y(i))={exp(θ)−exp(−θ)}∑i=1nwi~2(1−φ(x(i))y(i))+exp(−θ)∑i=1nwi~

通过最小化 φ ，可以得到：

φ^=argminφ∑i=1nw~i2(1−φ(x(i))y(i))

将其代入上式，进而对 θ 求最优解，得：

θ^=12log1−R^R^

其中，

R^={∑i=1nw~i2(1−φ(x(i))y(i))}/{∑i=1nw~i}

可以发现，其与AdaBoost是等价的。

5、感知损失

5.1、感知损失

感知损失是Hinge损失的一个变种，感知损失的具体形式如下：

max(0,−m)

运用感知损失的典型分类器是感知机算法。

5.2、感知机算法的损失函数

感知机算法只需要对每个样本判断其是否分类正确，只记录分类错误的样本，其损失函数为：

minw,b[−∑i=1ny(i)(wTx(i)+b)]

5.3、两者的等价

对于感知损失：

max(0,−m)

优化的目标为：

minw[∑i=1nmax(0,−fw(x(i))y(i))]

在上述的函数 fw(x(i)) 中引入截距 b ，即：

fw,γ(x(i))=wTx(i)+b

上述的形式转变为：

minw,b[∑i=1nmax(0,−(wTx(i)+b)y(i))]

对于max函数中的内容，可知：

max(0,−(wTx(i)+b)y(i))⩾0

对于错误的样本，有：

max(0,−(wTx(i)+b)y(i))=−(wTx(i)+b)y(i)

类似于Hinge损失，令下式成立：

max(0,−fw,b(x)y)=minξξ

约束条件为：

ξ⩾−fw,b(x)y

则感知损失变成：

minξ[∑i=1nξi]

即为：

minw,b[−∑i=1ny(i)(wTx(i)+b)]

Hinge损失对于判定边界附近的点的惩罚力度较高，而感知损失只要样本的类别判定正确即可，而不需要其离判定边界的距离，这样的变化使得其比Hinge损失简单，但是泛化能力没有Hinge损失强。

import matplotlib.pyplot as plt
import numpy as np

xmin, xmax = -4, 4
xx = np.linspace(xmin, xmax, 100)
plt.plot([xmin, 0, 0, xmax], [1, 1, 0, 0], 'k-', label="Zero-one loss")
plt.plot(xx, np.where(xx < 1, 1 - xx, 0), 'g-', label="Hinge loss")
plt.plot(xx, np.log2(1 + np.exp(-xx)), 'r-', label="Log loss")
plt.plot(xx, np.exp(-xx), 'c-', label="Exponential loss")
plt.plot(xx, -np.minimum(xx, 0), 'm-', label="Perceptron loss")

plt.ylim((0, 8))
plt.legend(loc="upper right")
plt.xlabel(r"Decision function $f(x)$")
plt.ylabel("$L(y, f(x))$")
plt.show()

参考文章

• Advice for applying Machine Learning