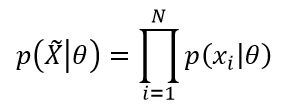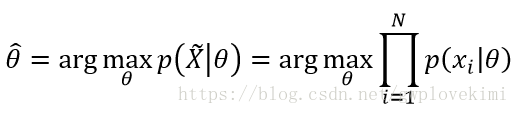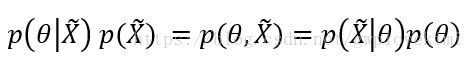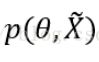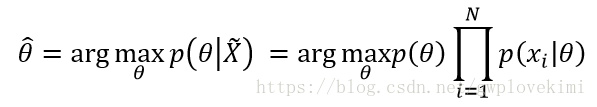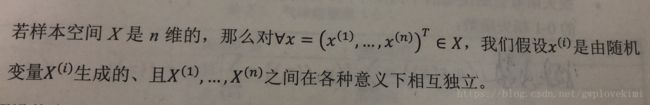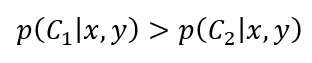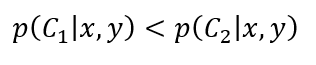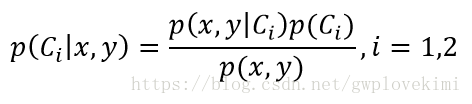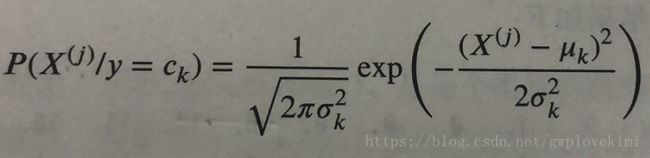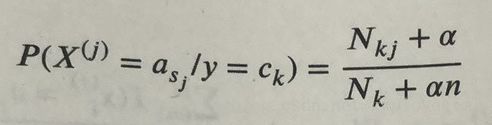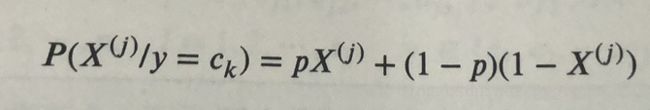机器学习笔记之（2）——贝叶斯分类器

本博客为本人学习贝叶斯分类器的学习笔记。由于仅仅是学习笔记，水平有限，还望广大读者朋友多多赐教。好，话不多说，直接进入正题。

贝叶斯分类器其实就是基于贝叶斯决策理论的分类器。贝叶斯理论在大一的必修课概率论里面学过。一句话概况就是后验概率取决于先验概率与类条件概率密度。贝叶斯理论也是卡尔曼滤波理论的基础（后续我也打算再写一个卡尔曼滤波或粒子滤波方面的学习笔记）

贝叶斯学派与频率学派

首先介绍统计学里面的两个学派：频率学派与贝叶斯学派。

• 频率学派：强调概率的“客观性”，概率为客观随机性。模型参数固定，样本随机。认为观察者获得的信息是一样的。认为应该将事件在重复试验中发生的频率作为其发生的概率的估计。
• 贝叶斯学派：强调概率的“主观性”，即条件概率。样本固定，模型参数视为关键。认为不同的观察者获得的信息是不一样的。认为事情发生概率的客观性仅仅是因为观察者不知道事件的结果。随机性的根源不在于事件，而在于观察者对事件的知识状态。而频率学派则认为随机性的根源就是事件，跟观察者无关。

贝叶斯决策是在某个先验分布下，使得平均风险最小的决策。

条件概率：

参数估计

即从已有的样本中获取信息，并根据此信息估计目标模型的参数。（比如基于大数定律的频率近似概率模型）

极大似然估计（ML估计）

认为待估计的模型的参数固定且未知。把模型描述成概率模型，希望得到的模型参数能够使得在训练集作为输入时，模型输出的概率达极大。

通俗理解：有这样的模型，就会输出这样的数据，而当将模型看作概率，以数据为输入时，则当概率达到最大时，可估计出模型参数。

也即在模型参数为时能够输出数据的概率为：

希望找到的（估计的）模型参数，就是使得似然函数在以作为输入时达到极大的参数（似然函数）：

极大似然估计把待估计参数看作一个未知但固定的量，不考虑观察者的影响（即不考虑先验知识的影响），属于频率学派。

极大后验概率估计（MAP估计）

属于贝叶斯学派。将待估计参数看作一个随机变量，从而引入了参数的先验分布。

后验概率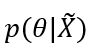——可以理解为参数在训练集下所谓的“真实出现的概率”，能够利用参数的先验概率、样本的先验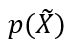概率和条件概率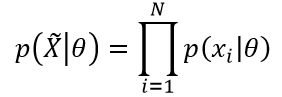通过贝叶斯公式推导出：

其中，为联合概率

MAP的似然函数与ML的区别就是引入了参数的先验分布

朴素贝叶斯

朴素贝叶斯在估计参数时采用了极大似然估计，而在决策时采用了极大后验概率估计。而贝叶斯决策则是在某个先验分布下使得平均风险最小的决策。

“朴素”一词是指：独立性假设，即特征之间相互独立。而所谓的独立，是指一个特征的出现的可能性与其他特征没有关系，且每个特征同等重要。“贝叶斯”一词指：后验概率最大化的决策标准。

所谓的独立性假设指：

贝叶斯决策理论（后验概率最大化决策标准）

对于一个样本点（假设有两个特征x和y），那么这个样本点属于类别1的概率为P1(x,y)，属于类别2的概率为P2(x,y)。（假设为 二分类），那么贝叶斯决策理论为：

• 如果P1(x,y)>P2(x,y)，那么该样本点类别为1。
• 如果P1(x,y)

也即最高概率决策。上面式子只是为了直观表达，而实际上，应该是：

时，为类别1。

时，为类别2。

且根据贝叶斯公式有：

由于在此公式中为常数，所以一般贝叶斯决策时，都说后验概率由先验概率（先验知识）与类条件概率密度所决定。

贝叶斯分类器

用贝叶斯决策作为分类的分类器称为贝叶斯分类器。通过某个对象的先验概率，利用贝叶斯公式计算出其后验概率，即该对象属于某一类别的概率，选择具有最大后验概率的类作为该对象所属的类。

在朴素贝叶斯分类器中，要学习的参数为：先验概率和类条件概率密度。

在scikit-learn中有以下三种常用的朴素贝叶斯分类器，它们的主要区别在于假设了不同的类条件概率密度分布的形式：

1、GaussianNB，高斯贝叶斯分类器。它假设特征的条件概率分布满足高斯分布：

2、MultinomialNB，多项式贝叶斯分类器。它假设特征的条件概率分布满足多项式分布：

3、BernoulliNB，伯努利贝叶斯分布。它假设特征的条件概率满足二项式分布：

多项式和伯努利模型都是适用于离散特征的情况。

其实，对于贝叶斯理论应该给出比较多的公式推导以及分析，但是限于本人的水平有限，在这里就先不介绍详细的理论，只是很浅显的给出了一些基本理论（后面如果本人更好的理解整套贝叶斯理论数学推导的方法，会及时更新到博客上来哈~），接下来，直接看代码吧

给出Python代码如下：

from sklearn import datasets,cross_validation, naive_bayes


###############################################################################
#使用的数据集为scikit-learn自带的手写识别数据集,加载数据集
def load_data():
    digits=datasets.load_digits()
    return cross_validation.train_test_split(digits.data,digits.target,test_size=0.25,random_state=0)
    #返回为: 一个元组，依次为：训练样本集、测试样本集、训练样本的标记、测试样本的标记 
    #cross_validation为分层采用，分层采样保证了测试样本集中各类别样本的比例与原始样本集中各类别样本的比例相同
    


###############################################################################
#定义高斯贝叶斯分类器函数。高斯贝叶斯分类器没有参数，因此不需要调参
def test_GaussianNB(*data):
    x_train,x_test,y_train, y_test=data
    cls=naive_bayes.GaussianNB()
    cls.fit(x_train,y_train)
    print('高斯贝叶斯分类器')
    print('Training Score: %.2f' % cls.score(x_train,y_train))
    print('Testing Score: %.2f' % cls.score(x_test, y_test))



###############################################################################
#多项式贝叶斯分类器
def test_MultinomialNB(*data):
    x_train,x_test,y_train, y_test=data
    cls=naive_bayes.MultinomialNB()
    cls.fit(x_train,y_train)
    print('多项式贝叶斯分类器')
    print('Training Score: %.2f' % cls.score(x_train,y_train))
    print('Testing Score: %.2f' % cls.score(x_test, y_test))
    
    
    
###############################################################################
#伯努利贝叶斯分类器
def test_BernoulliNB(*data):
    x_train,x_test,y_train, y_test=data
    cls=naive_bayes.BernoulliNB()
    cls.fit(x_train,y_train)
    print('伯努利贝叶斯分类器')
    print('Training Score: %.2f' % cls.score(x_train,y_train))
    print('Testing Score: %.2f' % cls.score(x_test, y_test))
    
    
    
###############################################################################
x_train,x_test,y_train, y_test=load_data()
test_GaussianNB(x_train,x_test,y_train, y_test)
test_MultinomialNB(x_train,x_test,y_train, y_test)
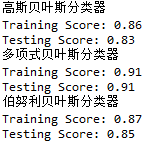
test_BernoulliNB(x_train,x_test,y_train, y_test)

结果如下图所示：

进一步地，查看scikit-learn自带的手写识别数据集，这里只是绘制数据集中前 25 个样本的图片：

from sklearn import datasets
import matplotlib.pyplot as plt



###############################################################################
#使用的数据集为scikit-learn自带的手写识别数据集,通过下面函数来观察数据集
def show_digits():
    digits=datasets.load_digits()
    fig=plt.figure()
    print("查看图片0的向量",digits.data[0])
    
    #输出25张图片
    for i in range(25):
        ax=fig.add_subplot(5,5,i+1)
        ax.imshow(digits.images[i],cmap=plt.cm.gray_r,interpolation='nearest')
    plt.show()
    


###############################################################################
show_digits()

结果为：

对于函数add_subplot()，作用为：

好，贝叶斯分类器的学习笔记先到这~后续有新的关于贝叶斯分类器的体会会更新到这里，也希望能与广大读者多多交流

参考资料~仍然是下面的这几本书：

• 《机器学习实战》
• 《Python机器学习》
• 《机器学习Python实践》
• 《Python机器学习算法》
• 《Python大战机器学习》
• 《Python与机器学习实战》