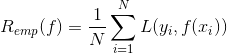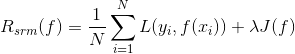统计学习方法概述(模型、策略、算法)
主要内容(只考虑监督学习)
(1)统计学习三要素概述
(2)理解目标函数、代价函数、损失函数
(3)理解经验风险、结构风险(正则化)
-------------------------------------------------------------------------------------------------------------------------
一、统计学习方法概述
统计学习三要素:方法 = 模型+策略+算法
1、模型
在监督学习过程中,模型就是要学习条件概率分布或决策函数,模型假设空间包含所有可能的条件概率分布或决策函数(假设空间内的模型有无穷个),函数空间内通常由一个参数向量决定函数族,参数向量![]() 取值于n维欧式空间
取值于n维欧式空间![]() ,称为参数空间。
,称为参数空间。
![]()
2、策略
策略就是按照什么样的规则选择或学习最优的模型。在监督学习中,就是在假设空间![]() 中选择最优模型
中选择最优模型![]() 作为决策函数。
作为决策函数。
损失函数:度量模型一次预测的好坏
风险函数:度量平均意义下模型预测的好坏
对于给定的![]() ,由
,由![]() 给出相应的输出Y,这个输出的预测值
给出相应的输出Y,这个输出的预测值![]() 与真实值Y可能一致可能不一致,在此,用一个损失函数或代价函数来度量预测错误的程度,记作
与真实值Y可能一致可能不一致,在此,用一个损失函数或代价函数来度量预测错误的程度,记作![]() ,常用的损失函数(代价函数):
,常用的损失函数(代价函数):
(1)0-1损失
(2)平方损失
![]()
(3)绝对损失函数
![]()
(4)对数损失函数或对数似然损失函数
![]()
演进过程
(a)关键词:期望风险、经验风险
学习的目标(策略):选择期望风险最小的模型
期望风险:![]()
期望风险![]() 是模型关于联合分布的期望损失,经验风险
是模型关于联合分布的期望损失,经验风险![]() 是模型关于训练样本集的平均损失。
是模型关于训练样本集的平均损失。
其中,![]() 是关于联合分布
是关于联合分布![]() 的,但实际上由于
的,但实际上由于![]() 是未知的,
是未知的,![]() 是不能计算的(若知道
是不能计算的(若知道![]() ,则可直接求出条件概率分布
,则可直接求出条件概率分布![]() ,也就没必要学习模型了)。故正因为不知道
,也就没必要学习模型了)。故正因为不知道![]() ,所以需要学习模型。
,所以需要学习模型。
思路:根据大数定律,当样本容量N趋于无穷时,经验风险趋于期望风险。也就是用经验风险估计期望风险。
问题:由于现实中样本有限,用经验风险估计期望风险往往不理想,因此需要对经验风险进行矫正,则出现两个策略:经验风险最小化和结构风险最小化
(b)关键词:经验风险最小化、结构风险最小化
最优模型:经验风险最小的模型
当样本足够大时,经验风险最小化能保证有很好的效果(如极大似然估计),但是当样本容量很小时,经验风险最小化学习样本未必很好,会产生过拟合。因此,提出了结构风险最小化(等价于正则化),结构风险也就是在经验风险上加上表示模型复杂度的正则化项或罚项
其中,![]() 为模型的复杂度,模型
为模型的复杂度,模型![]() 越复杂,复杂度
越复杂,复杂度![]() 就越大,反之成立。
就越大,反之成立。![]() 是系数,用以权衡经验风险和模型复杂度。结构等闲小需要经验风险和模型复杂度同时小,这样才能保证有较好的预测效果。
是系数,用以权衡经验风险和模型复杂度。结构等闲小需要经验风险和模型复杂度同时小,这样才能保证有较好的预测效果。
结论:监督学习问题变成经验风险或结构风险函数最优化问题
3、算法
算法是指学习模型的具体计算方法,统计学习基于训练数据集,根据学习策略,从假设空间中选择最优模型,最后需要考虑用什么样的计算方法求解最优模型。
二、案例说明
1、流程
(1)损失函数、代价函数、目标函数
损失函数 = 代价函数,目标函数是一个与之相关但更广的概念,对于目标函数来说在有约束条件下的最小化就是损失函数。
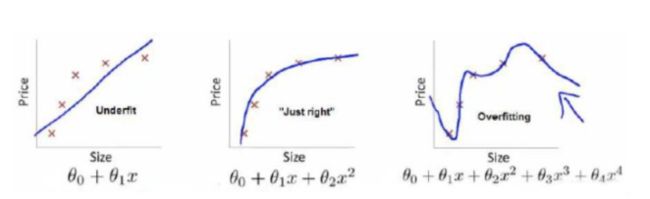
上面三张图的函数分别为![]() 、
、![]() 、
、![]() 。分别采用三个函数来拟合Price,其真实值为Y。
。分别采用三个函数来拟合Price,其真实值为Y。
对于给定的x,预测的![]() 可能与Y相同,也有可能不同,为了衡量拟合效果的好坏,采用
可能与Y相同,也有可能不同,为了衡量拟合效果的好坏,采用![]() 损失函数(代价函数)量化。损失函数越小,拟合效果越好。
损失函数(代价函数)量化。损失函数越小,拟合效果越好。
问题:难道损失函数越小越好嘛?当然不是!
(2)经验风险、期望风险
风险函数是损失函数的期望(经验风险),是关于训练集的平均损失,目标就是经验风险最小化
问题:经验风险越小越好嘛?当然不是!
(3)结构风险
如果经验风险最小化,则 ![]() 当然是经验风险函数最小了,但这明显是过拟合了。
当然是经验风险函数最小了,但这明显是过拟合了。
不仅要让经验风险最小化,还要让结构风险最小化,也就定义了一个函数![]() ,专门用来模型复杂度的,在机器学习中称作正则化,常用的有L1,L2范数。
,专门用来模型复杂度的,在机器学习中称作正则化,常用的有L1,L2范数。
目标函数:最优化经验风险和结构风险
结论:
![]() 结构风险最小(模型复杂度最低),但是经验风险最大(拟合效果差)
结构风险最小(模型复杂度最低),但是经验风险最大(拟合效果差)
![]() 结构风险和经验风险较好(拟合效果好)
结构风险和经验风险较好(拟合效果好)
![]() 结构风险最大(模型复杂度最高),但是经验风险最小(拟合效果最差)
结构风险最大(模型复杂度最高),但是经验风险最小(拟合效果最差)
参考李航《统计学习方法》和 https://blog.csdn.net/ganzhantoulebi0546/article/details/79617642
注:以上内容属个人理解,学艺不精,请各位大神多多指教