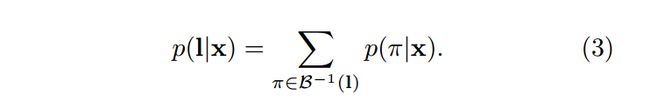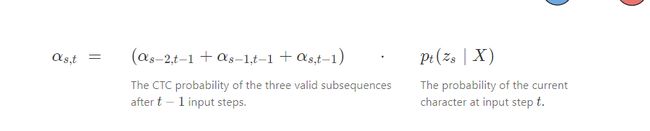关于CTC模型的理解
-
- 预备知识
- 摘要
- 标签错误率
- CTC
- 从输出到标签
- 构建分类器
- 参考资料
最近在看手势识别相关论文,在看到一篇论文的时候发现了LSTM+CTC能够解决数据预分割的问题。于是抱着学习的心态这篇论文《Connectionist Temporal Classification: Labelling Unsegmented Sequence Data with Recurrent Neural Networks》。所以本片博客的内容主要是基于论文以及斯坦福PhD的一篇博客,以及自己的一些理解。
预备知识
在看懂CTC之前需要了解隐马尔可夫模型和EM算法。其实CTC里面的思想和HMM很相似,但是又有所区别,如果搞懂了HMM,那么对于CTC的理解就会轻松很多。如果有对HMM不太懂的可以参考我前面几篇博客。
EM算法(Expectation maximization algorithm)
隐马尔科夫模型一(概念理解)
隐马尔可夫模型二(公式推导)
摘要
首先我们要搞清楚为什么要发明CTC,对于真实世界的序列学习任务,数据往往含有噪声和没有预先分割。RNN是一个强大的序列学习模型,但是需要对数据进行预先处理,所以有了CTC我们就能够提升RNN的性能。下面结合论文
标签错误率
首先文章定义了一个标签错误率(label error rate)来进行度量。其中 x x 和 z z 分别表示的是输入序列和标签序列, S′ S ′ 是一个 (x,z) ( x , z ) 的序列集合而 |S′| | S ′ | 表示序列的对数,就是里面有多少对 (x,z) ( x , z ) 。
其中 ED(p,q) E D ( p , q ) 表示编辑距离,其中 p,q p , q 表示的是两个序列。编辑距离的意思是其中 p p 经过插入删除和替换字符等基本操作转换成序列 q q 的操作数。
CTC
从输出到标签
对于一个给定长度为 T T 的输入序列 x x ,定义一个RNN。并且定义 y y 为RNN对应的输出,将 ytk y k t 定义为在 t t 时刻观测到标签 k k 的概率。并且定义了一个新的标签集合 L′=L∪{blank} L ′ = L ∪ { b l a n k } ,即在原始标签集合的基础上加上一个空白标签。
其中 π π 表示的是有RNN的输出组成的序列路径。而 πt π t 则是对应于 t t 时刻的RNN的输出,例如此时的输出为a。
接下来是定义一个多对一的映射 β β ,将输出路径映射到标签上,其中输出路径长度要大于或者等于标签长度。具体做法是通过移除路径中重复的标签和空白格。举一个简单的例子: β(a−aab−)=β(−aa−abb−)=aab β ( a − a a b − ) = β ( − a a − a b b − ) = a a b 。其实这一步涉及到输入 X=(x1,x2,..,xT) X = ( x 1 , x 2 , . . , x T ) 和输出 Y=(y1,y2,...,yM) Y = ( y 1 , y 2 , . . . , y M ) 的对齐,具体的规则其实论文里面讲解得不是很清楚,后来看参考文献2才明白具体做法。
在下图中,第一行表示的是输入x,然后将重复标签合并,并且删除空白,最后就能够得到hello
并且如果 Y Y 中同一行有两个连续并且相同的字母,表示在输入的时候两个连续字母之间一定有一个空白符 ε ε ,以l为例。接下来我们来看一些有效对齐和无效对齐。
CTC对齐有一些显著的特性。 首先,X和Y之间允许的对齐是单调的。 如果我们前进到下一个输入,我们可以保持相应的输出相同或前进到下一个输入。 第二个属性是X到Y的对齐是多对一的。 一个或多个输入元素可以对齐到一个输出元素,但反过来不成立。 这意味着第三个属性:Y的长度不能大于X的长度。
目标函数:
即对应每一步概率 pt(at|X) p t ( a t | X ) 的乘积。
然后令 l=β(π) l = β ( π ) ,最后求出求出标签对应路径的概率之和,要知道为什么这么做可以看一下HMM模型三个问题中的第三个问题。所以有:
构建分类器
这一步实际作用是解码。对于输出结果的分类应该是输入序列对应的最优可能的标签。其中 h(x) h ( x ) 表示的是分类结果,即在输入为 x x 时,最有可能的标签序列 l l 。
这一步和HMM一样,也分为两种方法,一种是Best path decoding,另一种方法是prefix search decoding。
Best path decoding是基于一个假设,最有可能的输出序列对应最有可能的标签。
其中 π∗ π ∗ 表示最有可能的路径。其实就是穷举遍历求最大值,缺点在于计算量比较大,还有可能找不到最佳结果,基于前面的假设。
prefix search decoding是基于前向后向算法的改进。其标签序列对应HMM里面的状态序列。任意状态之间是可以相互转换的,由隐马尔可夫链决定转换成功率。而标签序列是有顺序的,所以只能从一个转换到下一个,而不能从下一个状态回到上一个状态。如图所示。只能先a后b,而不能先b后a。
下面我们具体看看约束规则。
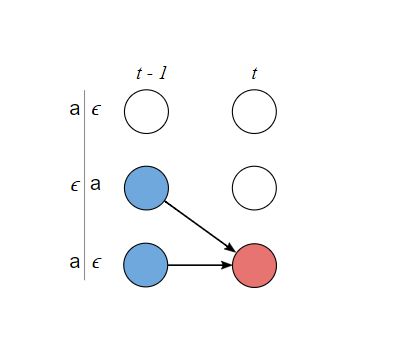
首先我们定义 αs,t α s , t 在序列中 t t 时刻出现 s s 的概率。
对于 ys=ys−2 y s = y s − 2 :
有
对于 ys−1=ε,yt2≠yt y s − 1 = ε , y t 2 ≠ y t
其实统一起来就是
上面公式就没有按照博客里面的图片,而是与论文里面保持一致。
接下来就是损失函数:
未完待续。。。
参考资料
1.Connectionist Temporal Classification: Labelling Unsegmented Sequence Data with Recurrent Neural Networks
2.Sequence Modeling With CTC
3.CTC原理