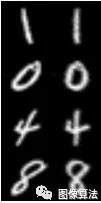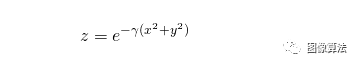如何使用OpenCV进行手写数字分类器C++/Python

在本教程中，我们将使用OpenCV构建一个简单的手写数字分类器。我们将共享用C ++和Python编写.

图像分类管道

本章节暂不讨论图像分类管道，大家可以自行搜索相关知识，下次我们补充。

 

我们将使用方向梯度直方图作为特征描述符和支持向量机（SVM）作为分类的机器学习算法。

使用OpenCV的光学字符识别（OCR）示例（C ++ / Python）

我想与代码共享一个示例，以使用HOG + SVM演示图像分类。与此同时，我希望尽可能保持简单，这样除了HOG和SVM之外我们不需要太多东西。这个灵感和数据来自OpenCV的教程在这里：

http://docs.opencv.org/trunk/dd/d3b/tutorial_py_svm_opencv.html

原始教程仅在Python中，并且由于一些奇怪的原因实现了它自己的简单HOG描述符。我们用OpenCV的HOG描述符替换了他们自己开发的HOG。

OCR的数字数据集

我们将使用上面的图像作为OpenCV样本附带的数据集。它共包含5000张图像 - 每个数字500张图像。每幅图像均为20×20灰度，背景为黑色。这些数字中的4500个将用于训练，其余500个将用于测试算法的性能。您可以点击上面的图片放大。

让我们完成构建和测试分类器所需的步骤。

第1步：纠偏（预处理）

人们通常将学习算法视为块框。在一端输入图像，在另一端输出结果。实际上，您可以稍微协助算法，并注意到性能的巨大提升。例如，如果您正在构建面部识别系统，则将图像与参考面对齐通常会导致性能的显着提高。典型的对准操作使用面部特征检测器来对准每个图像中的眼睛。

在构建分类器之前对齐数字同样会产生更好的结果。在面部的情况下，对准是相当明显的 - 您可以对面部图像应用相似变换，以将眼睛的两个角对准参考面的两个角。

歪斜的例子

在手写数字的情况下，我们没有明显的特征，如我们可以用于对齐的眼角。然而，人们写作的明显变化是他们的写作倾向。有些作者有一个向右或向前的倾斜，其中数字向前倾斜，有些具有向后或向左倾斜，有些没有倾斜。我们可以通过修复这个垂直斜面来帮助算法，因此它不必学习数字的这种变化。左侧的图像显示第一列中的原始数字，并且它是倾斜（固定）版本。

可以使用图像矩来实现对简单灰度图像的这种偏斜校正。OpenCV有一个瞬间的实现，它在计算有用的信息时很方便，如质心，面积，黑色背景的简单图像的偏斜。

事实证明，偏斜的度量是由两个中心力矩（mu11 / mu02）的比率给出的。如此计算的偏度可以用于计算对图像进行校正的仿射变换。

偏移的代码如下：

C++

Mat deskew(Mat& img)

{

Moments m = moments(img);

if(abs(m.mu02) < 1e-2)

{

// No deskewing needed.

return img.clone();

}

// Calculate skew based on central momemts.

double skew = m.mu11/m.mu02;

// Calculate affine transform to correct skewness.

Mat warpMat = (Mat_(2,3) << 1, skew, -0.5*SZ*skew, 0, 1 , 0);

Mat imgOut = Mat::zeros(img.rows, img.cols, img.type());

warpAffine(img, imgOut, warpMat, imgOut.size(),affineFlags);

return imgOut;

}

Python

def deskew(img):

m = cv2.moments(img)

if abs(m['mu02']) < 1e-2:

# no deskewing needed.

return img.copy()

# Calculate skew based on central momemts.

skew = m['mu11']/m['mu02']

# Calculate affine transform to correct skewness.

M = np.float32([[1, skew, -0.5*SZ*skew], [0, 1, 0]])

# Apply affine transform

img = cv2.warpAffine(img, M, (SZ, SZ), flags=cv2.WARP_INVERSE_MAP | cv2.INTER_LINEAR)

return img

步骤2：计算定向梯度直方图（HOG）描述符

在此步骤中，我们将使用HOG特征描述符将灰度图像转换为特征向量。

我们发现理论与实践之间存在巨大差距。获取知识很容易。我可以阅读论文和书籍。如果我们不理解这个概念或数学，我们可以阅读更多的论文和书籍。这很容易。将这些知识付诸实践的难点。部分原因是很多这些算法在繁琐的手动操作之后起作用，并且如何设置正确的参数并不明显。例如，在Harris角点检测器中，为什么自由参数k设置为0.04？为什么不是1或2或0.34212呢？为什么42是生命，宇宙和一切的答案？

随着我获得更多真实世界的经验，我意识到在某些情况下你可以做出有根据的猜测，但在其他情况下，没有人知道为什么。人们经常进行参数扫描 - 他们以原则方式改变不同的参数，以查看产生最佳结果的因素。有时，最好的参数有一个直观的解释，有时他们没有。

牢记这一点，让我们看看为我们的HOG描述符选择了哪些参数。我们也会尝试解释为什么它们有意义，但我会提供有力的手工操作而不是严格的证据！

C++

HOGDeor hog(

Size(20,20), //winSize

Size(10,10), //blocksize

Size(5,5), //blockStride,

Size(10,10), //cellSize,

9, //nbins,

1, //derivAper,

-1, //winSigma,

0, //histogramNormType,

0.2, //L2HysThresh,

1,//gammal correction,

64,//nlevels=64

1);//Use signed gradients

Python

winSize = (20,20)

blockSize = (10,10)

blockStride = (5,5)

cellSize = (10,10)

nbins = 9

derivAperture = 1

winSigma = -1.

histogramNormType = 0

L2HysThreshold = 0.2

gammaCorrection = 1

nlevels = 64

signedGradients = True

hog = cv2.HOGDeor(winSize,blockSize,blockStride,cellSize,nbins,derivAperture,winSigma,histogramNormType,L2HysThreshold,gammaCorrection,nlevels, useSignedGradients)

我们不打算来形容derivAperture，winSigma，histogramNormType，L2HysThreshold，伽玛校正和NLEVELS，因为我从来没有在使用HOG描述符来改变这些参数。除非您仔细阅读原始HOG文件，否则我建议您使用默认值。让我们探讨其他参数的选择。

winSize：此参数设置为20×20，因为我们的数据集中的数字图像的大小是20×20，我们想要为整个图像计算一个描述符。

cellSize：我们的数字是20×20灰度图像。换句话说，我们的图像由20×20 = 400个数字表示。描述符的大小通常远小于图像中的像素数。基于进行分类的重要特征的尺度来选择cellSize。一个非常小的cellSize会炸掉特征向量的大小，而一个非常大的cellSize可能无法捕获相关信息。您应该使用本文中共享的代码自行测试。我们在本教程中选择了10×10的cellSize。我们可以选择8吗？是的，那也行得通。

blockSize：块的概念存在以解决照明变化。较大的块大小使本地更改不太重要，而较小的块大小权重本地更改更多。通常，blockSize设置为2 x cellSize，但在我们的数字分类示例中，照明并不是一个挑战。在我的实验中，10×10的blockSize给出了最好的结果。

blockStride：blockStride确定相邻块之间的重叠并控制对比度标准化程度。通常，blockStride设置为blockSize的50％。

nbins：nbins设置渐变直方图中的bin数。HOG论文的作者建议使用值9来捕获0到180度之间的渐变，以20度为增量。在我的实验中，将此值增加到18并没有产生任何更好的结果。

signedGradients：通常，渐变可以具有0到360度之间的任何方向。这些梯度被称为“有符号”梯度，而不是“无符号”梯度，它们使符号下降并取0到180度之间的值。在原始HOG纸中，无符号梯度用于行人检测。在我的实验中，对于这个问题，签名渐变产生了稍好的结果。

上面定义的HOG描述符可用于使用以下代码计算图像的HOG特征。

C++

// im is of type Mat

vector deors;

hog.compute(im,deor);

Python

deor = hog.compute(im)

对于我们选择的参数，该描述符的大小为81×1。

第3步：训练模型（又称学习分类器）

在此之前，我们已经对原始图像进行了校正，并为我们的图像定义了描述符。这使我们能够将数据集中的每个图像转换为大小为81×1的向量。

我们现在准备训练一个模型，对我们训练集中的图像进行分类。为此，我们选择了支持向量机（SVM）作为我们的分类算法。虽然SVM背后的理论和数学涉及并超出了本教程的范围，但它的工作原理非常直观且易于理解。您可以查看我之前解释线性SVM的帖子。

要快速回顾一下，如果在n维空间中有点并且类标签附加到点，则线性SVM将使用平面划分空间，使得不同的类位于平面的不同侧。在下图中，我们有两个由红色和蓝色圆点表示的类。如果将此数据输入到线性SVM中，则可以通过查找明确区分这两个类的行来轻松构建分类器。有许多行可以分离这些数据。SVM选择处于任一类的最大距离数据点的那个。

与我们的数字分类问题相比，上图中显示的两类示例可能看起来很简单，但在数学上它们非常相似。我们的图像描述符不是二维空间中的点，而是81维空间中的点，因为它们由81×1向量表示。附加到这些点的类标签是图像中包含的数字，即0,1,2，... 9.而不是2D中的线，SVM将在高维空间中找到超平面来进行分类。

SVM参数C.

在训练SVM时您需要了解的两个常见参数之一称为C.真实世界数据不像上面所示那样干净。有时，训练数据可能有错误标记的示例。在其他时候，一组的一个例子在外观上可能与另一个例子太接近。例如，手写数字2可能看起来像3。

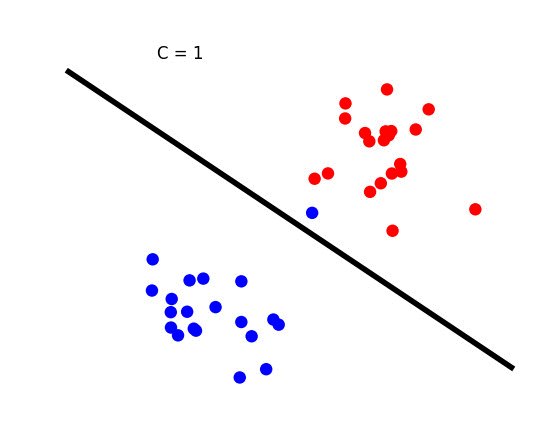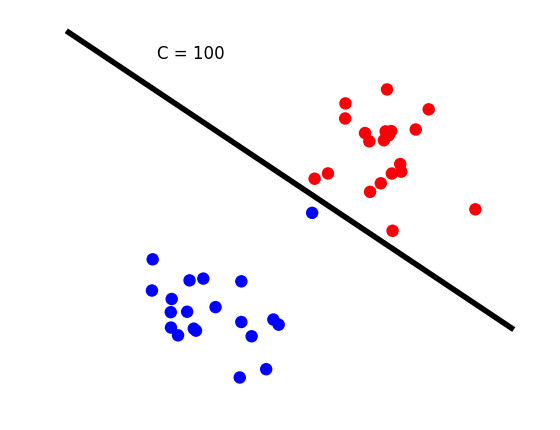
在下面的动画中，我们创建了这个场景。请注意，蓝点太靠近红色簇。选择默认值C = 1时，蓝点被错误分类。为C选择值100将其正确分类。

但是现在由黑线代表的决策边界太接近其中一个类。您是否愿意选择C为1，其中一个数据点被错误分类，但类之间的分离要好得多（减去一个数据点）？参数C允许您控制此权衡。

那么，你如何选择C？我们选择在提供的测试集上提供最佳分类的C. 该组中的图像未用于训练。

SVM参数Gamma：非线性SVM

你注意到了，我偷了几次“线性”这个词？在分类任务中，如果包含数据的空间可以使用平面（或2D中的线）进行分区以分隔类，则由多个类组成的数据集称为线性可分。

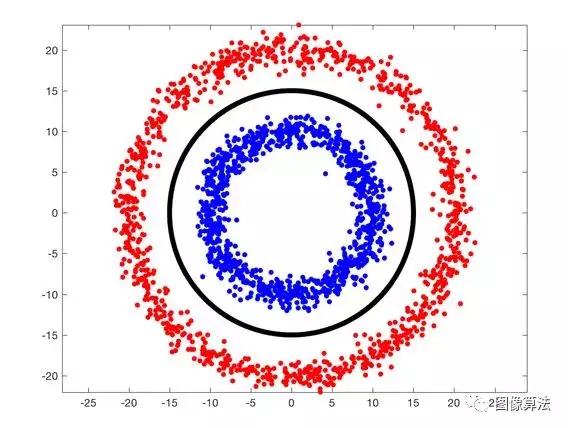
如果数据不是线性可分的怎么办？下图显示了使用红色和蓝色点的两个类，这些点不是线性可分的。您无法在平面上绘制一条线来分隔这两个类。使用黑线表示的良好分类器更像是一个圆圈。

在现实生活中，数据是混乱的，而不是线性可分的。

我们还可以使用SVM吗？答案是肯定的！

为此，您使用了一种称为Kernel Trick的技术。这是一个巧妙的技巧，可将非线性可分离数据转换为线性可分离数据。在我们的示例中，红色和蓝色点位于2D平面上。让我们使用以下等式为所有数据点添加第三维。

如果您听过人们使用带有高斯核的奇异项径向基函数（RBF），他们只是在谈论上面的等式。RBF只是一个实值函数，它仅取决于与原点的距离（即仅取决于）。的高斯核是指上式的高斯形式。更一般地，RBF可以具有不同种类的内核。你可以在这里看到其中一些。

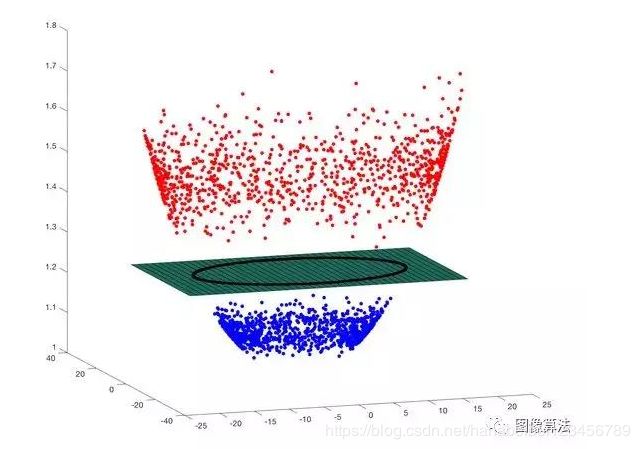
因此，我们根据其他两个维度中的数据制作了第三维。下图显示了这个三维（x，y，z）数据。我们可以看到它可以被包含黑色圆圈的平面分开！

 

参数Gamma（\伽玛）控制第三维中的数据拉伸。它有助于分类，但也会扭曲数据。像金发姑娘一样，你必须选择这个参数“恰到好处”。这是人们在训练SVM时选择的两个重要参数之一。

有了这些知识，我们现在准备使用OpenCV训练SVM。

使用OpenCV训练和测试SVM

在幕后，OpenCV使用LIBSVM。OpenCV 2.4.x中的SVM仍然使用C API。幸运的是，从3.x开始，OpenCV现在使用了更好的C ++ API。以下是在C ++和Python中使用OpenCV设置SVM的方法。

C++

// Set up SVM for OpenCV 3

Ptr svm = SVM::create();

// Set SVM type

svm->setType(SVM::C_SVC);

// Set SVM Kernel to Radial Basis Function (RBF)

svm->setKernel(SVM::RBF);

// Set parameter C

svm->setC(12.5);

// Set parameter Gamma

svm->setGamma(0.50625);

// Train SVM on training data

Ptr td = TrainData::create(trainData, ROW_SAMPLE, trainLabels);

svm->train(td);

// Save trained model

svm->save("digits_svm_model.yml");

// Test on a held out test set

svm->predict(testMat, testResponse);

Python

# Set up SVM for OpenCV 3

svm = cv2.ml.SVM_create()

# Set SVM type

svm.setType(cv2.ml.SVM_C_SVC)

# Set SVM Kernel to Radial Basis Function (RBF)

svm.setKernel(cv2.ml.SVM_RBF)

# Set parameter C

svm.setC(C)

# Set parameter Gamma

svm.setGamma(gamma)

# Train SVM on training data

svm.train(trainData, cv2.ml.ROW_SAMPLE, trainLabels)

# Save trained model

svm->save("digits_svm_model.yml");

# Test on a held out test set

testResponse = svm.predict(testData)[1].ravel()

自动训练SVM

可以想象，选择正确的SVM参数C和Gamma可能非常耗时。幸运的是，OpenCV 3.x C ++ API提供了一个功能，可以自动为您执行此超参数优化，并提供最佳的C和Gamma值。在上面的代码中，您可以将svm-> train（td）更改为以下内容

svm->trainAuto(td);

这种训练可能需要很长时间（比svm->训练多5倍），因为它基本上是多次训练。

OpenCV SVM错误

我们在使用OpenCV SVM时遇到了两个错误。第一个是确认的，但另外两个不是。

SVM模型不会在Python API中加载。如果您使用的是Python，您刚刚保存的训练有素的SVM模型将无法加载！错误修复会来吗？不！检查出来这里

trainAuto似乎没有通过Python API公开。

带有RBF内核的SVM在iOS / Android中不起作用。很高兴被证明是错误的，但在移动平台（iOS / Android）上，我们无法使用受RBF内核训练的SVM。SVM响应始终相同。线性SVM模型工作得很好。

结果

经过训练和一些超参数优化，我们在数字分类上达到了98.6％！不是，只需几秒钟的培训就不好了。

在训练集中的500个图像中，有7个被错误分类。图像及其错误分类的标签如下所示。就像父亲看着他孩子的错误一样，我想说的是这些错误是可以理解的。

源码地址关注微信公众号：“图像算法”或者微信搜索账号imalg_cn关注公众号 回复数字分类器