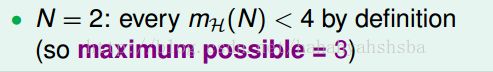机器学习基石-06-1-Restriction of Break Point
restrict of break point
四个成长函数的break point
那么break point到底有没有为我们未来到底能够产生几种dichotomy加上更强的限制呢?
首先理解一下break point k=2的意义:任意两个point不能shatter,不能shatter就是说不能出现完整的四种“OX”,"OO","XX","XO",如果在两个point上同时完成这四个,那就不满足break point的要求了。
break point k=2就等价于不能shatter!!一定要注意这个要求。
下面详细的解释一下k=2的几种情况:
1.k=2,当只有一个point点时(N=1),此时的成长函数一定可以shatter,也就是在某种点的组合上产生了两种dichotomy;
2.k=2,当存在两个point点时(N=2),不能shatter,因为break point=2,最多最多只有3个dichotomy,不可能实现“OX”,"OO","XX","XO"四种情况;
3.k=2,N=3时,最多可以产生多少种dichotomy呢?
第一种情况,产生了1种dichotomy,shatter any two points?------>NO
shatter any two points的含义:任意两个点是否满足shatter的条件,也就是四种情况“OX”,"OO","XX","XO"全都包含。
第二种情况,产生了2种dichotomy,shatter any two points?------>NO
第三种情况,产生了三个dichotomy:
第四种情况:产生了4个dichotomy,是否有两个点shatter?
可以明显地看到,上面的x2和x3在产生4种dichotomy的时候shatter了!“OX”,"OO","XX","XO"这四种情况都包含!此时就和break point k=2矛盾了,所以第四个dichotomy不能加进来!!!
那么重新进入另一个dichotomy呢?
此时的x2和x3不再shatter了,满足break point=2的要求。
第五种情况,产生了5个dichotomy,是否会有两个点shatter?
上面的x1和x3两个点shatter了,所以第五个dichotomy不能加进来!
那么再尝试加入另一个dichotomy呢?
可以看出,x1和x2两个点又shatter了!所以说明了最多只能产生4个dichotomy,加入第5个就一定会有两个点shatter,这个和break point的限制要求是矛盾的!
总结:
上面的例题,break point k=1的含义就是:任意一个点都不能shatter,也就是不能满足"O"和"X"两种情况。所以dichotomy只能有一个,因为加进来第二个dichotomy时,绝对会存在某一个点满足shatter,例如题目举例中的x3满足了shatter的条件。