(二)拉格朗日乘子法——KKT条件

假设目标函数是求解 f(x,y)=x2+y2 f ( x , y ) = x 2 + y 2 的最小问题。
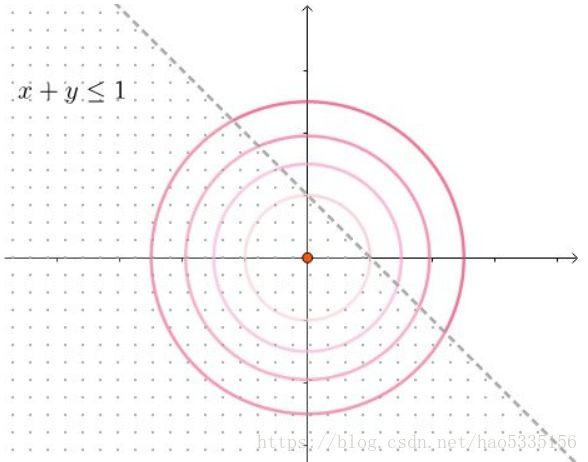
(1)假设约束条件是 h(x,y)=x+y⩽1 h ( x , y ) = x + y ⩽ 1 ，即

⎧⎩⎨⎪⎪minf(x,y)=x2+y2s.th(x,y)=x+y⩽1 { m i n f ( x , y ) = x 2 + y 2 s . t h ( x , y ) = x + y ⩽ 1

这个不等式约束实际上包含了原点，而原点是最小的值，所以这个约束条件等价于没有约束条件的求解，其求解过程是一样的

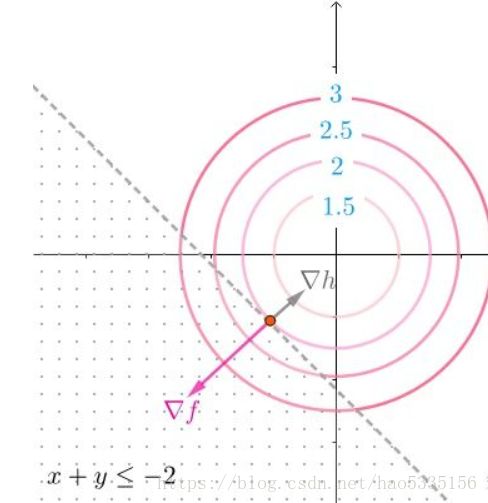
(2)假设约束条件是 h(x,y)=x+y⩽−2 h ( x , y ) = x + y ⩽ − 2 ，即

⎧⎩⎨⎪⎪minf(x,y)=x2+y2s.th(x,y)=x+y⩽−2 { m i n f ( x , y ) = x 2 + y 2 s . t h ( x , y ) = x + y ⩽ − 2

这个情况下，与约束条件是 g(x,y)=x+y=−2 g ( x , y ) = x + y = − 2 进行约束的求解过程是一样的

即求解

⎧⎩⎨⎪⎪▽f+μ▽h=0s.th(x,y)=x+y+2=0 { ▽ f + μ ▽ h = 0 s . t h ( x , y ) = x + y + 2 = 0

(3)新增的条件
不等式实际上带来了新的条件,因为梯度指向了函数增长的方向如图，所以目标函数的梯度如下图所示，而约束函数的梯度则是相反的方向(可以理解为对 h(x,y) h ( x , y ) 而言，对 x,y x , y 的偏导都需要使得 x,y x , y 变大，所以梯度为 ▽f ▽ f 的相反方向)(因为梯度下降法 w=w−α▽w w = w − α ▽ w 使得 w w 值变小)

所以，有

▽f+μ▽h=0,μ⩾0 ▽ f + μ ▽ h = 0 , μ ⩾ 0

其中， μ⩾0 μ ⩾ 0 表示 ▽f,▽h ▽ f , ▽ h 方向相反.
完整的方程组如下:

⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪▽f+μ▽h=0h(x,y)=x+y+2=0μ⩾0 { ▽ f + μ ▽ h = 0 h ( x , y ) = x + y + 2 = 0 μ ⩾ 0

综合以上，可以把求极值问题：

⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪minfs.tgi=0,i=1,2,...,nhi⩽0,i=1,2,...,m { m i n f s . t g i = 0 , i = 1 , 2 , . . . , n h i ⩽ 0 , i = 1 , 2 , . . . , m

通过解下面这个方程组来得到：

⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪▽f+∑niλi▽gi+∑mjμj▽hj=0gi=0,i=1,2,...,nhi⩽0,j=1,2,...,mμj⩾0μjhj=0 { ▽ f + ∑ i n λ i ▽ g i + ∑ j m μ j ▽ h j = 0 g i = 0 , i = 1 , 2 , . . . , n h i ⩽ 0 , j = 1 , 2 , . . . , m μ j ⩾ 0 μ j h j = 0

这个方程组也就是所谓的 KKT条件

参考非线性优化中的 KKT 条件该如何理解？