学会python可以做自己想做的事----用Python给你喜欢的音乐分个类吧

你喜欢什么样的音乐？目前，很多公司实现了对音乐的分类，要么是为了向客户提供推荐(如Spotify、SoundCloud)，要么只是作为一种产品(如Shazam)。对音乐进行分类，首先要确定音乐类型。事实证明，用机器学习技术从大量数据中找出音乐的各种潮流和类型是非常成功的。音乐分析亦然。

本文我们将学习如何用Python进行音频/音乐信号分析以及之后如何用该技能对不同类型的音乐片段进行分类。

在这里给大家推荐一个python系统学习q群：250933691有免费开发工具以及初学资料，（数据分析，爬虫，机器学习，神经网络）每天有老师给大家免费授课，欢迎一起交流学习

用Python处理音频

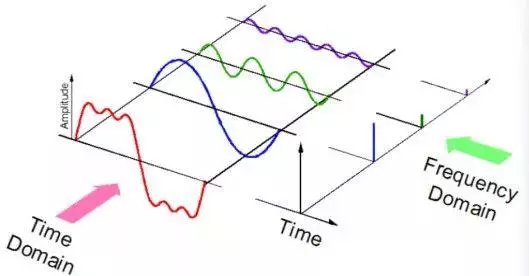
声音以音频信号的形式表示，音频信号具有频率、带宽、分贝等参数，音频信号一般可表示为振幅和时间的函数。

这些声音有多种格式，因此计算机可以对其进行读取和分析。例如：

• mp3 格式

• WMA (Windows Media Audio) 格式

• wav (Waveform Audio File) 格式

音频库

Python有一些很好用的音频处理库，比如Librosa和PyAudio。另外，还有一些基本的音频功能的内置模块。

我们将主要使用两个音频库进行音频采集和回放，如下：

1.Librosa

Librosa是一个Python模块，通常用于分析音频信号，但更适合音乐信号分析。它包括构建一个音乐信息检索（MIR）系统的具体细节，目前，Librosa已充分实现文档化，并具有许多相关的示例和教程。

安装

pip install librosa

or

conda install -c conda-forge librosa

可以安装附带很多音频解码器的ffmpeg（一个开源免费跨平台的视频和音频流方案）以提高音频解码功率。

2.IPython.display.Audio

IPython.display.Audio可以让用户直接在Jupyter notebook中播放音频。

音频包加载

import librosa

audio_path = '../T08-violin.wav'

x , sr = librosa.load(audio_path)

print(type(x), type(sr))

print(x.shape, sr)

(396688,) 22050

以上步骤的返回值为一段音频的时间序列，其默认采样频率(sr)为22KHZ mono。我们可将其改为：

librosa.load(audio_path, sr=44100)

可重新采样为44.1KHZ，

librosa.load(audio_path, sr=None)

或者不重新采样。

采样频率指音频每秒钟的采样样本数，以Hz或kHz表示。

音频播放

用Ipython.display.Audio 播放音频。

import IPython.display as ipd

ipd.Audio(audio_path)

 

以上步骤的返回值为Jupyter notebook的一个音频插件。如下：

这里的插件不起作用，不过放到你的notebooks上就可以了。

以下音频也可用mp3格式或WMA格式听。

可视化音频（Visualizing Audio）

波形音频 (Waveform)

我们可以用librosa.display.waveplot来绘制音频。

%matplotlib inline

import matplotlib.pyplot as plt

import librosa.display

plt.figure(figsize=(14, 5))

librosa.display.waveplot(x, sr=sr)

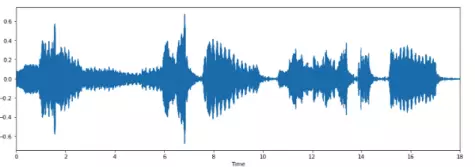
上图显示了该段波形音频的振幅包络线（amplitude envelope）。

声谱图（spectrogram）

声谱图（spectrogram）是声音或其他信号的频率随时间变化时的频谱（spectrum）的一种直观表示。声谱图有时也称sonographs,voiceprints,或者voicegrams。当数据以三维图形表示时，可称其为瀑布图（waterfalls）。在二维数组中，第一个轴是频率，第二个轴是时间。

我们可以用librosa.display.specshow 来展示声谱图。

X = librosa.stft(x)

Xdb = librosa.amplitude_to_db(abs(X))

plt.figure(figsize=(14, 5))

librosa.display.specshow(Xdb, sr=sr, x_axis='time', y_axis='hz')

plt.colorbar()

纵轴显示的是频率(从0到10kHz)，横轴显示的是音频的时间。因为所有可见的波动都发生在频谱的底部，故这里将频率轴转换成对数轴。

librosa.display.specshow(Xdb, sr=sr, x_axis='time', y_axis='log')

plt.colorbar()

音频编写

用librosa.output.write_wav 将NumPy数组保存到WAV文件中。

librosa.output.write_wav('example.wav', x, sr)

创建音频信号

现在让我们创建一个220HZ的音频信号。由于音频信号是一个numpy数组，所以创建后需将其转换为音频函数。

import numpy as np

sr = 22050 # sample rate

T = 5.0    # seconds

t = np.linspace(0, T, int(T*sr), endpoint=False) # time variable

x = 0.5*np.sin(2*np.pi*220*t)# pure sine wave at 220 Hz

Playing the audio

ipd.Audio(x, rate=sr) # load a NumPy array

Saving the audio

librosa.output.write_wav('tone_220.wav', x, sr)

然后，这就是你创建的第一个音频信号。

特征提取

每一个音频信号都有很多特征。然而，我们必须提取出与我们试图解决的问题相关的特征。提取特征以用于分析的过程称为特征提取。接下来我们将详细研究其中几个特征。

过零率（Zero Crossing Rate）

过零率（zero crossing rate）是一个信号符号变化的比率，即，在每帧中，语音信号从正变为负或从负变为正的次数。 这个特征已在语音识别和音乐信息检索领域得到广泛使用，通常对类似金属、摇滚等高冲击性的声音的具有更高的价值。

现在我们来计算示例音频片段的过零率：

# Load the signal

x, sr = librosa.load('../T08-violin.wav')

#Plot the signal:

plt.figure(figsize=(14, 5))

librosa.display.waveplot(x, sr=sr)

# Zooming in

n0 = 9000

n1 = 9100

plt.figure(figsize=(14, 5))

plt.plot(x[n0:n1])

plt.grid()

上图似乎有6个过零点，用librosa来验证下该结果。

zero_crossings = librosa.zero_crossings(x[n0:n1], pad=False)

print(sum(zero_crossings))

频谱质心（Spectral Centroid）

频谱质心指示声音的“质心”位于何处，并按照声音的频率的加权平均值来加以计算。 假设现有两首歌曲，一首是蓝调歌曲，另一首是金属歌曲。现在，与同等长度的蓝调歌曲相比，金属歌曲在接近尾声位置的频率更高。所以蓝调歌曲的频谱质心会在频谱偏中间的位置，而金属歌曲的频谱质心则靠近频谱末端。

用librosa.feature.spectral_centroid 计算出每一帧音频信号的频谱质心。

spectral_centroids = librosa.feature.spectral_centroid(x, sr=sr)[0]

spectral_centroids.shape

(775,)

# Computing the time variable for visualization

frames = range(len(spectral_centroids))

t = librosa.frames_to_time(frames)

# Normalising the spectral centroid for visualisation

def normalize(x, axis=0):

    return sklearn.preprocessing.minmax_scale(x, axis=axis)

#Plotting the Spectral Centroid along the waveform

librosa.display.waveplot(x, sr=sr, alpha=0.4)

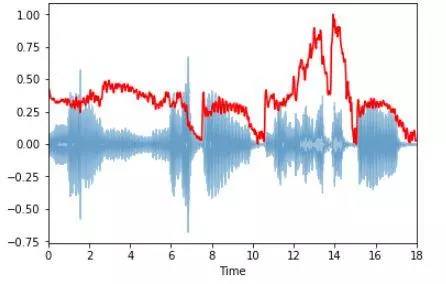
plt.plot(t, normalize(spectral_centroids), color='r')

频谱质心在接近末端处有上升。

谱滚降（Spectral Rolloff）

谱滚降（Spectral Rolloff）是对信号形状的测量，表示的是在谱能量的特定百分比(如85%)时的频率。

librosa.feature.spectral_rolloff 计算出每一帧信号的滚降频率。

spectral_rolloff = librosa.feature.spectral_rolloff(x+0.01, sr=sr)[0]

librosa.display.waveplot(x, sr=sr, alpha=0.4)

plt.plot(t, normalize(spectral_rolloff), color='r')

梅尔频率倒谱系数（Mel-Frequency Cepstral Coefficients）

信号的梅尔频率倒谱系数(MFCC)是一个通常由10-20个特征构成的集合，可简明地描述频谱包络的总体形状，对语音特征进行建模。

这次我们使用一个简单的循环波。

x, fs = librosa.load('../simple_loop.wav')

librosa.display.waveplot(x, sr=sr)

用librosa.feature.mfcc 计算出音频信号的梅尔频率倒谱系数：

mfccs = librosa.feature.mfcc(x, sr=fs)

print mfccs.shape

(20, 97)

#Displaying  the MFCCs:

librosa.display.specshow(mfccs, sr=sr, x_axis='time')

计算出该段超过97帧的音频的梅尔频率倒谱系数为20。

我们也可以给特征标上刻度，使其每个系数有相应的零均值和单位方差。

import sklearn

mfccs = sklearn.preprocessing.scale(mfccs, axis=1)

print(mfccs.mean(axis=1))

print(mfccs.var(axis=1))

librosa.display.specshow(mfccs, sr=sr, x_axis='time')

Chroma Frequencies

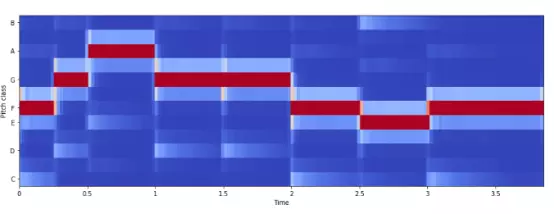
色度特征是对音乐音频的一种有趣生动的表示，可将整个频谱投射到代表“八度”（在音乐中，相邻的音组中相同音名的两个音，包括变化音级，称之为八度。）上12个不同的半音(或色度)的12进制上。色度向量（chroma vector ）(维基百科)(FMP，p.123)是一个通常包含12个元素特征的向量，表示信号中每个音级{C, C#, D, D#, E, …, B}中的能量。

用librosa.feature.chroma_stft 计算Chroma Frequencies。

# Loadign the file

x, sr = librosa.load('../simple_piano.wav')

hop_length = 512

chromagram = librosa.feature.chroma_stft(x, sr=sr, hop_length=hop_length)

plt.figure(figsize=(15, 5))

librosa.display.specshow(chromagram, x_axis='time', y_axis='chroma', hop_length=hop_length, cmap='coolwarm')

案例分析：对歌曲类型进行分类

以上我们对声学（听觉）信号及其特征和特征提取过程进行了概述，现在让我们用刚习得的技能来解决机器学习问题。

目标

本节，我们将尝试创建一个分类器将歌曲归为不同的类型。假设这样一个场景:出于某种原因，我们在硬盘上找到一堆随机命名的MP3文件，且文件里有音乐。我们的任务是根据音乐类型将它们分到不同的文件夹中，如爵士、古典音乐、乡村音乐、流行音乐、摇滚乐和金属乐。

数据集

我们将用最常用的的GITZAN数据集进行案例研究。G. Tzanetakis和P. Cook在2002年IEEETransactions on audio and Speech Processing中发表的著名论文： Musical genre classification of audio signals （音频信号的音乐类型分类）中曾用到该数据集。

该数据集每30秒包含1000条音轨，共包含10个音乐类型，即布鲁斯、古典、乡村、迪斯科、嘻哈、爵士、雷鬼、摇滚、金属和流行音乐。每种类型包含100段声频。

数据处理

在训练分类模型之前，我们须将原始数据从音频样本转换成更有意义的表示形式。需将音频片段从.au格式转换为能与python的 wave模块兼容的.wav格式，以读取音频文件。不过我常用的是开源SoX模块。

sox input.au output.wav

分类

特征提取（Feature Extraction）

我们接下来需要从音频文件中提取出有意义的特征。为了对音频片段进行分类，这里将选择5个特征，即梅尔频率倒谱系数(Mel-Frequency Cepstral Coefficients)，频谱质心 （Spectral Centroid），过零率（Zero Crossing Rate）， Chroma Frequencies，谱滚降（Spectral Roll-off）。然后将所有特征附加到.csv文件中，以便使用分类算法。

分类（Classification）

提取出特征后，用现有的分类算法将歌曲分为不同的类型。你可以直接用声谱图进行分类，也可以在提取特征后使用分类模型。

无论采用哪种方式，都要在模型上进行大量的实验。你可以进行试验和改进结果。建议试试CNN模型，它(在声谱图上)的精确度更高。

音乐类型分类的笔记

导入库

In [0]:

# feature extractoring and preprocessing data

import librosa

import pandas as pd

import numpy as np

import matplotlib.pyplot as plt

%matplotlib inline

import os

from PIL import Image

import pathlib

import csv

# Preprocessing

from sklearn.model_selection import train_test_split

from sklearn.preprocessing import LabelEncoder, StandardScaler

#Keras

import keras

import warnings

warnings.filterwarnings('ignore')

音乐和特征提取

数据集

我们用GTZAN genre collection 数据集进行分类。

数据集包含10中音乐类型。如下：

• 布鲁斯

• 古典

• 乡村

• 迪斯科

• 嘻哈

• 爵士

• 金属乐

• 流行音乐

• 雷鬼

• 摇滚

每一种音乐类型包含100首歌曲。共计1000首歌曲。

音频的声谱图提取

In [0]:

cmap = plt.get_cmap('inferno')

plt.figure(figsize=(10,10))

genres = 'blues classical country disco hiphop jazz metal pop reggae rock'.split()

for g in genres:

    pathlib.Path(f'img_data/{g}').mkdir(parents=True, exist_ok=True)     

    for filename in os.listdir(f'./MIR/genres/{g}'):

        songname = f'./MIR/genres/{g}/{filename}'

        y, sr = librosa.load(songname, mono=True, duration=5)

        plt.specgram(y, NFFT=2048, Fs=2, Fc=0, noverlap=128, cmap=cmap, sides='default', mode='default', scale='dB');

        plt.axis('off');

        plt.savefig(f'img_data/{g}/{filename[:-3].replace(".", "")}.png')

        plt.clf()

将所有的音频文件转换成相应的声谱图，以方便提取特征。

声谱图特征提取

我们将提取以下特征：

• 梅尔频率倒谱系数（Mel-frequency cepstral coefficients (MFCC)）(20 个)

• 频谱质心（Spectral Centroid）

• 过零率（Zero Crossing Rate）

• Chroma Frequencies

• 谱滚降（Spectral Roll-off）

In [0]:

header = 'filename chroma_stft rmse spectral_centroid spectral_bandwidth rolloff zero_crossing_rate'

for i in range(1, 21):

    header += f' mfcc{i}'

header += ' label'

header = header.split()

将数据写入csv 文件

In [0]:

file = open('data.csv', 'w', newline='')

with file:

    writer = csv.writer(file)

    writer.writerow(header)

genres = 'blues classical country disco hiphop jazz metal pop reggae rock'.split()

for g in genres:

    for filename in os.listdir(f'./MIR/genres/{g}'):

        songname = f'./MIR/genres/{g}/{filename}'

        y, sr = librosa.load(songname, mono=True, duration=30)

        chroma_stft = librosa.feature.chroma_stft(y=y, sr=sr)

        spec_cent = librosa.feature.spectral_centroid(y=y, sr=sr)

        spec_bw = librosa.feature.spectral_bandwidth(y=y, sr=sr)

        rolloff = librosa.feature.spectral_rolloff(y=y, sr=sr)

        zcr = librosa.feature.zero_crossing_rate(y)

        mfcc = librosa.feature.mfcc(y=y, sr=sr)

        to_append = f'{filename} {np.mean(chroma_stft)} {np.mean(rmse)} {np.mean(spec_cent)} {np.mean(spec_bw)} {np.mean(rolloff)} {np.mean(zcr)}'    

        for e in mfcc:

            to_append += f' {np.mean(e)}'

        to_append += f' {g}'

        file = open('data.csv', 'a', newline='')

        with file:

            writer = csv.writer(file)

            writer.writerow(to_append.split())

以上数据已被提取并写入data.csv文件。

用Pandas进行数据分析

In [6]:

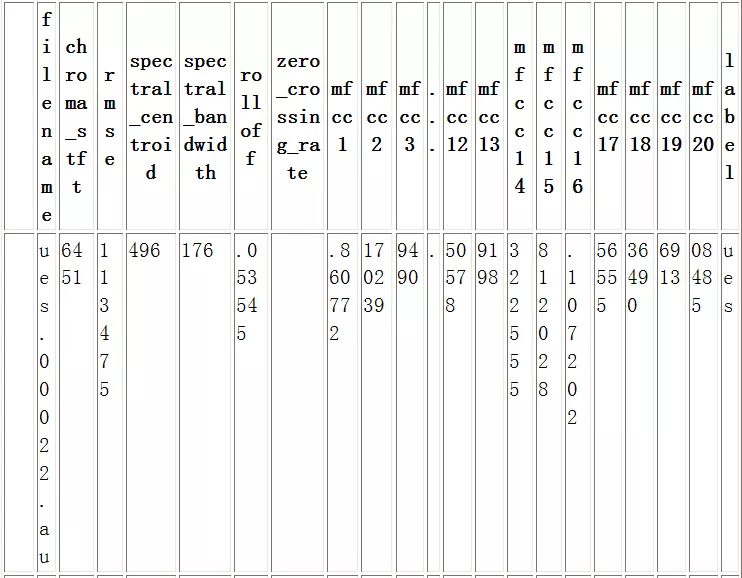
data = pd.read_csv('data.csv')

data.head()

Out[6]:

5行× 28列

In [7]:

data.shape

Out[7]:

(1000, 28)

In [0]:

# Dropping unneccesary columns

data = data.drop(['filename'],axis=1)

对标签进行编码

In [0]:

genre_list = data.iloc[:, -1]

encoder = LabelEncoder()

y = encoder.fit_transform(genre_list

给特征栏标上刻度

In [0]:

scaler = StandardScaler()

X = scaler.fit_transform(np.array(data.iloc[:, :-1], dtype = float))

将数据分为训练集和测试集

In [0]:

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

In [12]:

len(y_train)

Out[12]:

800

In [13]:

len(y_test)

Out[13]:

200

In [14]:

X_train[10]

Out[14]:

array([-0.9149113 ,  0.18294103, -1.10587131, -1.3875197 , -1.14640873,

       -0.97232926, -0.29174214,  1.20078936, -0.68458101, -0.55849017,

       -1.27056582, -0.88176926, -0.74844069, -0.40970382,  0.49685952,

       -1.12666045,  0.59501437, -0.39783853,  0.29327275, -0.72916871,

        0.63015786, -0.91149976,  0.7743942 , -0.64790051,  0.42229852,

       -1.01449461])

使用Keras进行分类 

创建自己的网络

In [0]:

from keras import models

from keras import layers

model = models.Sequential()

model.add(layers.Dense(256, activation='relu', input_shape=(X_train.shape[1],)))

model.add(layers.Dense(128, activation='relu'))

model.add(layers.Dense(64, activation='relu'))

model.add(layers.Dense(10, activation='softmax'))

In [0]:

model.compile(optimizer='adam',

              loss='sparse_categorical_crossentropy',

              metrics=['accuracy'])

In [19]:

history = model.fit(X_train,

                    y_train,

                    epochs=20,

                    batch_size=128)

Epoch 1/20

800/800 [==============================] - 1s 811us/step - loss: 2.1289 - acc: 0.2400

Epoch 2/20

800/800 [==============================] - 0s 39us/step - loss: 1.7940 - acc: 0.4088

Epoch 3/20

800/800 [==============================] - 0s 37us/step - loss: 1.5437 - acc: 0.4450

Epoch 4/20

800/800 [==============================] - 0s 38us/step - loss: 1.3584 - acc: 0.5413

Epoch 5/20

800/800 [==============================] - 0s 38us/step - loss: 1.2220 - acc: 0.5750

Epoch 6/20

800/800 [==============================] - 0s 41us/step - loss: 1.1187 - acc: 0.6288

Epoch 7/20

800/800 [==============================] - 0s 37us/step - loss: 1.0326 - acc: 0.6550

Epoch 8/20

800/800 [==============================] - 0s 44us/step - loss: 0.9631 - acc: 0.6713

Epoch 9/20

800/800 [==============================] - 0s 47us/step - loss: 0.9143 - acc: 0.6913

Epoch 10/20

800/800 [==============================] - 0s 37us/step - loss: 0.8630 - acc: 0.7125

Epoch 11/20

800/800 [==============================] - 0s 36us/step - loss: 0.8095 - acc: 0.7263

Epoch 12/20

800/800 [==============================] - 0s 37us/step - loss: 0.7728 - acc: 0.7700

Epoch 13/20

800/800 [==============================] - 0s 36us/step - loss: 0.7433 - acc: 0.7563

Epoch 14/20

800/800 [==============================] - 0s 45us/step - loss: 0.7066 - acc: 0.7825

Epoch 15/20

800/800 [==============================] - 0s 43us/step - loss: 0.6718 - acc: 0.7787

Epoch 16/20

800/800 [==============================] - 0s 36us/step - loss: 0.6601 - acc: 0.7913

Epoch 17/20

800/800 [==============================] - 0s 36us/step - loss: 0.6242 - acc: 0.7963

Epoch 18/20

800/800 [==============================] - 0s 44us/step - loss: 0.5994 - acc: 0.8038

Epoch 19/20

800/800 [==============================] - 0s 42us/step - loss: 0.5715 - acc: 0.8125

Epoch 20/20

800/800 [==============================] - 0s 39us/step - loss: 0.5437 - acc: 0.8250

In [20]:

test_loss, test_acc = model.evaluate(X_test,y_test)

200/200 [==============================] - 0s 244us/step

In [21]:

print('test_acc: ',test_acc)

test_acc:  0.68

以上数据的精确度不如训练数据的精确度高，这说明可能存在“过度拟合”（Overfitting）。

对所用方法进行验证

我们要从训练数据中留出200个样本作为测验集：

In [0]:

x_val = X_train[:200]

partial_x_train = X_train[200:]

y_val = y_train[:200]

partial_y_train = y_train[200:]

Now let's train our network for 20 epochs:

In [37]:

model = models.Sequential()

model.add(layers.Dense(512, activation='relu', input_shape=(X_train.shape[1],)))

model.add(layers.Dense(256, activation='relu'))

model.add(layers.Dense(128, activation='relu'))

model.add(layers.Dense(64, activation='relu'))

model.add(layers.Dense(10, activation='softmax'))

model.compile(optimizer='adam',

              loss='sparse_categorical_crossentropy',

              metrics=['accuracy'])

model.fit(partial_x_train,

          partial_y_train,

          epochs=30,

          batch_size=512,

          validation_data=(x_val, y_val))

results = model.evaluate(X_test, y_test)

Train on 600 samples, validate on 200 samples

Epoch 1/30

600/600 [==============================] - 1s 1ms/step - loss: 2.3074 - acc: 0.0950 - val_loss: 2.1857 - val_acc: 0.2850

Epoch 2/30

600/600 [==============================] - 0s 65us/step - loss: 2.1126 - acc: 0.3783 - val_loss: 2.0936 - val_acc: 0.2400

Epoch 3/30

600/600 [==============================] - 0s 59us/step - loss: 1.9535 - acc: 0.3633 - val_loss: 1.9966 - val_acc: 0.2600

Epoch 4/30

600/600 [==============================] - 0s 58us/step - loss: 1.8082 - acc: 0.3833 - val_loss: 1.8713 - val_acc: 0.3250

Epoch 5/30

600/600 [==============================] - 0s 59us/step - loss: 1.6663 - acc: 0.4083 - val_loss: 1.7302 - val_acc: 0.3450

Epoch 6/30

600/600 [==============================] - 0s 52us/step - loss: 1.5329 - acc: 0.4550 - val_loss: 1.6233 - val_acc: 0.3700

Epoch 7/30

600/600 [==============================] - 0s 62us/step - loss: 1.4236 - acc: 0.4850 - val_loss: 1.5402 - val_acc: 0.3950

Epoch 8/30

600/600 [==============================] - 0s 57us/step - loss: 1.3250 - acc: 0.5117 - val_loss: 1.4655 - val_acc: 0.3800

Epoch 9/30

600/600 [==============================] - 0s 52us/step - loss: 1.2338 - acc: 0.5633 - val_loss: 1.3927 - val_acc: 0.4650

Epoch 10/30

600/600 [==============================] - 0s 61us/step - loss: 1.1577 - acc: 0.5983 - val_loss: 1.3338 - val_acc: 0.5500

Epoch 11/30

600/600 [==============================] - 0s 64us/step - loss: 1.0981 - acc: 0.6317 - val_loss: 1.3111 - val_acc: 0.5550

Epoch 12/30

600/600 [==============================] - 0s 52us/step - loss: 1.0529 - acc: 0.6517 - val_loss: 1.2696 - val_acc: 0.5400

Epoch 13/30

600/600 [==============================] - 0s 52us/step - loss: 0.9994 - acc: 0.6567 - val_loss: 1.2480 - val_acc: 0.5400

Epoch 14/30

600/600 [==============================] - 0s 65us/step - loss: 0.9673 - acc: 0.6633 - val_loss: 1.2384 - val_acc: 0.5700

Epoch 15/30

600/600 [==============================] - 0s 58us/step - loss: 0.9286 - acc: 0.6633 - val_loss: 1.1953 - val_acc: 0.5800

Epoch 16/30

600/600 [==============================] - 0s 59us/step - loss: 0.8849 - acc: 0.6783 - val_loss: 1.2000 - val_acc: 0.5550

Epoch 17/30

600/600 [==============================] - 0s 61us/step - loss: 0.8621 - acc: 0.6850 - val_loss: 1.1743 - val_acc: 0.5850

Epoch 18/30

600/600 [==============================] - 0s 61us/step - loss: 0.8195 - acc: 0.7150 - val_loss: 1.1609 - val_acc: 0.5750

Epoch 19/30

600/600 [==============================] - 0s 62us/step - loss: 0.7976 - acc: 0.7283 - val_loss: 1.1238 - val_acc: 0.6150

Epoch 20/30

600/600 [==============================] - 0s 63us/step - loss: 0.7660 - acc: 0.7650 - val_loss: 1.1604 - val_acc: 0.5850

Epoch 21/30

600/600 [==============================] - 0s 65us/step - loss: 0.7465 - acc: 0.7650 - val_loss: 1.1888 - val_acc: 0.5700

Epoch 22/30

600/600 [==============================] - 0s 65us/step - loss: 0.7099 - acc: 0.7517 - val_loss: 1.1563 - val_acc: 0.6050

Epoch 23/30

600/600 [==============================] - 0s 68us/step - loss: 0.6857 - acc: 0.7683 - val_loss: 1.0900 - val_acc: 0.6200

Epoch 24/30

600/600 [==============================] - 0s 67us/step - loss: 0.6597 - acc: 0.7850 - val_loss: 1.0872 - val_acc: 0.6300

Epoch 25/30

600/600 [==============================] - 0s 67us/step - loss: 0.6377 - acc: 0.7967 - val_loss: 1.1148 - val_acc: 0.6200

Epoch 26/30

600/600 [==============================] - 0s 64us/step - loss: 0.6070 - acc: 0.8200 - val_loss: 1.1397 - val_acc: 0.6150

Epoch 27/30

600/600 [==============================] - 0s 66us/step - loss: 0.5991 - acc: 0.8167 - val_loss: 1.1255 - val_acc: 0.6300

Epoch 28/30

600/600 [==============================] - 0s 62us/step - loss: 0.5656 - acc: 0.8333 - val_loss: 1.0955 - val_acc: 0.6350

Epoch 29/30

600/600 [==============================] - 0s 66us/step - loss: 0.5513 - acc: 0.8300 - val_loss: 1.1030 - val_acc: 0.6050

Epoch 30/30

600/600 [==============================] - 0s 56us/step - loss: 0.5498 - acc: 0.8233 - val_loss: 1.0869 - val_acc: 0.6250

200/200 [==============================] - 0s 65us/step

In [38]:

results

Out[38]:

[1.2261371064186095, 0.65]

对测试集进行预测

In [0]:

predictions = model.predict(X_test)

In [26]:

predictions[0].shape

Out[26]:

(10,)

In [27]:

np.sum(predictions[0])

Out[27]:

1.0

In [28]:

np.argmax(predictions[0])

Out[28]:

8

In [0]:

下一步

音乐类型分类是音乐信息检索的众多分支之一。你还可以对音乐数据执行其他任务，如节拍跟踪（beat tracking）、音乐生成、推荐系统、音轨分离（track separation）、乐器识别等。音乐分析是一个既多元化又有趣的领域。音乐在某种程度上代表了用户的一个时刻。在数据科学领域，发现并描述这些时刻将会是一个有趣的挑战。

在这里给大家推荐一个python系统学习q群：250933691有免费开发工具以及初学资料，（数据分析，爬虫，机器学习，神经网络）每天有老师给大家免费授课，欢迎一起交流学习