机器学习之树回归（CART算法）

机器学习之树回归

• 1、分类树回归模型介绍
• 2、模型数学原理
• 3、算法及python实现
• 4、小结

1、分类回归树模型介绍

前面介绍了使用ID3算法进行决策树分类的模型，ID3算法的做法是每次选取当前最佳的特征来分割数据，并按照该特征的所有可能取值来切分，一旦按某种特征切分之后，该特征在之后的算法执行过程中将不再起作用，所以可以感觉到这种切分方法过于迅速，此外，ID3算法还存在一个问题，它不能直接处理连续型数据，只有事先将连续特征转换为离散型才能在ID3中起作用。
CART算法是十分著名且广泛记载的树构建算法，它使用二元切分来处理连续型变量，对CART算法稍作修改就能处理回归问题，回归树与分类树的思路类似，但叶结点的数据类型不是离散型二是连续型。

2、模型数学原理

1.最小二乘回归树生成算法
输入：训练数据集D;
输出：回归树f(x)
在训练集所在的输入空间中，递归地将每个区域划分为两个子区域并决定每个子区域上的输出值，构建二叉决策树；
（1）选择最优切分变量j与切分点s，求解

minj,s⎡⎣minc1∑xi∈R1(j,s)(yi−c1)2+minc2∑xi∈R2(j,s)(yi−c2)2⎤⎦ m i n j , s [ m i n c 1 ∑ x i ∈ R 1 ( j , s ) ( y i − c 1 ) 2 + m i n c 2 ∑ x i ∈ R 2 ( j , s ) ( y i − c 2 ) 2 ]

遍历变量j，对固定的切分变量j扫描切分点s，选择使上式达到最小值的（j,s）
（2）用选定的对(j,s)划分区域并决定相应的输出值：

R1(j,s)={x|x(j)≤s},R2(j,s)={x|x(j)>s} R 1 ( j , s ) = { x | x ( j ) ≤ s } , R 2 ( j , s ) = { x | x ( j ) > s }

cm^=1Nm∑xi∈Rm(j,s)yi,x∈Rm,m=1,2 c m ^ = 1 N m ∑ x i ∈ R m ( j , s ) y i , x ∈ R m , m = 1 , 2

（3）继续对两个子区域调用步骤（1），（2），直至满足停止条件为止
（4）将输入空间划分为M个区域 R1,R2,⋯,Rm R 1 , R 2 , ⋯ , R m ,生成决策树

f(x)=∑m=1Mcm^I(x∈Rm) f ( x ) = ∑ m = 1 M c m ^ I ( x ∈ R m )

2、CART分类树生成算法
输入：训练数据集D,停止计算条件；
输出：CART决策树；
根据训练集，从根节点开始，递归地对每个节点进行以下操作，构建二叉决策树：
（1）设结点的训练数据集为D，计算现有特征对该数据集的切分误差，此时，对于每一个特征A,对其可能取的每个值a，据此进行样本二分，计算两个子样本中标签项的方差之和。
（2）将所有可能得特征值A以及它们所有可能得切分点a中，选择样本划分之后方差和最小的值作为最优切分点，该值对应的特征为最优特征。依最优特征和最优切分点，从现结点生成两个子结点，将训练数据依特征分配到两个子结点中去。
（3）对两个子结点递归地调用（1），（2），直至满足停止条件
（4）生成CART决策树

3、算法及Python实现

CART算法是一个构建二叉树的算法，比较简单，具体算法参考上面：
Python实现
构建回归树和模型树

from numpy import *

def regLeaf(dataSet):
    return mean(dataSet[:,-1])
def regErr(dataSet):
    return var(dataSet[:,-1]) * shape(dataSet)[0]
def loadDataSet(fileName):
    dataMat = []
    fr = open(fileName)
    for line in fr.readlines():
        curLine = line.strip().split('\t')
        fltLine = list(map(float,curLine))
        dataMat.append(fltLine)
    return dataMat
def binSplitDataSet(dataSet,feature,value):
    mat0 = dataSet[nonzero(dataSet[:,feature] > value)[0],:]
    mat1 = dataSet[nonzero(dataSet[:,feature] <= value)[0],:]
    return mat0,mat1
def chooseBestSplit(dataSet,leafType=regLeaf,errType=regErr,ops=(1,4)):
    tolS = ops[0]; tolN = ops[1]
    if len(set(dataSet[:,-1].T.tolist()[0])) == 1:
        return None,leafType(dataSet)
    m,n = shape(dataSet)
    S = errType(dataSet)
    bestS = inf; bestIndex = 0; bestValue = 0
    for featIndex in range(n-1):
        for splitVal in set(dataSet[:,featIndex].T.tolist()[0]):
            mat0,mat1 = binSplitDataSet(dataSet,featIndex,splitVal)
            if(shape(mat0)[0] < tolN) or (shape(mat1)[0]continue
            newS = errType(mat0) + errType(mat1)
            if newS < bestS:
                bestIndex = featIndex
                bestValue = splitVal
                bestS = newS
        if(S-bestS) < tolS:
            return None,leafType(dataSet)
        mat0,mat1 = binSplitDataSet(dataSet,bestIndex,bestValue)
        if(shape(mat0)[0] < tolN) or (shape(mat1)[0] < tolN):
            return None,leafType(dataSet)
        return bestIndex,bestValue
def createTree(dataSet,leafType=regLeaf,errType=regErr,ops=(1,4)):
    feat,val = chooseBestSplit(dataSet,leafType,errType,ops)
    if feat == None:
        return val
    retTree = {}
    retTree['spInd'] = feat
    retTree['spVal'] = val
    lSet,rSet = binSplitDataSet(dataSet,feat,val)
    retTree['left'] = createTree(lSet,leafType,errType,ops)
    retTree['right'] = createTree(rSet,leafType,errType,ops)
    return retTree
def isTree(obj):
    return (type(obj).__name__ == 'dict')
def getMean(tree):
    if isTree(tree['right']):
        tree['right'] = getMean(tree['right'])
    if isTree(tree['left']):
        tree['left'] = getMean(tree['left'])
    return (tree['left']+tree['right'])/2.0
def prune(tree,testData): # CART 剪枝
    if shape(testData)[0] == 0:
        return getMean(tree)
    if(isTree(tree['right']) or isTree(tree['left'])):
        lSet,rSet = binSplitDataSet(testData,tree['spInd'],tree['spVal'])
    if isTree(tree['left']):
        tree['left'] = prune(tree['left'],lSet)
    if isTree(tree['right']):
        tree['right'] = prune(tree['right'],rSet)
    if not isTree(tree['left']) and not isTree(tree['right']):
        lSet,rSet = binSplitDataSet(testData,tree['spInd'],tree['spVal'])
        errorNoMerge = sum(power(lSet[:,-1]-tree['left'],2)) + sum(power(rSet[:-1]-tree['right'],2))
        treeMean = (tree['left']+tree['right'])/2.0
        errorMerge = sum(power(testData[:,-1]-treeMean,2))
        if errorMerge < errorNoMerge:
            print("merging")
            return treeMean
        else:
            return tree
    else:
        return tree

def linearSolve(dataSet): #模型树
    m,n = shape(dataSet)
    X = mat(ones((m,n)));Y = mat(ones((m,1)))
    X[:,1:n] = dataSet[:,0:n-1]; Y = dataSet[:,-1]
    xTx = X.T*X
    if linalg.det(xTx) == 0.0:
        raise NameError('This matrix is sigular,cannot do inverse\n')
    ws = xTx.I * (X.T * Y)
    return ws,X,Y
def modelLeaf(dataSet):
    ws,X,Y = linearSolve(dataSet)
    return ws
def modelErr(dataSet):
    ws,X,Y = linearSolve(dataSet)
    yHat = X * ws
    return sum(power(Y-yHat,2))

#用树回归进行预测
def regTreeEval(model,inDat):
    return float(model)
def modelTreeEval(model,inDat):
    n = shape(inDat)[1]
    X = mat(ones((1,n+1)))
    X[:,1:n+1]=inDat
    return float(X*model)
def treeForeCast(tree,inData,modelEval=regTreeEval):
    if not isTree(tree):
        return modelEval(tree,inData)
    if inData[tree['spInd']] > tree['spVal']:
        if isTree(tree['left']):
            return treeForeCast(tree['left'],inData,modelEval)
        else:
            return modelEval(tree['left'],inData)
    else:
        if isTree(tree['right']):
            return treeForeCast(tree['right'],inData,modelEval)
        else:
            return modelEval(tree['right'],inData)
def createForeCast(tree,testData,modelEval=regTreeEval):
    m = len(testData)
    yHat = mat(zeros((m,1)))
    for i in range(m):
        yHat[i,0] = treeForeCast(tree,mat(testData[i]),modelEval)
    return yHat

用tkinter创建可视化界面（所用到的数据集CART.rar）

from tkinter import *
from numpy import *
import matplotlib
matplotlib.use('TkAgg')
from matplotlib.backends.backend_tkagg import FigureCanvasTkAgg
from matplotlib.figure import Figure

def reDraw(tolS,tolN):
    reDraw.f.clf()
    reDraw.a = reDraw.f.add_subplot(111)
    if chkBtnVar.get():
        if tolN < 2:
            tolN = 2
        myTree = createTree(reDraw.rawDat,modelLeaf,modelErr,(tolS,tolN))
        yHat = createForeCast(myTree,reDraw.testDat,modelTreeEval)
    else:
        myTree = createTree(reDraw.rawDat,ops=(tolS,tolN))
        yHat = createForeCast(myTree,reDraw.testDat)
    reDraw.a.scatter(reDraw.rawDat[:,0].tolist(),reDraw.rawDat[:,1].tolist(),s=5)
    reDraw.a.plot(reDraw.testDat,yHat,linewidth=2.0)
    reDraw.canvas.show()
def getInputs():
    try:
        tolN = int(tolNentry.get())
    except:
        tolN = 10
        print("enter Integer for tolN")
        tolNentry.delete(0,END)
        tolNentry.insert(0,'10')
    try:
        tolS = float(tolSentry.get())
    except:
        tolS = 1.0
        print("enter Float for cols")
        tolSentry.delete(0,END)
        tolSentry.insert(0,'1.0')
    return tolN,tolS
def drawNewTree():
    tolN,tolS = getInputs()
    reDraw(tolS,tolN)

root = Tk()
# Label(root,text="Plot Place Holder").grid(row=0,columnspan=3)
reDraw.f = Figure(figsize=(5,4),dpi=100)
reDraw.canvas = FigureCanvasTkAgg(reDraw.f,master=root)
reDraw.canvas.show()
reDraw.canvas.get_tk_widget().grid(row=0,columnspan=3)
Label(root,text="tolN").grid(row=1,column=0)
tolNentry = Entry(root)
tolNentry.grid(row=1,column=1)
tolNentry.insert(0,'10')
Label(root,text="tolS").grid(row=2,column=0)
tolSentry = Entry(root)
tolSentry.grid(row=2,column=1)
tolSentry.insert(0,'1.0')
Button(root,text='ReDraw',command=drawNewTree).grid(row=1,column=2,rowspan=3)
chkBtnVar = IntVar()
chkBtn = Checkbutton(root,text="Model Tree",variable=chkBtnVar)
chkBtn.grid(row=3,column=0,columnspan=2)
reDraw.rawDat = mat(loadDataSet('./CART/sine.txt'))
reDraw.testDat = arange(min(reDraw.rawDat[:,0]),max(reDraw.rawDat[:,0]),0.01)
reDraw(1.0,10)
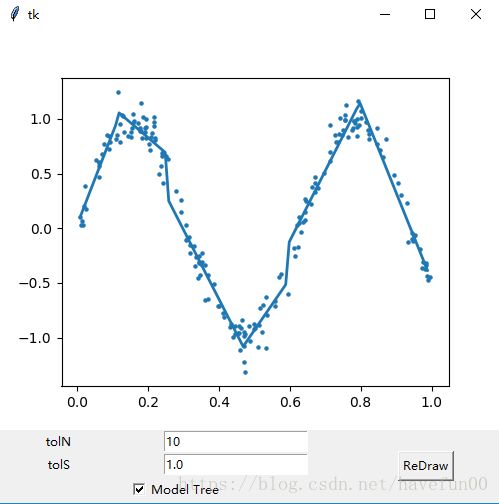
root.mainloop()

输出结果如图所示

4、小结

CART算法可以用于构建二元树并处理离散型或连续型数据的切分。若使用不同的误差预测准则就可以通过CART算法构建模型树和回归树。该算法构建出的树会倾向于对数据过拟合。因此需要进行剪枝操作，两种剪枝方法分别是预剪枝（在树进行构建过程中就剪枝）和后剪枝（当树构建完毕在进行剪枝），预剪枝更有效但需要用户定义一些参数。