深度学习—加快梯度下降收敛速度（一）：mini-batch、Stochastic gradient descent

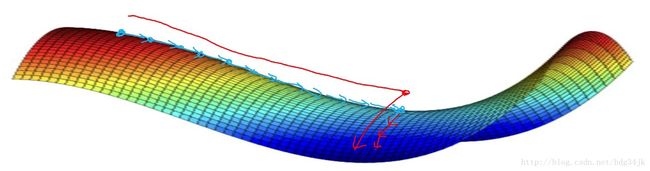
在深层神经网络那篇博客中讲了，深层神经网络的局部最优解问题，深层神经网络中存在局部极小点的可能性比较小，大部分是鞍点。因为鞍面上的梯度接近于0，在鞍面上行走是非常缓慢的。因此，必须想办法加速收敛速度，使其更快找到全局最优解。本文将介绍mini-batch与Stochastic gradient descent方法。

1.mini-batch

之前的梯度下降法是将训练集所有的梯度计算之后，再更新参数，这样大部分时间浪费在计算梯度上。而mini-batch是将训练集分组，分组之后，分别对每组求梯度，然后更新参数。加入分 8组，则每次迭代将会做8次梯度下降，更新8次参数。所以mini-batch比传统的梯度下降法下降的速度快，但是mini-batch的cost曲线没有传统梯度下降法的cost曲线光滑，大致对比如下：

梯度下降过程

mini-batch下降过程

mini-batch实现步骤：

• 确定mini-batch size，一般有32、64、128等，按自己的数据集而定，确定mini-batch_num=m/mini-batch_num + 1；
• 在分组之前将原数据集顺序打乱，随机打乱；
• 分组，将打乱后的数据集分组；
• 将分好后的mini-batch组放进迭代循环中，每次循环都做mini-batch_num次梯度下降。

2.Stochastic gradient descent

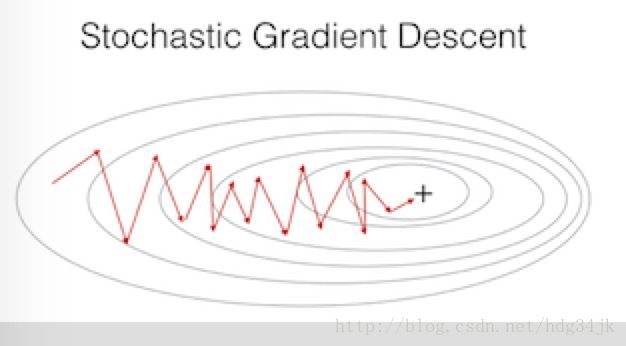
Stochastic gradient descent可以看做是mini-batch的一种特殊情况，当mini-batch size等于1时，mini-batch就退化为Stochastic gradient descent。此时每次迭代中，对于数据集中每个样本都做一次梯度下降，其梯度下降过程大致如下所示：

从Stochastic gradient descent的梯度下降图可以看出，下降速度虽然比传统梯度下降速度快，但是曲线比较曲折，没有mini-batch的曲线直，因此，多数情况下会使用mini-batch。

3.三者优缺点对比

• Stochastic gradient descent无法利用向量化，并行运算受限，mini-batch和batch gradient decent可以利用向量化，有并行运算优势；
• Stochastic gradient descent很难收敛到最优点，mini-batch和batch gradient decent可以收敛到最优点；
• Stochastic gradient descent和mini-batch收敛速度快，batch gradient decent收敛速度慢。

Stochastic gradient descent Python源码：

X = data_input
Y = labels
parameters = initialize_parameters(layers_dims)
for i in range(0, num_iterations):
    for j in range(0, m):
        # Forward propagation
        a, caches = forward_propagation(X[:,j], parameters)
        # Compute cost
        cost = compute_cost(a, Y[:,j])
        # Backward propagation
        grads = backward_propagation(a, caches, parameters)
        # Update parameters.
        parameters = update_parameters(parameters, grads)

mini-batch python 源码：

def random_mini_batches(X, Y, mini_batch_size = 64, seed = 0):
    """
    Creates a list of random minibatches from (X, Y)

    Arguments:
    X -- input data, of shape (input size, number of examples)
    Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (1, number of examples)
    mini_batch_size -- size of the mini-batches, integer

    Returns:
    mini_batches -- list of synchronous (mini_batch_X, mini_batch_Y)
    """

    np.random.seed(seed)            # To make your "random" minibatches the same as ours
    m = X.shape[1]                  # number of training examples
    mini_batches = []

    # Step 1: Shuffle (X, Y)
    permutation = list(np.random.permutation(m))
    shuffled_X = X[:, permutation]
    shuffled_Y = Y[:, permutation].reshape((1,m))

    # Step 2: Partition (shuffled_X, shuffled_Y). Minus the end case.
    num_complete_minibatches = int(math.floor(m/mini_batch_size)) # number of mini batches of size mini_batch_size in your partitionning
    for k in range(0, num_complete_minibatches):
        ### START CODE HERE ### (approx. 2 lines)
        mini_batch_X = shuffled_X[:, k * mini_batch_size:(k + 1) * mini_batch_size]
        mini_batch_Y = shuffled_Y[:, k * mini_batch_size:(k + 1) * mini_batch_size]
        ### END CODE HERE ###
        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.append(mini_batch)

    # Handling the end case (last mini-batch < mini_batch_size)
    if m % mini_batch_size != 0:
        ### START CODE HERE ### (approx. 2 lines)
        mini_batch_X = shuffled_X[:, (k + 1) * mini_batch_size:m]
        mini_batch_Y = shuffled_Y[:, (k + 1) * mini_batch_size:m]
        ### END CODE HERE ###
        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.append(mini_batch)

    return mini_batches