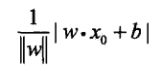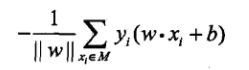统计学习-感知机算法

解决问题：二分类、线性分类（不能解决异或问题）

感知机（perceptron）：有监督学习、判别模型，SVM的基础

模型：

输入：

输出：

模型 参数为w和b

策略：

数据集满足线性可分性

学习一个能将正类和负类完全正确分开的分离超平面

1）依据误分类的点数（不是参数wb的连续可导函数，不易优化）

2）误分类点到超平面S的总距离

任意一点到超平面的距离：

（推导）替换为：

因此所有误分类点到超平面距离的和：

得出感知机学习的损失函数为：

学习算法：

随机梯度下降

1）

 2）对偶形式的区别是，引入了更新次数n

学习到的w和b有区别：

其中的yjxj已知，可以提前计算得出：Gram矩阵

简单形式代码：

import numpy as np
import matplotlib.pyplot as plt

class MyPerceptron:
    def __init__(self):
        self.w=None
        self.b=0
        self.l_rate=1

    def fit(self,X_train,y_train):
        #用样本点的特征数更新初始w，如x1=(3,3)T，有两个特征，则self.w=[0,0]
        self.w=np.zeros(X_train.shape[1])#列
        i=0
        while i

Sklearn实现：

from sklearn.linear_model import Perceptron
import numpy as np

X_train = np.array([[3, 3], [4, 3], [1, 1]])
y = np.array([1, 1, -1])

#perceptron=Perceptron()
perceptron=Perceptron(penalty="l2",alpha=0.01,eta0=1,tol=1e-3)
perceptron.fit(X_train,y)
print("w:",perceptron.coef_,"\n","b:",perceptron.intercept_,"\n","n_iter:",perceptron.n_iter_)

res=perceptron.score(X_train,y)
print("correct rate:{:.0%}".format(res))

X=X_train
X_new=np.array([[0], [6]])
w=perceptron.coef_
w=w.T
b=perceptron.intercept_
y_predict=(-b-(w[0]*X_new))/w[1]#W0x+w1y+b=0 则y=-b/w1-w0*x/w1
plt.plot(X[:2,0],X[:2,1],"g*",label="1")
plt.plot(X[2:,0], X[2:,1], "rx",label="-1")
#绘制分离超平面
plt.plot(X_new,y_predict,"b-")
#设置两坐标轴起止值
plt.axis([0,6,0,6]) 
#设置坐标轴标签  
plt.xlabel('x1')
plt.ylabel('x2')
#显示图例
plt.legend()
#显示图像
plt.show()
X1=np.array([[2,2]])
y2=perceptron.predict(X1)

函数： 

返回属性值

 

补充：

1）为什么不能解决异或问题？

  比如 00  （1） 11（1） 01（0） 10（0） 在坐标系中表示点，无法用一条直线将它们不同的类别完全划分开

参考资料

【1】统计机器学习

【2】中文文档https://sklearn.apachecn.org/

【3】https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Perceptron.html