序列模式PrefixSpan算法
序列模式PrefixSpan算法
https://wenku.baidu.com/view/ee189b72f46527d3240ce0f9.html
http://www.cnblogs.com/pinard/p/6323182.html
一、介绍
与GSP一样,PrefixSpan算法也是序列模式分析算法的一种,不过与GSP算法不同的是PrefixSpan算法不产生任何的侯选集,在这点上可以说已经比GSP好很多了。PrefixSpan算法可以挖掘出满足阈值的所有序列模式,可以说是非常经典的算法。
二、核心思想
PrefixSpan算法的全称是Prefix-Projected Pattern Growth,即前缀投影的模式挖掘。
核心思想:采用分治的思想,不断产生序列数据库的多个更小的投影数据库,然后在各个投影数据库上进行序列模式挖掘。它从长度为1的前缀开始挖掘序列模式,搜索对应的投影数据库得到长度为1的前缀对应的频繁序列,然后递归的挖掘长度为2的前缀所对应的频繁序列,……,以此类推,一直递归到不能挖掘到更长的前缀挖掘为止。
类似于树的深度优先搜索。
三、相关定义

1)ai=bi(i<=m-1)
2)bm Є am
3)所有在(bm-am)的连续项在bm中都是按照字母表顺序排列的
称b是a的一个前缀。

四、算法描述
输入:序列数据库S和支持度阈值α
输出:所有满足支持度要求的频繁序列集
1. 找出所有长度为1的前缀和对应的投影数据库
2. 对长度为1的前缀进行计数,将支持度低于阈值α的前缀对应的项从数据库S中删除,同时得到所有的频繁1项序列,i=1.
3. 对于每个长度为i满足支持度要求的前缀进行递归挖掘:
1) 找出前缀所对应的投影数据库。如果投影数据库为空,则递归返回。
2) 统计对应投影数据库中各项的支持度计数。如果所有项的支持度计数都低于阈值α,则递归返回。
3) 将满足支持度计数的各个单项和当前的前缀进行合并,得到若干新的前缀。
4) 令i=i+1,前缀为合并单项后的各个前缀,分别递归执行第3步。
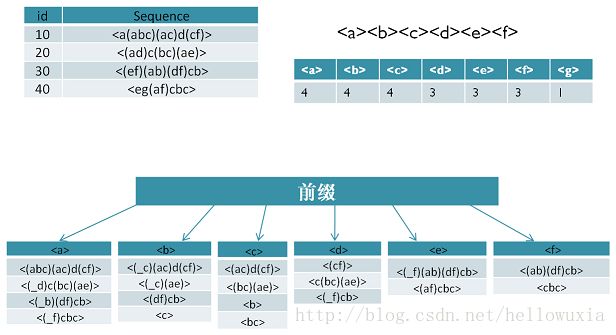
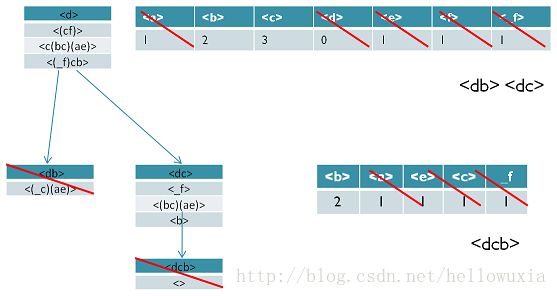
五、案例分析
如下例子,支持度阈值为50%。
六、算法效率分析
1.PrefixSpan算法不需要产生候选序列
与相似优先级算法不同,PrefixSpan算法从较短的连续项中产生序列模式增长很少在投影数据库中,不用生成候选序列,不用判断是否有候选序列的存在。
2.投影数据库一直缩小
投影数据库比原始数据库更小,因为只有那些有着连续前缀的后缀子序列才能投影到投影数据。因为:
1)通常在序列数据库中只有一组很小的序列模式增长的非常快,且当前缀增长时,投影数据库数量会变小;
2)投影仅仅发生在与前缀相关的后缀部分。
3.PrefixSpan算法主要消耗是构造投影数据库
在最坏情况下,PrefixSpan算法为每一个序列模式建立一个投影数据库。如果存在一些很大数量的序列模式,那么它的消耗是非平凡的。
为此,提出一个减小投影数据库个数的技术。
七、伪投影技术
1. 伪投影技术介绍
伪投影技术:能够减少投影数据库的数量和大小。
算法思想:当数据库可以存储在主存之中,我们就用一个指针指向数据库中的一个序列作为一个伪投影,而不是去通过收集所有的后缀而真实的构造物理投影。
每一个投影由两部分组成:指向数据库中序列的指针和序列中后缀的后继。
2.伪投影的分析
伪投影避免了物理的复制后缀,这样它在运行时间和空间上就很高效,但它不适用于基于硬盘的存取。因为随机存取硬盘空间是十分耗时的。
基于此原因,只要主存中可以容下一个投影数据库,就使用伪投影技术,如果原始序列数据库或投影数据库太大而不适应于主存,就用物理投影。
八、性能分析
PrefixSpan算法不论在运行时间还是空间上都大大优于SPADE、GSP算法,且与SPADE和GSP算法相比,在内存使用上更加稳定。
九、PrefixSpan算法高效的原因
1.不产生候选序列的模式增长
PrefixSpan算法是一个基于模式增长的算法,与基于优先级的传统算法不同,PrefixSpan算法没有产生任何没用序列,而且只是记下本地1-项组的频率。当最小支持度减小时,连续的序列就呈现指数增长,而基于最优化的算法会花费大量呈指数增长的时间去处理一个很小的数据库。
2.采用基于投影的分治法作为减小数据的有效方法
PrefixSpan算法的搜索空间是集中的且限制在一组投影数据库中。投影数据库的大小经常随挖掘进程的序列模式增长而快速减小。与之相比,基于优先级的算法经常在每次迭代过程中搜索原始的数据库。这样就会搜索和检查很多不相干的序列,增加负担。
3.PrefixSpan算法消耗相对稳定的内存
因为PrefixSpan算法不产生候选序列,且使用分治法进行搜索。另一方面,当支持度降到很小时,如GSP、SPADE算法,产生和检测候选序列的方法需要大量内存。
4.PrefixSpan算法应用于基于前缀的投影模式增长,比使用连续的模式定位投影方法FreeSpan算法更加高效。
与应用到FreeSpan算法中的前缀投影模式增长的连续投影相比,PrefixSpan算法仅在有后缀的连续项上进行投影,这样节省大量时间、空间,且投影的序列收缩很快。当挖掘很紧密的数据库时,FreeSpan算法不能从投影中获得很多,但PrefixSpan算法仍能在序列长度和投影数据库中序列个数上有很大减少。