吴恩达机器学习：线性回归

首先说一些关于课程的题外话。对于 Ng 的这个课程，笔者没有选择在 Coursera 上学习课程，一来是因为 Coursera 有自己的课程周期，但这个周期不一定适合所有人。其次 Coursera 的课程作业是使用 Octave 语言，而笔者个人觉得不管是学习还是未来使用 Python 都会是更合适的语言。所以最笔者选择了 课程视频 + Python 实现作业 的形式。

点击 课程视频 你就能不间断地学习 Ng 的课程，关于课程作业的 Python 代码已经放到了 Github 上，点击 课程代码 就能去 Github 查看（ 无法访问 Github 的话可以点击 Coding 查看 ），代码中的错误和改进欢迎大家指出。

以下是 Ng 机器学习课程第一周的笔记。

机器学习

什么是机器学习？Arthur Samuel 给出的一个非正式定义是：不通过明确地编程，使计算机拥有通过学习解决问题的能力。
机器学习的算法包括 监督学习，无监督学习，强化学习，推荐系统等。我们第一周学习的 线性回归 属于 监督学习。

回归问题

学习的目的是为了解决问题。回归问题是非常常见的一类问题，目的是为了找寻变量之间的关系。比如要从数据中找寻房屋面积与价格的关系，年龄与身高的关系，气体压力和体积的关系等等。而机器学习要做的正是要让机器自己来学习这些关系，并为对未知的情况做出预测。

监督学习的工作方式

首先要有一个训练数据集（ Training Set ），其中包含数据对应问题的正确结果。通过我们的学习算法 （ Learning Algorithm ） 学习训练数据集，最终获得一个函数 （ Hypothesis ），这个函数就是我们需要的 预测函数，能够对 训练集的数据 与 其它数据输入 做出比较准确的预测。

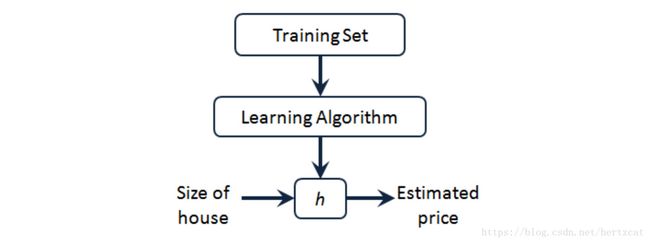
对于 线性回归 ，我们的 Hypothesis 就是：

hθ(x)=θ0+θ1x1+θ2x2+⋯+θnxn=θTx h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + ⋯ + θ n x n = θ T x

其中的 θi θ i 就是学习算法需要学习的参数，而 xi x i 是我们对于问题所选取的特征。

代价函数

那么如何学习 预测函数 中的 θi θ i 呢？我们需要引入 代价函数 的概念，它的作用是评估真实与预测值之间的差异。一旦有了这个函数，学习算法的目标就是找到 θi θ i 使得这个函数的值尽可能的小。对于 线性回归，我们使用的 代价函数 是：

J(θ)=12m∑i=1m(hθ(x(i))−y(i))2 J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2

其中 m m 是样本数， y y 是训练数据集已知答案，上标 i i 表示第几组训练数据， 代价函数 J(θ) J ( θ ) 是关于 θ θ 的函数。当然为了是表达更简洁、编写的程序更加清晰，我们通常会使用它的矩阵表达：

J(θ)=12m(Xθ−y)T(Xθ−y) J ( θ ) = 1 2 m ( X θ − y ) T ( X θ − y )

式中 X X 为所有训练特征数据组成的矩阵， y y 为训练数据集已知答案的列向量：

X=⎡⎣⎢⎢⎢⎢⎢11⋮1x(1)1x(2)1⋮x(m)1x(1)2x(2)2⋮x(m)2⋯⋯⋱⋯x(1)nx(2)n⋮x(m)n⎤⎦⎥⎥⎥⎥⎥      y=⎡⎣⎢⎢⎢⎢y(1)y(2)⋮y(m)⎤⎦⎥⎥⎥⎥ X = [ 1 x 1 ( 1 ) x 2 ( 1 ) ⋯ x n ( 1 ) 1 x 1 ( 2 ) x 2 ( 2 ) ⋯ x n ( 2 ) ⋮ ⋮ ⋮ ⋱ ⋮ 1 x 1 ( m ) x 2 ( m ) ⋯ x n ( m ) ]             y = [ y ( 1 ) y ( 2 ) ⋮ y ( m ) ]

最后为了承上启下，我们来看看当特征只有一个的时候， 代价函数 J(θ) J ( θ ) 的样子。

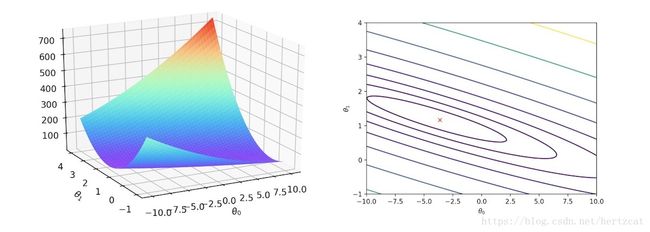
右图是 J(θ) J ( θ ) 的等高图，每一条线表示 代价函数 的值相同，红 X 表示 代价函数 的最低点。

梯度下降算法

接着刚刚看的单个特征所对应的 代价函数 图像加上之前所说的 “学习算法的目标就是找到 θi θ i 使得 代价函数 尽可能的小” 。一个很直观的想法就是，在坡上任意取一点，然后沿着下坡方向走最后到达最低点。这也正是梯度下降算法的思路，我们沿着梯度的反向更新 θi θ i 的值（ 沿着最陡的方向下坡 ），直到 代价函数 收敛到最小值。梯度下降算法更新 θi θ i 的方式为：

θi:=θi−α∂∂θiJ(θ) θ i := θ i − α ∂ ∂ θ i J ( θ )

其中 α α 为学习率， := := 表示使用右式的值替换 θi θ i 原有的值。对于 线性回归，我们更新 θi θ i 的方式为：

θ:=θ−α1mXT(Xθ−y) θ := θ − α 1 m X T ( X θ − y )

到这里我们就能够完成整个 线性回归 的机器学习算法了。设定 θi θ i 的初始值，使用梯度下降算法迭代更新 θi θ i 的值，直到 J(θ) J ( θ ) 收敛。至于为什使用梯度的反向可以看 这篇文章，作者从数学角度解释了原因。

正规方程

对于 线性回归，我们完全可以使用数学方法来得到 J(θ) J ( θ ) 取最小值时 θi θ i 的值。这涉及一些导数和线性代数的知识，有兴趣的同学可以详细看课程视频中的推导过程。这里直接给出求解 θ θ 的公式：

θ=(XTX)−1XTy θ = ( X T X ) − 1 X T y

在使用时 正规方程 有一定的限制，比如 XTX X T X 矩阵需要是可逆的。那么有了直接求解问题的方法，为什么我们还需要梯度下降的概念呢？因为梯度下降方法更具有广泛性，可以用于很多 问题的求解，比如非线性的 代价函数。

特征标准化

在实际的运用中我们选取的特征，比如长度，重量，面积等等，通常单位和范围都不同，这会导致梯度下降算法变慢。所以我们要将特征缩放到相对统一的范围内。通常的方法有 Standardization 和 Normalization。Standardization 是把数据变成符合标准正态分布，即使原来是些奇奇怪怪的分布，由 中心极限定理 可知，数据量够大，一样变成正态，更新公式为：

xi:=xi−μδ x i := x i − μ δ

Normalization 对于梯度下降算法友好，可能可以让算法最终收敛并且提高训练速度和精度，更新公式为：

xi:=xi−min(xi)max(xi)−min(xi) x i := x i − m i n ( x i ) m a x ( x i ) − m i n ( x i )

多项式回归

有时候线性的 Hypothesis 不一定合适我们需要拟合的数据，我们会选择多项式拟合例如：

hθ(x)=θ0+θ1x1+θ2x2+θ3x1x2+θ4x21+θ5x22 h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 1 x 2 + θ 4 x 1 2 + θ 5 x 2 2

这时候我们可以将它转化为 线性回归 问题，只要令新的特征 x3=x1x2 x 3 = x 1 x 2 ， x4=x21 x 4 = x 1 2 ， x5=x22 x 5 = x 2 2 就可以了。

So~，第一周的内容就是这些了，谢谢大家耐心阅读。