遗传算法(GA)的新手入门必备，python3案例

遗传算法简介

遗传算法（Genetic Algorithm）是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。遗传算法是从代表问题可能潜在的解集（即一个种群（population））开始的，而一个种群则由经过基因（gene）编码的一定数目的个体(individual)组成(可以把个体理解为一种可行解)。

每个个体实际上是染色体(chromosome)带有特征的实体。染色体作为遗传物质的主要载体，即多个基因的集合，其内部表现（即基因型）是某种基因组合，它决定了个体的形状的外部表现，如黑头发的特征是由染色体中控制这一特征的某种基因组合决定的。

---

大白话解释GA

简单来说，一开始是先随机取很多个可行解（构成一个种群），其中的每一个解（个体）都是由一条只含两种基因（0或1）的染色体（形如1001101101）组成，不同个体之间的染色体各不相同，但它们相互之间可以进行杂交（交换部分0101片段）、或者自己进行变异（比如某个0随机变成1）。

这个1001101101看上去似乎很抽象，其实如果按最简单的编码方式来理解，我们把它当成2进制数，则转化为十进制数就是621。比如在一个求解 maxf(x) m a x f ( x ) 的问题中，我们可以随机取50个十进制数（种群规模为50）转化（编码）成50个2进制数（这个二进制数其实就是一条染色体），然后在这批50个染色体中，找适度最好（即令 f(x) f ( x ) 比较大）的个体若干个，然后让这些能暂时取得比较大值的染色体去杂交或者发生变异。

我再说一下什么叫杂交变异，首先是变异，比如这里1001101101代表的621能使得 f(x) f ( x ) 取得不错的值，那么我们就认为最大值可能就在621附近，对其基因进行变异，使最后一位发生变化，即变成1001101100，这个数代表620，有可能取得一个更大的值。杂交和变异差不多，只不过杂交发生在两个基因之间，会同时改变两个染色体的基因片段。反正不管发生杂交或变异能不能取得更大，我们都会对种群中所有的基因进行新一轮的适度计算。但是也不是说杂交变异后的染色体都会需要，这时候需要进行选择，主要有轮赌法，即像转转盘抽奖一样，每个染色体都有个概率，中了就要，没中就白白。

经过上面的步骤，我们就有了一个新的种群，然后开始新的一轮计算。每一次计算都淘汰适度比较差的（即 f(x) f ( x ) 非常小，小于我们设定的某个阈值），然后幸存的个体才有权利进行杂交或者发生变异。周而复始，满足一定迭代次数或者一定阈值即可退出循环。

这里有一篇把遗传算法用袋鼠跳问题来形象比喻的，仍然不知道什么是GA的瞧一瞧
https://blog.csdn.net/u010451580/article/details/51178225

---

算法实现

参考：https://blog.csdn.net/czrzchao/article/details/52314455
这里我们用遗传算法来求解 y=10×sin(5x)+7×cos(4x) y = 10 × s i n ( 5 x ) + 7 × c o s ( 4 x ) 的最大值
首先看一下这个函数长什么样子

显然这么酷炫吊炸天的函数想直接求出最大值 ymax y m a x 似乎有点难。另外我们注意到这里横坐标可能带有小数点，似乎前面的二进制编码只能转成十进制的（即没有小数点），因此还需要用稍微改良的编码方式来对横坐标 x x 进行编码。

首先看看怎么把 x x 变成二进制形式，首先需要设定一定的码长 log2[(max−min)/精度+1] l o g 2 [ ( m a x − m i n ) / 精 度 + 1 ] ，这个精度的意思就是你想要这个实数有怎么样的精度，比如精确到0.01,0.0001?这就通过三个值来具体确定，就是 max m a x 、 min m i n 、精度。下面的代码实例中， max m a x 为变量upper_limit， min m i n 为0，精度为 210 2 10 ，其中10就是染色体长度。

解决了怎么把 x x 变成二进制，那如何把二进制变回 x x 呢，用下面这个公式：

x=min+二进制计算得到的十进制×(max−min)2染色体长度−1 x = m i n + 二 进 制 计 算 得 到 的 十 进 制 × ( m a x − m i n ) 2 染 色 体 长 度 − 1

大部分变量上面都提到过了，这里的二进制计算得到的十进制，就是最简单的进制转换了，比如一个二进制为10101，转化为十进制就是 1×24+0×23+1×22+0×21+1×20=21 1 × 2 4 + 0 × 2 3 + 1 × 2 2 + 0 × 2 1 + 1 × 2 0 = 21 ，再把21放到上面的解码公式就得到了最终的 x x 。

---

主要步骤

此次算法基本步骤：

随机产生种群pop
当迭代次数未到或还未找到满意解，进行如下循环：
1.检查每个染色体，计算适应性分数，评判染色体优劣。
2.从当前群体中选出2个成员。被选出的概率正比于染色体的适应性，适应性分数愈高，被选中的可能性也就愈大。常用的方法就是采用所谓的轮盘赌选择法或赌轮选择法(Roulette wheel selection)。
3.按照一定的交叉概率pc和交叉方法（crossover），生成新的个体。
4.按照一定的变异概率pm和变异方法（mutation），生成新的个体。
5.新一代种群产生，返回第1步。
结束循环

比如一开始随机产生了一个种群(包含很多 x x )，我们观摩一下一开始的情况：

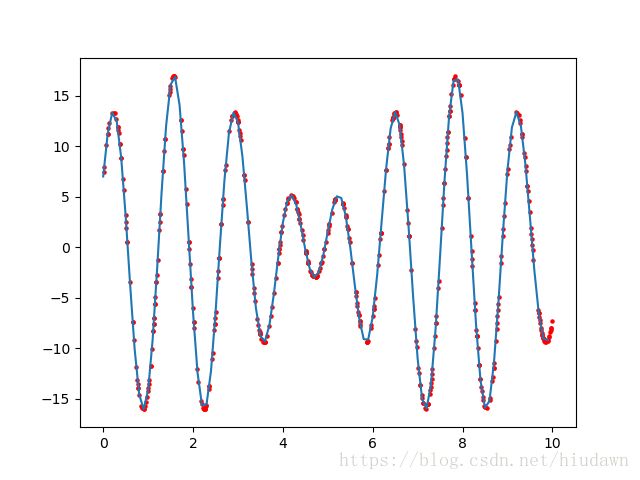
红点就是最初的一群 x x 和他们所取的值，我们要让他们往高处走，也就是要淘汰取值差的，经过一定迭代，得到：

即我们只让高处的活下来，值低的尽量都挂掉（但也不能全挂，不然很容易得到局部最优），这里是因为函数坐标可变范围较小，很容易就得到全局最优。

来看看各个迭代次数下 x x 对应的 y y 取值变化。

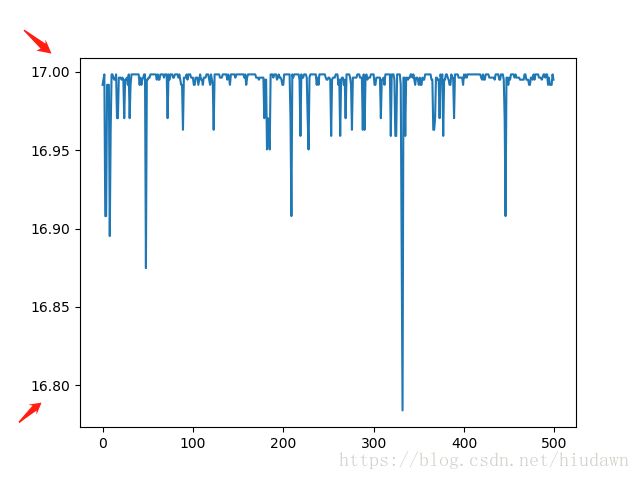
尽管这个图一直波动，但最终是在很接近17的位置。但波动永远不会停下来，因为这个算法本身就是启发式的，永远不会收敛。

---

代码示例

下面给出本次实验的代码

import matplotlib.pyplot as plt
import math
import random

"""
函数里面所有以plot开头的函数都可以注释掉，没有影响
求解的目标表达式为：
y = 10 * math.sin(5 * x) + 7 * math.cos(4 * x)
"""


def main():
    print('y = 10 * math.sin(5 * x) + 7 * math.cos(4 * x)')
    plot_obj_func()
    pop_size = 500  # 种群数量
    upper_limit = 10  # 基因中允许出现的最大值
    chromosome_length = 10  # 染色体长度
    iter = 500
    pc = 0.6 # 杂交概率
    pm = 0.01  # 变异概率
    results = []  # 存储每一代的最优解，N个二元组
    # pop = [[0, 1, 0, 1, 0, 1, 0, 1, 0, 1] for i in range(pop_size)]
    pop = init_population(pop_size, chromosome_length)
    best_X = []
    best_Y = []
    for i in range(iter):
        obj_value = calc_obj_value(pop, chromosome_length, upper_limit)  # 个体评价，有负值
        fit_value = calc_fit_value(obj_value)  # 个体适应度，不好的归0，可以理解为去掉上面的负值
        best_individual, best_fit = find_best(pop, fit_value)  # 第一个是最优基因序列, 第二个是对应的最佳个体适度
        # 下面这句就是存放每次迭代的最优x值是最佳y值
        results.append([binary2decimal(best_individual, upper_limit, chromosome_length), best_fit])

        # 查看一下种群分布
        # plot_currnt_individual(decode_chromosome(pop, chromosome_length, upper_limit), obj_value)

        selection(pop, fit_value)  # 选择
        crossover(pop, pc)  # 染色体交叉（最优个体之间进行0、1互换）
        mutation(pop, pm)  # 染色体变异（其实就是随机进行0、1取反）
        # 最优解的变化
        if iter % 20 == 0:
            best_X.append(results[-1][0])
            best_Y.append(results[-1][1])
    print("x = %f, y = %f" % (results[-1][0], results[-1][1]))
    # 看种群点的选择
    plt.scatter(best_X, best_Y, s=3, c='r')
    X1 = [i / float(10) for i in range(0, 100, 1)]
    Y1 = [10 * math.sin(5 * x) + 7 * math.cos(4 * x) for x in X1]
    plt.plot(X1, Y1)
    plt.show()
    # 看迭代曲线
    plot_iter_curve(iter, results)


# 看看我们要处理的目标函数
def plot_obj_func():
    """y = 10 * math.sin(5 * x) + 7 * math.cos(4 * x)"""
    X1 = [i / float(10) for i in range(0, 100, 1)]
    Y1 = [10 * math.sin(5 * x) + 7 * math.cos(4 * x) for x in X1]
    plt.plot(X1, Y1)
    plt.show()


# 看看当前种群个体的落点情况
def plot_currnt_individual(X, Y):
    X1 = [i / float(10) for i in range(0, 100, 1)]
    Y1 = [10 * math.sin(5 * x) + 7 * math.cos(4 * x) for x in X1]
    plt.plot(X1, Y1)
    plt.scatter(X, Y, c='r', s=5)
    plt.show()


# 看看最终的迭代变化曲线
def plot_iter_curve(iter, results):
    X = [i for i in range(iter)]
    Y = [results[i][1] for i in range(iter)]
    plt.plot(X, Y)
    plt.show()


# 计算2进制序列代表的数值
def binary2decimal(binary, upper_limit, chromosome_length):
    t = 0
    for j in range(len(binary)):
        t += binary[j] * 2 ** j
    t = t * upper_limit / (2 ** chromosome_length - 1)
    return t


def init_population(pop_size, chromosome_length):
    # 形如[[0,1,..0,1],[0,1,..0,1]...]
    pop = [[random.randint(0, 1) for i in range(chromosome_length)] for j in range(pop_size)]
    return pop


# 解码并计算值
def decode_chromosome(pop, chromosome_length, upper_limit):
    X = []
    for ele in pop:
        temp = 0
        # 二进制变成实数，种群中的每个个体对应一个数字
        for i, coff in enumerate(ele):
            # 就是把二进制转化为十进制的
            temp += coff * (2 ** i)

        # 这个是把前面得到的那个十进制的数，再次缩放为另一个实数
        # 注意这个实数范围更广泛，可以是小数了，而前面二进制解码后只能是十进制的数
        # 参考https://blog.csdn.net/robert_chen1988/article/details/79159244
        X.append(temp * upper_limit / (2 ** chromosome_length - 1))
    return X


def calc_obj_value(pop, chromosome_length, upper_limit):
    obj_value = []
    X = decode_chromosome(pop, chromosome_length, upper_limit)
    for x in X:
        # 把缩放过后的那个数，带入我们要求的公式中
        # 种群中个体有几个，就有几个这种“缩放过后的数”
        obj_value.append(10 * math.sin(5 * x) + 7 * math.cos(4 * x))
    # 这里先返回带入公式计算后的数值列表，作为种群个体优劣的评价
    return obj_value


# 淘汰
def calc_fit_value(obj_value):
    fit_value = []
    # 去掉小于0的值，更改c_min会改变淘汰的下限
    # 比如设成10可以加快收敛
    # 但是如果设置过大，有可能影响了全局最优的搜索
    c_min = 10
    for value in obj_value:
        if value > c_min:
            temp = value
        else:
            temp = 0.
        fit_value.append(temp)
    # fit_value保存的是活下来的值
    return fit_value


# 找出最优解和最优解的基因编码
def find_best(pop, fit_value):
    # 用来存最优基因编码
    best_individual = []
    # 先假设第一个基因的适应度最好
    best_fit = fit_value[0]
    for i in range(1, len(pop)):
        if (fit_value[i] > best_fit):
            best_fit = fit_value[i]
            best_individual = pop[i]
    # best_fit是值
    # best_individual是基因序列
    return best_individual, best_fit


# 计算累计概率
def cum_sum(fit_value):
    # 输入[1, 2, 3, 4, 5]，返回[1,3,6,10,15]，matlab的一个函数
    # 这个地方遇坑，局部变量如果赋值给引用变量，在函数周期结束后，引用变量也将失去这个值
    temp = fit_value[:]
    for i in range(len(temp)):
        fit_value[i] = (sum(temp[:i + 1]))


# 轮赌法选择
def selection(pop, fit_value):
    # https://blog.csdn.net/pymqq/article/details/51375522

    p_fit_value = []
    # 适应度总和
    total_fit = sum(fit_value)
    # 归一化，使概率总和为1
    for i in range(len(fit_value)):
        p_fit_value.append(fit_value[i] / total_fit)
    # 概率求和排序

    # https://www.cnblogs.com/LoganChen/p/7509702.html
    cum_sum(p_fit_value)
    pop_len = len(pop)
    # 类似搞一个转盘吧下面这个的意思
    ms = sorted([random.random() for i in range(pop_len)])
    fitin = 0
    newin = 0
    newpop = pop[:]
    # 转轮盘选择法
    while newin < pop_len:
        # 如果这个概率大于随机出来的那个概率，就选这个
        if (ms[newin] < p_fit_value[fitin]):
            newpop[newin] = pop[fitin]
            newin = newin + 1
        else:
            fitin = fitin + 1
    # 这里注意一下，因为random.random()不会大于1，所以保证这里的newpop规格会和以前的一样
    # 而且这个pop里面会有不少重复的个体，保证种群数量一样

    # 之前是看另一个人的程序，感觉他这里有点bug，要适当修改
    pop = newpop[:]


# 杂交
def crossover(pop, pc):
    # 一定概率杂交，主要是杂交种群种相邻的两个个体
    pop_len = len(pop)
    for i in range(pop_len - 1):
        # 随机看看达到杂交概率没
        if (random.random() < pc):
            # 随机选取杂交点，然后交换数组
            cpoint = random.randint(0, len(pop[0]))
            temp1 = []
            temp2 = []
            temp1.extend(pop[i][0:cpoint])
            temp1.extend(pop[i + 1][cpoint:len(pop[i])])
            temp2.extend(pop[i + 1][0:cpoint])
            temp2.extend(pop[i][cpoint:len(pop[i])])
            pop[i] = temp1[:]
            pop[i + 1] = temp2[:]


# 基因突变
def mutation(pop, pm):
    px = len(pop)
    py = len(pop[0])
    # 每条染色体随便选一个杂交
    for i in range(px):
        if (random.random() < pm):
            mpoint = random.randint(0, py - 1)
            if (pop[i][mpoint] == 1):
                pop[i][mpoint] = 0
            else:
                pop[i][mpoint] = 1


if __name__ == '__main__':
    main()

---

后话

其实这个算法的入门非常不难，难就在于怎么应用于各种实际问题，这次看到遗传算法这个名字就有点怕，果然没什么好怕的。希望能继续加油，学会更多。