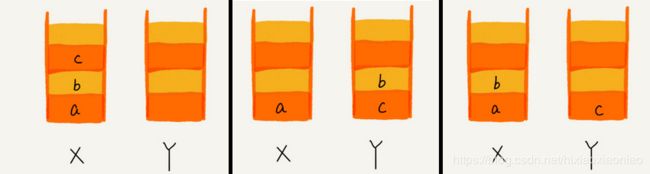数据结构与算法--线性数据结构

目录

数组

链表

栈

队列

跳表

散列表

散列表+链表

参考

---

 

数组

数组是一种线性表数据结构，它用一组连续的内存空间，来存储一组具有相同类型的数据
数组，链表，队列，栈都是线性表结构
非线性表结构有 树，二叉树，堆，图等

数组下标从0开始，确切定义是偏移offset，用a来表示数组首位地址，a[0]就是偏移为0的位置
a[k]表示k个type_size 位置，计算a[k]内存地址的公式

a[k]_address = hbase_address + k * type_size

如果下标从1开始，则计算a[k]内存地址就变为

a[k]_address = hbase_address + (k-1)*type_size

数组的 O(1)插入
如果数组不要求有序，假设插入到第k个位置，可以先将第k位的元素移到数组最后，
再将新元素插入到第k位
假设数组中有a，b，c，d，e几个元素，将x插入到第三个位置，只需要将c移到a[5]，结果就是
a，b，x，d，e，c

如果删除时不要求数据一定连续，可以将多次的删除操作合并到一起执行，提高效率
这就是JVM标记清除垃圾算法的核心

一段死循环代码

#include 
#include 
#include 
int main(int argc, char *argv[]) {
    int i = 0;
    int arr[3] = {0};
    for(;i<=3;i++) {
        arr[i] = 0;
        printf("hello world\n");
    }
    return 0;
}

栈是从高到低增长的，所以栈中的元素顺序是i,a[2],a[1],a[0]对如下代码

int i = 0;
int j = 1;
int k = 2;
int arr[3] = {0}; 
cout<<"i-"<<&i<

 

 

 

链表

• 单链表
• 循环单链表(约瑟夫环问题)
• 双链表
• 双向循环链表

几个写链表的技巧

• 理解指针或引用的含义
• 警惕指针丢失和内存泄露
• 利用哨兵建好实现难度
• 重点留意边界条件处理
• 举例画图辅助思考

5个常见的链表操作

• 单链表反转
• 链表中的循环检测
• 两个有序的链表合并
• 删除链表倒数第n个节点
• 求链表的中间节点

其他
一个字符串中是否有回文字符串
单链表存储的字符串，如何判断回文

 

栈

• 顺序栈
• 链式栈
• 支持动态扩容的顺序栈

根据均摊分析动态扩容的顺序栈时间复杂度是O(1)
栈的实际应用

• 函数调用栈
• 表达式求值
• 括号匹配中的应用

模拟浏览器前进后退功能

• 使用两个栈X，Y
• 首次浏览的页面压入X栈
• 点击后退时，依次从X栈弹出放到Y栈中
• 通过页面b又跳转到新页面d，页面C就无法通过前进后退按钮重复查看了，要清空栈Y

 

 

队列

也是一种操作受限的线性表数据结构

• 顺序队列
• 链式队列
• 循环队列
• 阻塞队列
• 并发队列

顺序队列当tail指针移动到数组最右边后，如有新数据入队，可以将head到tail之间的数据
整体搬移到数组中0到tail-head的位置
循环队列实现的关键，确定好队空和队满的条件

 

 

跳表

对链表的改造，可以支持二分查找的链表
可以替代红黑树的动态数据结构
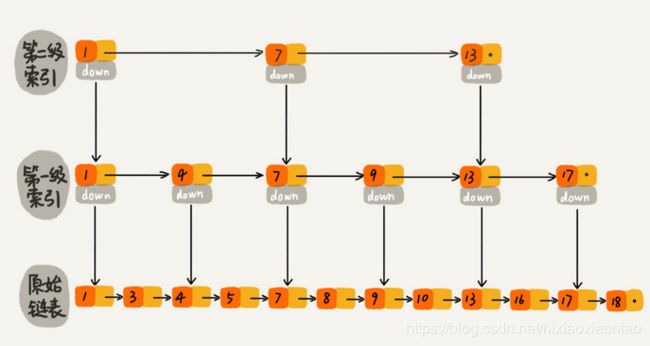
在原始的节点之上，增加了一层，两层，多层的索引，提高搜索效率

下图是一个64个节点的链表，有5层索引，如果搜索62个节点需要遍历62次，现在只需要11次

这种链表加多级索引的结构，就是跳表
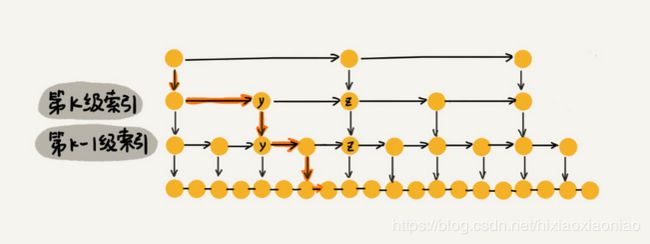
假设第一级索引是n/2，第二级是n/4，第k级索引节点是n/(2^k)
假设每一层要遍历m次，跳表的时间复杂度是O(m*logn)
可以算出每一层只需要遍历三次，也就是m=3，所以时间复杂度是O(logn)

跳表的空间复杂度为O(n)

如果每3个或者5个节点，抽一个节点到上级索引，其空间复杂度大概能降低一半

实际开发中，链表中的数据可能很大，索引节点存储的只是指针，所以空间可以忽略

跳表中删除/插入操作，需要先找到这个节点/或者前驱节点，再执行操作
找到某个节点的操作时间是O(logn)，插入和删除的操作时间是O(1)，所以总的时间就是O(logn)
如果不停的往跳表中插入数据，不更新索引，可能出现2个索引节点直接数据非常多，极端情况下就退化成了单链表

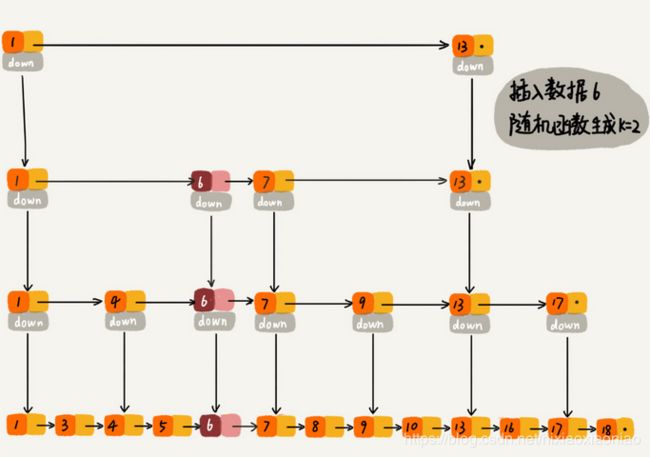
类似AVL树和红黑树的左右旋转操作，跳表是通过一个随机函数，来决定这个节点插入到哪几级索引中
如果随机函数生产了值K，就将这个节点添加到第一级到第K级索引中

这里的随机函数选择就很有讲究了，需要从概率上保证跳表索引大小和数据大小平衡，不至于性能过度退化
Redis中的有序集合是通过跳表来实现的(还用到了散列表)：

1. 插入一个数据
2. 删除一个数据
3. 查找一个数据
4. 按区间查找数据(如查到[100，356]之间的数据)
5. 迭代输出有序数据

红黑树可以完成1，2，3，5但是第4点就不行了
跳表可以用O(logn)时间定位到一个指定的值如100，然后遍历这个链表后续的值就可以了

 

 

散列表

1. 散列函数的设计，不能太复杂，生成的值要随机均匀
2. 装载因子过大后支持动态扩容(小于某个阈值可以缩容)
3. 散列冲突，开放寻址 和 链表

开放寻址vs链表

• 数据量小时可以采用开放寻址法，Java的ThreadLocalMap使用了，同一个数组中利用cpu缓存
• 链表法适合存储大对象，大数据量，当链>8启动红黑树，当链<8退回为链表

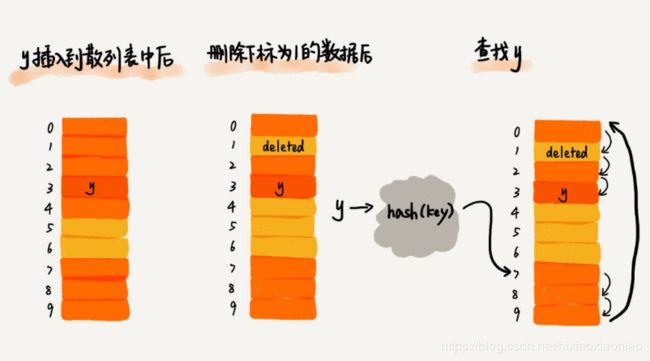
开放地址法
包括普通的线性探测
二次探测
双重散列
当删除一个元素时，不能直接删除，否则线性探测发现这个位置为空就会判断失败，得加上deleted标志

Java的HashMap散列函数

int hash(Object key) {
    int h = key.hashCode();
    //这里使用了异或，和位移，计算出来的具有高低位性质，同时用 & 模拟取余运行达到均匀分布
    return (h ^ (h >>> 16)) & （capitity -1）;
}

 避免低效扩容
如果散列表已经有1G了，此时空间不够再扩容一倍变成2G，而且所有的key都需要重新计算散列函数
可以先申请2G的空间，但不做搬移操作，新的key插入到新的散列表中，再从老表中拿一个key重新计算后放入新表
查询时为了兼容老的，需要先从新的中查询如果没有再去老的中查询
这样的均摊方法，将一次性扩容的代价，均摊到多次插入操作中

 

散列表+链表

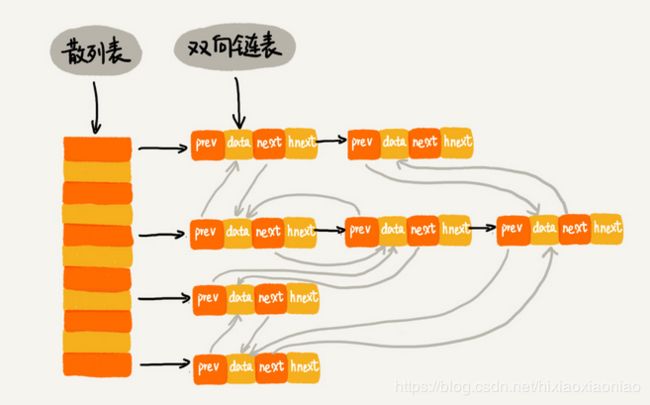
LRU缓存淘汰机制，需要用到散列表+链表的方式，结构如下

链表中的数据节点data，还有前驱节点prev，后驱节点next，新增了一个特殊节点hnext
前驱和后驱针织是为了将节点串在双向链表中
hnext指针是为了将节点串在散列表的拉链中
按照这个图的原理，查找，删除，增加都是O(1)时间复杂度

Redis有序集合中，有两个重要属性key键值 score分值
可以通过用户ID来查找积分信息，也可以通过积分区间来查找用户ID或者姓名
Redis有序集合包括如下操作

• 添加一个成员对象
• 按照键值来删除一个成员对象
• 按照键值来查找一个成员对象
• 按照分值区间查找数据，如查找积分在[100，356]之间的成员对象
• 按照分值从小到大排序成员变量

以上需求如果只是用跳表就不行了，需要用链表+散列表的方式才可以

Java的LinkedHashMap 也是类似的散列表+链表的实现方式
底层就是HashMap，又加了一个双向链表，通过双向链表维持插入顺序
LinedHashMap也支持按访问顺序来操作元素，当一个元素被访问时，就将其放到链表末尾，但散列表中的位置不动

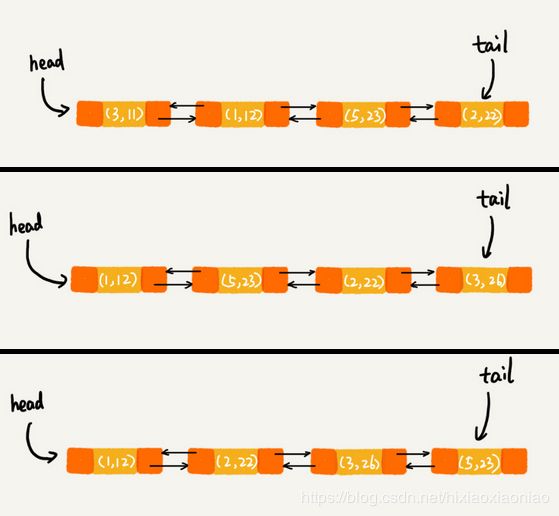
下面是操作Java的LinkedHashMap的三个操作

• 第一次将4个元素put到map中，链表的结构如下
• 第二次修改key为3的值，于是将key为3的元素放到链表末尾
• 第三次访问key为5的元素，于是将key为5的元素放到链表末尾

 

 

 

 

 

参考

跳表的实现

Redis源码学习跳表

图解LinkedHashMap原理