2线性分类器基本原理-2.3线性分类器之SoftMax和交叉熵损失(Cross-Entropy)

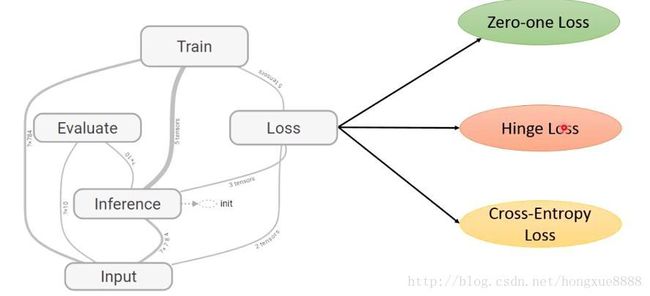
图像分类器模型的整体结构：

交叉熵（Cross-Entropy）损失 和 SoftMax
SVM是最常用的两个分类器之一，而另一个就是Softmax分类器，它的损失函数与SVM损失函数不同。对于学习过二元逻辑回归分类器的读者来说，SoftMax分类器就可以理解为逻辑回归分类器面对多个分类的一般化归纳。SVM将输出 f(xi,W) 作为每个分类的评分（因为无定标，所以难以直接解释）。与SVM不同，Softmax的输出（归一化的分类概率）更加直观，并且从概率上可以解释，这一点后文会讨论。在Softmax分类器中，函数映射 f(xi,W)=Wxi 保持不变，但将这些评分值视为每个分类的未归一化的对数概率，并且将折叶损失（hinge loss）替换为交叉熵损失（cross-entropy loss）。公式如下：

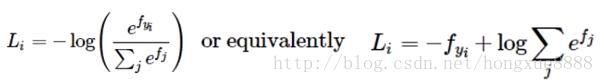
在上式中，使用 fj 来表示分类评分向量f中的第j个元素。和之前一样，整个数据集的损失值是数据集中所有样本数据的损失值 Li 的均值与正则化损失 R(W) 之和

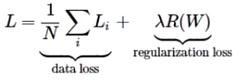
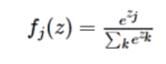
（参考：https://en.wikipedia.org/wiki/Softmax_function）
被称为softmax函数：其输入值是一个向量，向量中元素为任意实数的评分值（z中的），函数对其进行压缩，输出一个向量，其中每个元素值在0到1之间，且所有元素之和为1。所以，包含softmax函数的完整交叉熵损失看起来唬人，实际上还是比较容易理解的。

信息理论视角：在“真实”分布p和估计分布q之间的交叉熵定义如下：

。。。

---

让人迷惑的命名规则：
精确的说，SVM分类器使用的是折叶损失（hinge loss），有时候又被称为最大边界损失（max-margin loss）。Softmax分类器使用的是交叉熵损失（cross-entropy loss）。Softmax分类器的命名是从softmax函数那里得到的，softmax函数将原始分类评分变成正的归一化数值，所有数值和为1，这样处理后交叉熵损失才能应用。注意从技术说“softmax损失（softmax loss）”是没有意义的，因为softmax只是一个压缩数值的函数。但是在这个说法常常被用来简称。

SVM 和 Softmax比较：

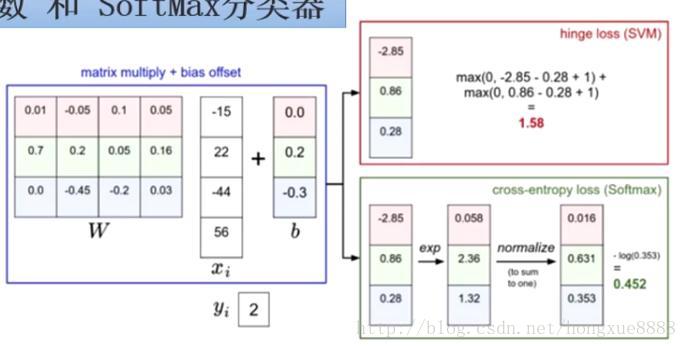
针对一个数据点，SVM和Softmax分类器的不同处理方式的例子。两个分类器都计算了同样的分值向量f（本节中是通过矩阵乘来实现）。不同之处在于对f中分值的解释：SVM分类器将他们看做是分类评分，它的损失函数鼓励正确的分类（本例中蓝色的类别2）的分值比其他分类的分值高出至少一个边界值。Softmax分类器将这些数值看做是每个分类没有归一化的对数概率，鼓励正确分类的归一化的对数概率变高，其余的变低。SVM的最终的损失值是1.58，Softmax的最终的损失值是0.452，弹药注意这两个数值没有可比性。只在给定同样数据，在同样的分类器的损失值计算中，他们才有意义。

Softmax分类器为每个分类提供了“可能性”：SVM的计算式无标定的，而且难以针对所有分类的评分值给出直观解释。Softmax分类器则不同，它允许我们计算出对于所有分类标签的可能性。举个例子，针对给出的图像，SVM分类器可能给你的是一个[12.5,0.6,-23.0]对应分类“猫”、“狗”，“船”。而softmax分类器可以计算出这三个标签的“可能性”是[0.9,0.09,0.01]，这就让你能看出对于不同分类准确性的把握。为什么我们要在“可能性”上面打引号呢？这是因为可能性分布的集中或离散程度是由正则化参数 λ 直接决定的， λ 是你能直接控制的一个输入参数。举个例子，假设3个分类的原始分数是[1,-2,0]，那么softmax函数就会计算：
[1,−2,0]−−>[e1,e−2,e0]=[2.71,0.14,1]−−>[0.7,0.04,0.26]

现在，如果正则化参数 λ 更大，那么权重W就会被惩罚的更多，然后他的权重数值就会更小。这样计算出来的分数也会更小，假设小了一半吧[0.5,-1,0]，那么softmax函数的计算就是：
[0.5,−1,0]−−>[e0.5,e−1,e0]=[1.65,0.37,1]−−>[0.55,0.12,0.33]

现在看起来，概率的分布就更加分散了。还有，随着正则化参数 λ 不断增强，权重数值会越来越小，最后输出的概率会接近于均匀分布。这就是说，softmax分类器算出来的概率最好是看成一种对于分类正确性的自信。和SVM一样，数字间相互比较得出的大小顺序是可以解释的，但其绝对值则难以直观解释。

在实际使用中，SVM和Softmax经常是相似的：
通常说来，两种分类器的表现差别很小，不同的人对于哪个分类器更好有不同的看法。相对于Softmax分类器，SVM更加“局部目标化（local objective）”，这既可以看做是一个特性，也可以看做是一个劣势。考虑一个评分是[10,-2,3]的数据，其中第一个分类是正确的。那么一个SVM（ Δ=1 ）会看到正确分类相较于不正确分类，已经得到了比边界值还要高的分数，它就会认为损失值是0。SVM对于数字个体的细节是不关心的：如果分数是[10–100,-100]或者[10,9,9]，对于SVM来说没什么不同，只要满足超过边界值等于1，那么损失值就等于0。
对于softmax分类器，情况则不同。对于[10,9,9]来说，计算出的损失值就远远高于[10，-100，-100]的。换句话说，softmax分类器对于分数是永远不会满意的：正确分类总能得到更高的可能性，错误分类总能得到更低的可能性，损失值总是能够更小。但是，SVM只要边界值被满足了就满意了，不会超过限制去细微的操作具体分数。这可以被看做是SVM的一种特性。举例说来，一个汽车的分类器应该把他的大量精力放在如何分辨小轿车和大卡车上，而不应该纠结于如何与青蛙进行区分，因为区分青蛙得到的评分已经足够低了。

章末小节：

1. 定义了从图像像素映射到不同类别的分类评分的评分函数。在本节中，评分函数是一个基于权重W和偏差b的线性函数。
2. 与KNN分类器不同，参数方法的优势在于一旦通过训练学习到了参数，就可以将训练数据丢弃了。同时该方法对于心得测试数据的预测非常快，因为只需要与权重W进行一个矩阵乘法运算。
3. 介绍了偏差技巧，让我们能够将偏差向量和权重矩阵合二为一，然后就可以只跟踪一个矩阵。

4. 定义了损失函数（介绍了SVM和Softmax线性分类器最常用的2个损失函数）。损失函数能够衡量给出的参数集和训练集数据真实类别情况之间的一致性。在损失函数的定义中可以看到，对于训练集数据做出良好预测与得到一个足够低的损失值这两件事是等价的。

   现在我们知道了如何基于参数，将数据集中的图像映射成为分类的评分，也知道了两种不同的损失函数，他们都能用来衡量算法分类预测的质量。但是，如何高效地得到能够使损失值最小的参数呢？这个求得最优参数的过程被称为最优化，将在下节介绍。