迁移学习

迁移学习Tradaboost，TCA，JDA算法简介

1、迁移学习简介

1.1 迁移学习定义

1.2 迁移学习数学表示

1.3. 迁移学习的矩阵形式

source domain:⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢x11x21⋮⋮xn1⋯⋯⋱⋱⋯x1kx2k⋮⋮xnk⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢y1y2⋮⋮yn⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥ s o u r c e   d o m a i n : [ x 11 ⋯ x 1 k x 21 ⋯ x 2 k ⋮ ⋱ ⋮ ⋮ ⋱ ⋮ x n 1 ⋯ x n k ] [ y 1 y 2 ⋮ ⋮ y n ]

Target domain:⎡⎣⎢⎢⎢⎢⎢x11x21⋮xm1⋯⋯⋱⋯x1kx2k⋮xmk⎤⎦⎥⎥⎥⎥⎥⎡⎣⎢⎢⎢⎢y1y2⋮ym⎤⎦⎥⎥⎥⎥ T a r g e t   d o m a i n : [ x 11 ⋯ x 1 k x 21 ⋯ x 2 k ⋮ ⋱ ⋮ x m 1 ⋯ x m k ] [ y 1 y 2 ⋮ y m ]

1.4 传统解决方案

方案1，只用源域数据做训练集 X: X_src， Y : Y_src
方案2，只用目标域数据做训练集合 X：X_tar, Y: Y_tar
方案3，同时利用源域数据和目标域数据做训练集合: [X_src; X_tar] Y: [Y_src;Y_tar]
方案4： X: X_src, Y: Y_src -> model_src ; X: X_tar, Y: Y_tar -> model_tar ; 然后进行模型融合
方案5： 利用xgboost，

Trate=0.15 
params = {'booster':'gbtree',
              'eta': 0.5, 
              'max_depth': 5,                  
              'max_delta_step': 0,
              'subsample':0.8,              
              'colsample_bytree': 0.8,      
              'base_score': Trate, 
              'objective': 'binary:logistic', 
              'lambda':3,
              'alpha':8
              }
params['eval_metric'] = 'auc'  
model_phase_1 = xgb.train(params,xgb.DMatrix(a_train_dummy_final,label=a_labels),num_boost_round=1000,evals=watchlist,early_stopping_rounds=100,maximize=True,verbose_eval=True)

Trate=0.2 
params = {'booster':'gbtree',
              'eta': 0.05, 
              'max_depth': 4,                  
              'max_delta_step': 0,
              'subsample':1,              
              'colsample_bytree': 0.9,      
              'base_score': Trate, 
              'objective': 'binary:logistic', 
              'lambda':3,
              'alpha':5
              }
params['eval_metric'] = 'auc' 
model_phase_1_cla_1 = xgb.train(params,xgb.DMatrix(b_train_dummy_final,b_labels),\
    num_boost_round=25,xgb_model =model_phase_1,maximize=True,verbose_eval=True)

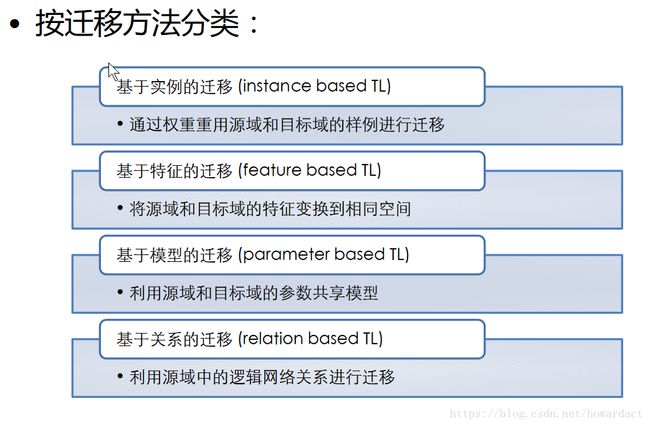
1.5. 迁移学习分类

2 Tradaboost 算法

2.1 Tradaboost算法简介

Tradaboost算法属于基于样本的迁移学习。利用AdaBoost算法的思想原理来解决这个问题，起初给训练数据T中的每一个样例都赋予一个权重，当一个目标域中的样本被错误的分类之后，我们认为这个样本是很难分类的，于是乎可以加大这个样本的权重，这样在下一次的训练中这个样本所占的比重就更大了，这一点和基本的AdaBoost算法的思想是一样的。如果源域数据集中的一个样本被错误的分类了，我们认为这个样本对于目标数据是很不同的，我们就降低这个数据在样本中所占的权重，降低这个样本在分类器中所占的比重。

2.2 Tradaboost 算法流程

2.3 Tradaboost算法核心代码

def tradaboost(Ta,label_a,Tb,label_b,test,N = 10):
    T = np.concatenate([Ta,Tb], axis = 0)
    label = np.concatenate([label_a,label_b], axis = 0)
    n = Ta.shape[0] #n为老样本量
    m = Tb.shape[0] #m为新样本量
    N = 10 # N为迭代次数
    w = np.concatenate([np.ones(n)/n,np.ones(m)/m],axis=0)
    betas = np.zeros(N)
    beta_0 = 1.0/(1.0 + np.sqrt(2.0 * np.log(float(n)/N)))
    clf = tree.DecisionTreeClassifier(criterion="gini", \
        max_features="log2", splitter="random",random_state = 99)
    #clf = LogisticRegression(penalty='l1',C=0.003,random_state = 99)
    for t in range(N):
        p = w / sum(w)
        clf = clf.fit(T, label, sample_weight=p)
        T_pred = clf.predict(T)  #待优化
        Ta_pred = T_pred[:n]
        Tb_pred = T_pred[n:]
        error_rate = sum(w[n:] * np.abs(Tb_pred - label_b) / sum(w[n:]))
        print 'error_rate: ', error_rate
        if error_rate > 0.5:
            error_rate = 0.5
        if error_rate == 0:
            N = t
            break  # 防止过拟合
        beta = error_rate/(1-error_rate)
        betas[t] = beta
        w[:n] = w[:n] * np.power(beta_0, np.abs(Ta_pred - label_a))
        w[n:] = w[n:] * np.power(beta, -np.abs(Tb_pred - label_b))
    sN2b = sum(np.log(1.0/betas[N/2:]))
    htx = clf.predict(test)
    y_predict = [1 if i >

3、 Joint Distribution Adaptation（JDA）算法

3.1 特征值特征向量

我们再来从数学定义上尝试去理解。对应一个给定的矩阵A，如果有一个向量v，使得矩阵A作用于v之后（即A和v相乘），得到的新向量和v仍然保持在同一直线上，像下面这样：

Av=λv A v = λ v

那么就称向量v是矩阵A的一个特征向量，而λ就是特征向量v对应的特征值【一个特征向量一定对应有一个特征值】。
假设A为n维的方阵，那么就会有n对特征值特征向量，特征值越大， Av A v 包含的原始信息越多。

3.2 广义特征值特征向量

Av=λBv A v = λ B v

A，B为给定的矩阵， λ λ 为某一特征值， v v 为某一特征向量。求出全部特征向量后,可以组成特征向量矩阵 V，对在保留原始信息的基础上对原始矩阵A变换降维操作。

3.3 JDA算法原理

3.3.1 基本思想

那么，JDA方法的目标就是，寻找一个变换 A A ，使得经过变换后的 P(A⊤xs) P ( A ⊤ x s ) 和 P(A⊤xt) P ( A ⊤ x t ) 的距离能够尽可能地接近，同时， P(ys|A⊤xs) P ( y s | A ⊤ x s ) 和 P(yt|A⊤xt) P ( y t | A ⊤ x t ) 的距离也要小。很自然地，这个方法也就分成了两个步骤。

3.3.2 边缘分布适配

MMD距离是

∥∥∥1n∑i=1nA⊤xsi−1m∑i=1mA⊤xti∥∥∥2H ‖ 1 n ∑ i = 1 n A ⊤ x s i − 1 m ∑ i = 1 m A ⊤ x t i ‖ H 2

这个式子实在不好求解。我们引入核方法，化简这个式子，它就变成了

D(Ds,Dt)=tr(A⊤XM0X⊤A) D ( D s , D t ) = t r ( A ⊤ X M 0 X ⊤ A )

其中 A A 就是变换矩阵，我们把它加黑加粗， X X 是源域和目标域合并起来的数据。 M0 M 0 是一个MMD矩阵：

(M0)ij=⎧⎩⎨⎪⎪⎪⎪1n2,1m2,−1mn,xi,xj∈Dsxi,xj∈Dtotherwise ( M 0 ) i j = { 1 n 2 , x i , x j ∈ D s 1 m 2 , x i , x j ∈ D t − 1 m n , otherwise

n,m分别是源域和目标域样本的个数。

好了，到此为了没有什么创新点，因为这就是一个TCA，杨强老师已经做完了。

3.3.3 条件分布适配

这是我们要做的第二个目标，适配源域和目标域的条件概率分布。也就是说，还是要找一个变换 A A ，使得 P(ys|A⊤xs) P ( y s | A ⊤ x s ) 和 P(yt|A⊤xt) P ( y t | A ⊤ x t ) 的距离也要小。那么简单了，我们再用一遍MMD啊。可是问题来了：我们的目标域里，没有 yt y t ，没法求目标域的条件分布！

能不能有别的办法可以逼近这个条件概率？根据贝叶斯公式 P(yt|xt)=p(yt)p(xt|yt)P(xt) P ( y t | x t ) = p ( y t ) p ( x t | y t ) P ( x t ) ，我们如果忽略 p(yt)P(xt) p ( y t ) P ( x t ) ，那么岂不是就可以用 P(xt|yt) P ( x t | y t ) 来近似 P(yt|xt) P ( y t | x t ) ？

而这样的近似也不是空穴来风。在统计学上，有一个东西叫做充分统计量，它是什么意思呢？大概意思就是说，如果样本里有太多的东西未知，样本足够好，我们就能够从中选择一些统计量，近似地代替我们要估计的分布。好了，我们为近似找到了理论依据。

我们依然没有 yt y t 。采用的方法是，用 (xs,ys) ( x s , y s ) 来训练一个简单的分类器（比如knn、逻辑回归），到 xt x t 上直接进行预测。总能够得到一些伪标签 y^t y ^ t 的吧。我们根据伪标签来计算，这个问题就可解了。

∑c=1C∥∥∥∥∥1nc∑xsi∈D(c)sA⊤xsi−1mc∑xti∈D(c)tA⊤xti∥∥∥∥∥2H ∑ c = 1 C ‖ 1 n c ∑ x s i ∈ D s ( c ) A ⊤ x s i − 1 m c ∑ x t i ∈ D t ( c ) A ⊤ x t i ‖ H 2

其中， nc,mc n c , m c 分别标识源域和目标域中来自第c类的样本个数。同样地我们用核方法，得到了下面的式子

∑c=1Ctr(A⊤XMcX⊤A) ∑ c = 1 C t r ( A ⊤ X M c X ⊤ A )

其中 Mc M c 为

(Mc)ij=⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪1n2c,1m2c,−1mcnc,0,xi,xj∈D(c)sxi,xj∈D(c)t{xi∈D(c)s,xj∈D(c)txi∈D(c)t,xj∈D(c)sotherwise ( M c ) i j = { 1 n c 2 , x i , x j ∈ D s ( c ) 1 m c 2 , x i , x j ∈ D t ( c ) − 1 m c n c , { x i ∈ D s ( c ) , x j ∈ D t ( c ) x i ∈ D t ( c ) , x j ∈ D s ( c ) 0 , otherwise

3.3.4 学习策略

现在我们把两个距离结合起来，得到了一个总的优化目标：

min∑c=0Ctr(A⊤XMcX⊤A)+λ∥A∥2F min ∑ c = 0 C t r ( A ⊤ X M c X ⊤ A ) + λ ‖ A ‖ F 2

看到没，通过 c=0⋯C c = 0 ⋯ C 就把两个距离统一起来了！其中的 λ∥A∥2F λ ‖ A ‖ F 2 是正则项，使得模型良好定义。

我们还缺一个限制条件，不然这个问题无法解。限制条件是什么呢？和TCA一样，变换前后数据的方差要维持不变。怎么求数据的方差呢，还和TCA一样： A⊤XHX⊤A=I A ⊤ X H X ⊤ A = I ，其中的 H H 也是中心矩阵， I I 是单位矩阵。也就是说，我们又添加了一个优化目标是要 maxA⊤XHX⊤A max A ⊤ X H X ⊤ A （这一个步骤等价于PCA了）。和原来的优化目标合并，我们就是要好了，统一写一下优化目标

min∑Cc=0tr(A⊤XMcX⊤A)+λ∥AA⊤XHX⊤A min ∑ c = 0 C t r ( A ⊤ X M c X ⊤ A ) + λ ‖ A A ⊤ X H X ⊤ A

这个式子实在不好求解。怎么弄啊，这么一大串。也不用惆怅，有个东西叫做rayleigh quotient，上面两个一样的这种形式。因为 A A 是可以进行拉伸而不改改变最终结果的，而如果下面为0的话，整个式子就求不出来值了。所以，我们直接就可以让下面不变，只求上面。所以我们最终的优化问题形式搞成了

min∑c=0Ctr(A⊤XMcX⊤A)+λ∥A∥2Fs.t.A⊤XHX⊤A=I min ∑ c = 0 C t r ( A ⊤ X M c X ⊤ A ) + λ ‖ A ‖ F 2 s.t. A ⊤ X H X ⊤ A = I

怎么解？太简单了，用拉格朗日法嘛。不说了。最后变成了

(X∑c=0CMcX⊤+λI)A=XHX⊤AΦ ( X ∑ c = 0 C M c X ⊤ + λ I ) A = X H X ⊤ A Φ

其中的Φ是拉格朗日乘子。别看这个东西复杂，又有要求解的A，又有一个新加入的Φ。 其 中 的 Φ 是 拉 格 朗 日 乘 子 。 别 看 这 个 东 西 复 杂 ， 又 有 要 求 解 的 A ， 又 有 一 个 新 加 入 的 Φ 。
但是它在matlab里是可以直接解的（用eigs函数即可）。这样我们就得到了变换A，问题解决了。 但 是 它 在 m a t l a b 里 是 可 以 直 接 解 的 （ 用 e i g s 函 数 即 可 ） 。 这 样 我 们 就 得 到 了 变 换 A ， 问 题 解 决 了 。

可是伪标签终究是伪标签啊，肯定精度不高，怎么办？那好办。有个东西叫做迭代，一次不行，我们再做一次。后一次做的时候，我们用上一轮得到的标签来作伪标签。这样的目的是得到越来越好的伪标签，而参与迁移的数据是不会变的。这样往返多次，结果就自然而然好了。

3.3 JDA核心代码

    def JDA(self, Xss, Xts, Ys, Yt0):
        '''
        Parameters
        ----------
        Xs : 源域特征矩阵 (ns_sample, ns_feature)
        Xt : 目标域特征矩阵 (nt_sample, nt_feature)
        Yt : 源域标签向量 (ns_sample, 1)
        '''
        Xs = ddss(Xss.T)
        Xt = ddss(Xts.T)
        X = np.hstack((Xs ,Xt))
        X = ddss(X)
        m,n = X.shape
        _,ns = Xs.shape
        _,nt = Xt.shape
        uYs = np.unique(Ys)
        C = len(uYs)
        e = np.vstack([1./ns * np.ones((ns,1)), -1./nt * np.ones((nt,1))])
        M = np.dot(e,e.T) * C
        if any(Yt0) and len(Yt0)==nt:
            for c in uYs:
                e1 = np.zeros((ns,1))
                e1[Ys == c] = 1./sum(Ys == c)
                e2 = np.zeros((nt,1))
                e2[Yt0 ==c] = -1./sum(Yt0 ==c)
                e = np.vstack((e1 ,e2))
                e[np.isinf(e)] = 0
                M += np.dot(e,e.T)
        M = M/norm(M ,ord = 'fro' )

        # Construct centering matrix
        H = np.eye(n) - 1./(n)*np.ones((n,n))

        if self.kernelType == 'primal':
            A = np.dot(np.dot(X,M),X.T) + self.lamda * np.eye(m)
            B = np.dot(np.dot(X,H),X.T)
            Bpinv = np.linalg.pinv(B)
            BA = np.dot(Bpinv,A)
            #BA = get_BA(A,B)
            _,Vec = eigs(BA, k = self.k, which = 'SM')
            Z = np.dot(Vec.T,X)
        else:
            K = self.get_kernel(self.kernelType,2,X.T)
            A = np.dot(np.dot(K,M),K.T) + self.lamda * np.eye(n)
            B = np.dot(np.dot(K,H),K.T)
            Bpinv = np.linalg.pinv(B)
            BA = np.dot(Bpinv,A)
            #BA = get_BA(A, B)
            _,Vec = eigs(BA, k = self.k, which = 'SM')
            Z = np.dot(Vec.T,K)
        Z = ddss(Z)
        return Z

ddss = lambda x: np.dot(x,np.diag(1./np.sqrt(np.sum(x**2,axis = 0))))

def get_BA(A,B):
    B_inv = factorized(B);
    def mv(v):
        temp = np.dot(A, v)
        return B_inv(temp)
    BA = LinearOperator(A.shape, matvec = mv) # BA.matvec(x) is np.dot(inv(B),np.dot(A,x))
    return BA

4 总结

• Tradaboost:
  基于样本的迁移学习，利用源域目标域的标签信息。求解过程不断迭代，降低源域分错样本的权重，增加目标域分错样本的权重。
• TCA算法：
  基于特征的迁移学习，只对边缘分布适配，不利用源域目标域的标签特征，为无监督适配。不迭代，直接求得转换矩阵A。
• JDA算法：
  基于特征的迁移学习，同时对边缘分布和条件分布适配。当目标域不存在label值时，可通过迭代求解伪标签求解转换矩阵A。当目标域存在label时，直接求解转换矩阵A。

5、 参考

[1] 王晋东不在家知乎博客 https://zhuanlan.zhihu.com/p/27336930

[2] JDA方法原文：Long M, Wang J, Ding G, et al. Transfer feature learning with joint distribution adaptation[C]//Proceedings of the IEEE International Conference on Computer Vision. 2013: 2200-2207.

[3] TCA方法原文：Pan S J, Tsang I W, Kwok J T, et al. Domain adaptation via transfer component analysis[J]. IEEE Transactions on Neural Networks, 2011, 22(2): 199-210.

[4] Tradaboost原文： Dai W, Yang Q, Xue G R, et al. Boosting for transfer learning[C]//Proceedings of the 24th international conference on Machine learning. ACM, 2007: 193-200.