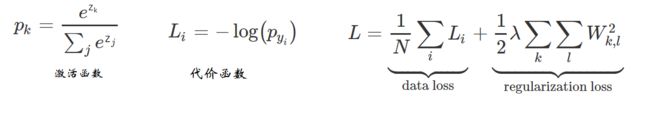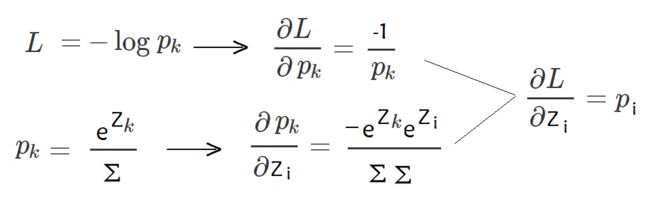SoftMax实现多分类(不含隐藏层)

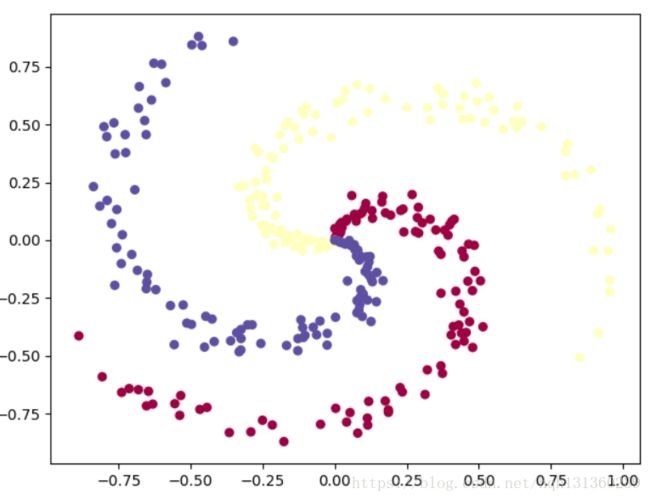
哎，看了一周，终于算是看了个大概，知其然而不知其所以然...，与LR回归不一样的是这里的分类结果是多类，这里举一个网上很常见的例子，三种类型的点各100个，对其进行分类。

1、数据生成

①数据生成没什么难点，就是中间有点小细节需要处理

②scatter的参数都是不规则写法

③只有是一维的时候reshape和转置才相同，否则不一致（没有注意到，坑了很久）

def load_data():
    np.random.seed(0)    # 每次随机数固定
    N=100                #每类100个点
    D=2                  #每个点，(x,y)
    K=3                  #3类
    X=np.zeros((300,2))
    Y=np.zeros((300,1))
    for i in range(K):
        ix = range(N * i, N * (i + 1))   #0-100、100-200、200-300
        r = np.linspace(0.0, 1, N)  # radius
        t = np.linspace(i * 4, (i + 1) * 4, N) + np.random.randn(N) * 0.2
        X[ix] = np.c_[r * np.sin(t), r * np.cos(t)]
        Y[ix] = i
    #注意：这里的c=Y，Y要转换为不规则写法，s表示点的大小，cmap表示类型
    plt.scatter(X[:, 0], X[:, 1], c=Y.squeeze(), s=30, cmap=plt.cm.Spectral)
    #plt.scatter(X[:, 0], X[:, 1], c=Y.ravel(), s=30, cmap=plt.cm.Spectral)
    #plt.scatter(X[:, 0], X[:, 1], c=Y.reshape(300), s=30, cmap=plt.cm.Spectral)
    plt.show()
    #X.T和X.reshape(2,300)不一样
    #Y.T和Y.reshpe(1,300)是一样的
    #还一个是数据类型转换，Y在传播过程中要当下表使用,计算损失函数
    return D,K,X.T,Y.reshape(1,300).astype(np.int32)

2、没有隐藏层，直接就是正向传播

softmax的正向传播的输出也与LR回归不同，有多个输出，激活函数与其它的不同，损失函数也与其它不同。主要思想如下：

①计算出Z （这里的Z是个3*300的矩阵，每一列表示为每个点的输出）

②激活函数就是操作Z为e^Z，然后归一化（列归一），计算出每种分类的概率

③损失函数，根据标签Y，Y作下标，找到每一列对应位置的概率使其经可能最大，-log(P)就是使其经可能小（注意这里只取标签位置对应的概率，也就是取300个，计算-log，然后取平均值）

④为了防止过拟合，需要加上一个正则损失

Z=np.dot(W,X)+B
A=np.exp(Z)
A=A/np.sum(A,axis=0,keepdims=True)
L=-np.log(A[Y,range(M)])         #实际标签对应的值求log、
loss=np.sum(L)/M + 0.5*reg*np.sum(W*W)

3、反向传播

反向传播最难的就是求导，k表示标签对应的概率，链式求导，dL/dZk可以求出来，同理dL/dZi=Pi（k表示标签对应的下标，i表示非标签对应的下标）(L只和Pk有关，但是Pk和Zi有关，因为Σ中包含Zi)，综合可以求出dL/dZ

A[Y, range(M)] -=1   #A表示概率P，且此操作把对应标签的概率减1，其余概率不变
dw=np.dot(A,X.T)/M
dw+=reg*W
db=np.sum(A,axis=1,keepdims=True)/M
W -= rate * dw
B -= rate * db

4、源码（一个生成数据函数，一个传播函数，一个预测函数，一个效果展示画图函数）

import numpy as np
import matplotlib.pyplot as plt
#设置画图字体
from matplotlib.font_manager import FontProperties
def load_data():
    np.random.seed(0)    # 每次随机数固定
    N=100                #每类100个点
    D=2                  #每个点，(x,y)
    K=3                  #3类
    X=np.zeros((300,2))
    Y=np.zeros((300,1))
    for i in range(K):
        ix = range(N * i, N * (i + 1))   #0-100、100-200、200-300
        r = np.linspace(0.0, 1, N)  # radius
        t = np.linspace(i * 4, (i + 1) * 4, N) + np.random.randn(N) * 0.2
        X[ix] = np.c_[r * np.sin(t), r * np.cos(t)]
        Y[ix] = i
    print(X[:, 0].shape)
    #注意：这里的c=Y，Y要转换为不规则写法，s表示点的大小，cmap表示类型
    plt.scatter(X[:, 0], X[:, 1], c=Y.squeeze(), s=30, cmap=plt.cm.Spectral)
    #plt.scatter(X[:, 0], X[:, 1], c=Y.ravel(), s=30, cmap=plt.cm.Spectral)
    #plt.scatter(X[:, 0], X[:, 1], c=Y.reshape(300), s=30, cmap=plt.cm.Spectral)
    plt.show()
    #X.T和X.reshape(2,300)不一样
    #Y.T和Y.reshpe(1,300)是一样的
    #还一个是数据类型转换，Y在传播过程中要当下表使用,计算损失函数
    return D,K,X.T,Y.reshape(1,300).astype(np.int32)
def plot_answer(model,X,Y):
    x_min, x_max = X[0, :].min() - 1, X[0, :].max() + 1
    y_min, y_max = X[1, :].min() - 1, X[1, :].max() + 1
    h = 0.01
    # xx和yy是两个大小相等的矩阵
    # xx和yy是提供坐标（xx,yy）
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    # 列扩展，每个点是一行
    Z = model(np.c_[xx.ravel(),yy.ravel()].T)
    Z = Z.reshape(xx.shape)
    # 轮廓,等高线，预测值相等的点描绘成一个轮廓，把图像进行分割
    # contour   没有颜色填充，只是分割
    # contourf  会进行颜色填充
    plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
    font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)
    plt.ylabel(u'y轴', fontproperties=font)
    plt.xlabel(u'x轴', fontproperties=font)
    plt.scatter(X[0, :], X[1, :], c=Y.squeeze(), s=30, cmap=plt.cm.Spectral)
    plt.show()
def propagation():
    M=X.shape[1]
    reg=0.001
    rate=1.0
    W=0.01*np.random.randn(K,D)
    B=np.zeros((K,1))
    for i in range(200):
        Z=np.dot(W,X)+B
        A=np.exp(Z)
        A=A/np.sum(A,axis=0,keepdims=True)
        L=-np.log(A[Y,range(M)])         #实际标签对应的值求log、
        loss=np.sum(L)/M + 0.5*reg*np.sum(W*W)
        if(i%10==0):
            print("iteration %d: loss %f" % (i, loss))
        A[Y, range(M)] -=1
        dw=np.dot(A,X.T)/M
        dw+=reg*W
        db=np.sum(A,axis=1,keepdims=True)/M
        W -= rate * dw
        B -= rate * db
    Z=np.dot(W,X)+B
    predict=np.argmax(Z,axis=0)
    print('training accuracy: %.0f%%' % (np.mean(predict == Y)*100))
    return W,B
def predict(X):
    Z=np.dot(W,X)+B
    ans=np.argmax(Z,axis=0)
    return ans
D,K,X,Y=load_data()
W,B=propagation()
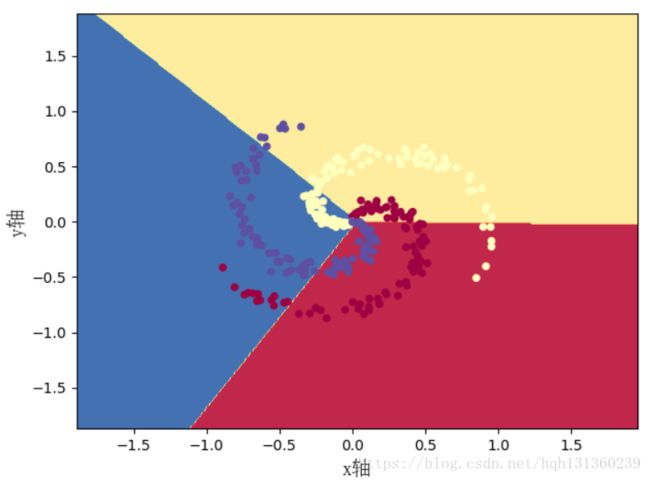
plot_answer(lambda x: predict(x),X,Y)

总结：

①激活函数、损失函数、反向传播（激活函数就是先指数操作，再归一化求概率，损失函数就是-log，损失函数操作的是正确标签对应的概率，反向传播，链式求导，一步一步慢慢推）

②遇到的问题和学习到的知识（np.argmax、np.argsort，终于知道python的强大了，不需要二维排序，直接可以使用argmax求出最大概率的下标是多少、或者求出下标的排序结果。）（转置和reshape可不是同一个概念）（A[1][:]和A[1,:]的使用，遍历时支持后者）（标签Y的数据类型的转换，因为要当下标使用，A.dtype#查看数据类型，A为Numpy类型。A.astype(np.float64)#转换数据类型。A.astype(np.int32/np.int64)  #转换数据类型）

③准确率才49%，需要添加隐藏层才能进一步提高准确率