从线性回归开始到BP神经网络到CNN卷积神经网络,代码层面剖析
1.1 CNN卷积神经网络原理
1.1.1从BP神经网络开始
BP(Backpropagation)神经网络,是一种典型的基于反向传播的神经网络。首先前向传播是比较容易的,其实就是多个线性的分类器的融合。
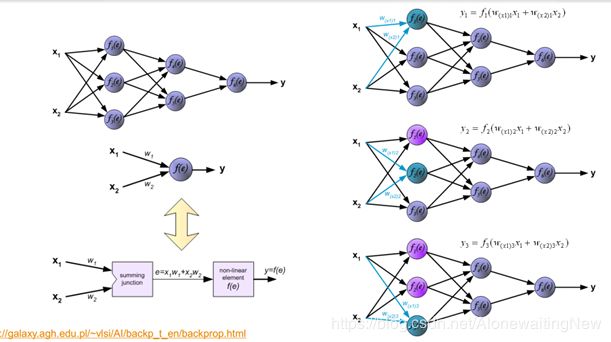
在了解神经网络之前先了解一下线性分类器。最简单的线性回归。我们先假设存在一组数据 输入为x1,x2,x3,…xn. 输出为y.我们是不是可以假设他们之间存在一种线性的函数关系呢?即:

这样一来我们就建立了从x到y的映射关系,只要计算出 即可。我们可以这样衡量,有一组数据x,通过关系式我们能得到一个y,比较计算的 y和实际的y相比,使得其值最小。最小二乘法再次奏效。

然后回到BP神经网络,对于第一层,我们是不是可以理解为多个线性分类器的叠加得到第二层,然后第二层继续按照此方法继续下去。这样一来就完成了前向传播。而我们需要的计算是每一层中w的值(也就是线性回归中的 )
对于最后一层向倒数第二层反向传播的时候我们可以计算一个差值,即实际值和计算值的差值,然后依次反向传播,每次反向传播都使用一次牛顿迭代(也叫梯度下降)如下图所示:


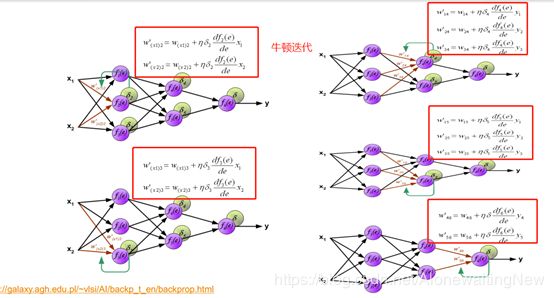
我们从线性回归可以看出,所谓的反向传播只是在寻找一个使得w下降最快的方法,而其中就用到的是最速下降法。那会不会其他的优化算法呢?问题就回到了线性回归,我们是否可以通过其他的优化算法得到这一组权重,肯定是有的,比如一些常见的智能算法遗传算法,蚁群算法。但是这些算法下降速度就比牛顿迭代法快吗?有待验证。但有一点可以肯定,使用智能优化算法就不需要反向传播了。对于深层的神经网络而言,这肯定是比较好的。如下图所示:
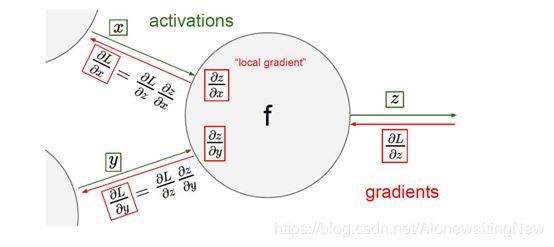
在反向传播的时候有一个链式求导法则,如果有任意一个偏导非常小,那么它传播值也会非常小,这种小会一直向后传播,而且会一直影响到后来的值。比如有一个地方的偏导等于0,那么对于后面的导数不论等于何值都是无意义的。
1.1.2CNN卷积神经网络
在图像处理中我们常用到卷积,比如Laplace算子,Sobel算子,Gaussian算子等。而这些特殊的算子能让我们得到不同的结果,比如laplace算子适合求边缘,sobel有x方向的梯度,y方向的梯度两个算子。

下面就是卷积神经网络的网络结构。
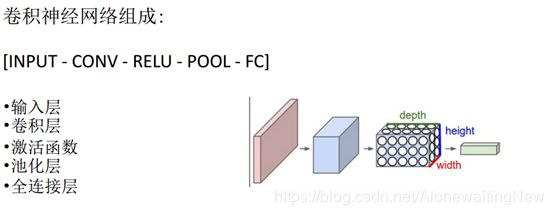
从输入到卷积层,进行的就是图像的卷积操作,然后经过一个非线性的激活函数,再经过一个pooling池化层,最后就是和BP神经网络类似的全连接层。
卷积层:顾名思义就是对图像进行一个卷积,比如一个32x32x1的图像(1表示图像的深度为1,即通道数),和一个5x5的卷积核做卷积之后的结果是28x28x1。但是有时候我们需要对边缘数据提取,这个时候我们就需要对最外层增加一个pad,也就是在最外层补上一圈或者多圈的0.如下图所示:

这样一来32x32就成了34x34,则卷积后的结果就是30x30.这些我们都是讨论卷积窗口的步长为1的情况,假设步长为2,为3呢?则卷积后的图像会更小。但我们可以得到以下公式:
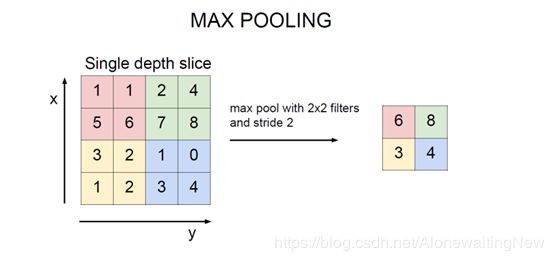
 池化层:对于一副图像来说,其数据量是极大的,我们不可能不断的去求卷积的方式使得其H和W降下来,那有没有更快得方法使得其数据量减小得更快呢?显然是有的。我们可以在一个较小得窗口内选择一个最大得数字作为该窗口的替换值,这是不是和图像卷积类似呢?是的。但是这比卷积效率更高。这种方法称为max pooling。当然还有很多其他的方法,比如用均值代替,用最小值代替等。这和图像的膨胀和腐蚀有相同之处。相当于把根号的特征保留下来了。
池化层:对于一副图像来说,其数据量是极大的,我们不可能不断的去求卷积的方式使得其H和W降下来,那有没有更快得方法使得其数据量减小得更快呢?显然是有的。我们可以在一个较小得窗口内选择一个最大得数字作为该窗口的替换值,这是不是和图像卷积类似呢?是的。但是这比卷积效率更高。这种方法称为max pooling。当然还有很多其他的方法,比如用均值代替,用最小值代替等。这和图像的膨胀和腐蚀有相同之处。相当于把根号的特征保留下来了。
全连接层:和BP神经网络类似了。
这样一来就完成了一个前向传播,我们可以建立一个简单的神经网络,然后把每一步的结果显示出来,用一张图片最为范例。
卷积层代码演示
首先是卷积层:我们定义5个7x7x3的卷积核,然后用5个卷积核分别混合原图做卷积。Pad选择为1,步长为1。
import numpy as np
import cv2 as cv
def conv_forward_naive(x, w, b, conv_param):
stride, pad = conv_param['stride'], conv_param['pad']#获取步长和pad项
H,W,C = x.shape #输入数组的总大小N,通道数C,高度H,宽度W
N=1#因为测试,选择一张图片
F, HH, WW ,C= w.shape#特征数5,通道数C,高度H,宽度WW,因为通道数必须保证相等所以都用C表示
x_padded = np.pad(x, ( (pad, pad), (pad, pad),(0, 0)),'constant')#先给图像的周围加上一圈pad
H_new = int(1 + (H + 2 * pad - HH) / stride)#计算H,W的值,该值为卷积之后的值
W_new = int(1 + (W + 2 * pad - WW) / stride)
s = stride#步长
out = np.zeros((N, F, H_new, W_new))#卷积后的结果
for i in range(N): # ith image 图像的个数
for f in range(F): # fth filter 卷积层的个数
for j in range(H_new):
for k in range(W_new):
#print(w[f].shape)
#print(x_padded.shape)
#print np.sum((x_padded[i, :, j*s:HH+j*s, k*s:WW+k*s] * w[f]))
print(f)
out[i, f, j, k] = np.sum(x_padded[j*s:HH+j*s, k*s:WW+k*s,:] * w[f]) + b[f]#简单的把对应区域和权重进行加权求和,把中心点作为求和后的结果
cache = (x, w, b, conv_param)#把输入参数保存下来
return out, cache
#归一化处理,把计算的值转到0-255范围利于保存
def normlizeation(x,xmin=0,xmax=255):
x=np.array(x)
xmax1 = np.max(x)#所有数据中最大的
xmin1 = np.min(x)#所有数据中最小的
for i in range(x.shape[0]):
for j in range(x.shape[1]):
x[i][j] = round((xmax - xmin) * ((x[i][j] - xmin1) / (xmax1 - xmin1))+xmin)
return x
adress = "D:\\My code\\Python\\opencv\\study\\01.jpg"
img = cv.imread(adress,-1)
cv.namedWindow("img",cv.WINDOW_NORMAL)
cv.imshow("img",img)
cv.waitKey(0)
#下采样 下采样降低图像大小
dst = cv.pyrDown(img)
for i in range(2):
dst = cv.pyrDown(dst)
cv.namedWindow("img",cv.WINDOW_NORMAL)
cv.imshow("img",dst)
cv.waitKey(0)
conv_param={'stride':1,'pad':1}
W1 = 1e-3 * np.random.randn(5, 7,7,3) # 生成一个5*3*7*7的权重一共5个,每个大小未7*7*3, 随机生成
B1 = np.zeros(5)
out = conv_forward_naive(dst,W1,B1,conv_param)#卷积操作
out=np.array(out)
out1 = out[0][0]#选择卷积操作后的结果
for i in range(out1.shape[0]):
img2 = out1[i]
img2=normlizeation(img2)#规整到0-255
img2=np.array(img2,np.uint8)#类型转换到unit8 ,imshow才能显示
cv.namedWindow("out",cv.WINDOW_NORMAL)
cv.imshow("out",img2)
cv.waitKey(0)
首先对原图进行下采样,然后对下采样的图像分别用四个卷积核进行计算。得到的结果分别是后面的四副图像。在调试模式下能够关注到每个矩阵维度和行列的变化。如果给更多的卷积核便能得到更多的特征图。(注意卷积核都是随机生成的,所以才有方向传播调整卷积核的数值)
激活函数:激活函数相对简单,对矩阵遍历,如果大于0的留下,小于0的置0
池化层:和卷积层类似
全连接层:有点类似BP和线性回归。
反向传播

反向传播的目的:更新参数w。因此要先算出dJ/dw。假设上一层会传过来一个梯度dJ/dout,根据链式求导法则,因此dJ/dw = dJ/dout * dout/dw =dJ/dout * x 。在计算机中方便为变量命名的缘故,将dJ/dout记为dout,dJ/dw记为dw,即图中的情况。后面也用这个记号来讲。
首先要清楚:dw 和 w 的尺寸是一样的。一个点乘以一个区域还能得到一个区域。那么反向传播过程就相当于:用dout中的一个元素乘以输入层划窗里的矩阵便得到一个dw矩阵;然后滑动滑窗,继续求下一个dw,依次下去,最后将得到的多个dw相加,执行 w = w - dw 就完成了反向传播的计算。
上面的反向传播可以更新一个filter中的参数,还要求其他的filter。
下面用图示来看一下2种不同的pooling过程——池化层的前向传播:
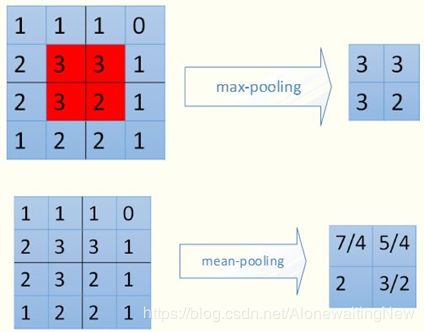 对于mean-pooling,我们需要把残差平均分成2*2=4份,传递到前边小区域的4个单元即可。具体过程如图:
对于mean-pooling,我们需要把残差平均分成2*2=4份,传递到前边小区域的4个单元即可。具体过程如图:

反向传播可以理解为一个正向传播的逆过程。和BP的反向传播以及线性回归的迭代思路是一致的。
小结
1.简单的对近期学习的卷积神经网络进行一个总结,也是一个基础性的学习,如果问题希望大家能够多多指出。
参考bolghttps://blog.csdn.net/weixin_42451919/article/details/81381294
2.为方便大家测试下载,提供源码与数据集,适合版本为Python3.0以上https://download.csdn.net/download/alonewaitingnew/11457366

