【算法系列一】霍夫曼压缩
既然是从霍夫曼压缩入手的,就先来看看它是个什么东西:
一种压缩算法,用较少的比特表示出现频率高的字符,用较多的比特表示出现频率低的字符。
它的大致过程是这样的:
- 假设压缩
“beep boop beer!” 计算字符频次,由小到大排序,得到Priority Queue
字符 次数 ‘r’ 1 ‘!’ 1 ‘p’ 2 ‘o’ 2 ‘ ‘ 2 ‘b’ 3 ‘e’ 4 每次取前两个节点,分别作为左、右节点,次数相加合并为根节点,将根节点按由小到大的顺序插入Priority Queue,由此生成二叉树
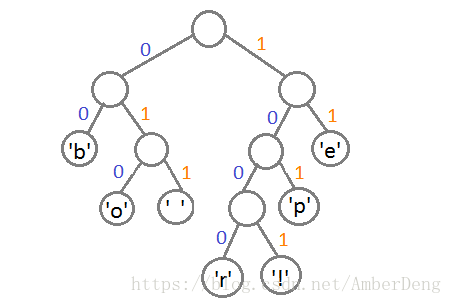
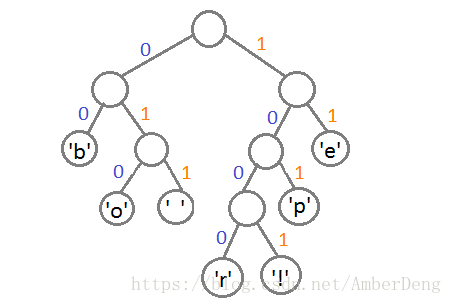
将二叉树左支编码0,右支编码1,由路径得出字符的编码
字符 编码 ‘b’ 00 ‘e’ 11 ‘p’ 101 ‘ ‘ 011 ‘o’ 010 ‘r’ 1000 ‘!’ 1001
详细过程见参考2
Python代码如下(基本思路和上述过程一致,利用堆的特性操作数据,每次执行得到的具体树和编码不保证相同):
class HuffmanCompression:
class Trie:
def __init__(self, val, char=''):
self.val = val # 节点的权重
self.char = char # 字符节点对应的字符
self.coding = '' # 字符最后得到的编码
self.left = self.right = None
def __lt__(self, other):
return self.val < other.val
def __repr__(self):
char = self.char
if self.char == '':
char = '-'
if self.char == ' ':
char = '\' \''
return char + ': ' + str(self.val)
def __init__(self, string):
self.string = string
counter = collections.Counter(string)
heap = []
# 构造二叉树
for char, cnt in counter.items():
heapq.heappush(heap, HuffmanCompression.Trie(cnt, char))
while len(heap) != 1:
left = heapq.heappop(heap)
right = heapq.heappop(heap)
trie = HuffmanCompression.Trie(left.val + right.val) # 合并的根节点
trie.left, trie.right = left, right
heapq.heappush(heap, trie)
self.root = heap[0]
self.s2b = {}
# 遍历二叉树,得到编码
self.bfs_encode(self.root, self.s2b)
def bfs_encode(self, root, s2b):
queue = collections.deque()
queue.append(root)
while queue:
node = queue.popleft()
if node.char:
s2b[node.char] = node.coding
continue
if node.left:
node.left.coding = node.coding + '0'
queue.append(node.left)
if node.right:
node.right.coding = node.coding + '1'
queue.append(node.right)
def compress(self):
bits = ''
for char in self.string:
bits += self.s2b[char]
return bits
def uncompress(self, bits):
string = ''
root = self.root
for bit in bits:
if bit == '0':
root = root.left
else:
root = root.right
if root.char:
string += root.char
root = self.root
return string
s = 'beep boop beer!'
# huffman compression
hc = HuffmanCompression(s)
compressed = hc.compress()
print('Compressed binary: ' + compressed)
print('Uncompressed: ' + hc.uncompress(compressed))
print(hc.s2b)作为一名计算机小白,对堆的概念并不太熟悉,这里补充下堆的相关知识:
数据结构中的堆(二叉堆)通常指的是完全二叉树。完全二叉树除了底层,每一层都是满的,因此可以用数组存放,且便于计算父、子节点下标。python中实现的二叉堆是最小堆,父节点值 <= 子节点值(最大堆相反)。所以每次 heappush 时,会将数据插入到正确的位置,以满足堆排序:
def testHeapq(heap):
res = []
for val in heap:
heapq.heappush(res, val)
print(res)
show_tree(res)
return res
testHeapq([3, 6, 4, 7, 1, 0])
"""
[3]
3
------------------------------------
[3, 6]
3
6
------------------------------------
[3, 6, 4]
3
6 4
------------------------------------
[3, 6, 4, 7]
3
6 4
7
------------------------------------
[1, 3, 4, 7, 6]
1
3 4
7 6
------------------------------------
[0, 3, 1, 7, 6, 4]
0
3 1
7 6 4
------------------------------------
"""heappop 就是从堆中弹出最小值了,也就是根节点。
这里就简单地介绍 heappush 和 heappop 两个基本方法,更多参见python文档
有童鞋又会问了,那堆排序如何实现呢?以最大堆为例,分3步走:
最大堆调整(Max-Heapify):子树均满足最大堆特性的前提下,保证树的最大堆特性
创建最大堆(Build-Max-Heap):从最后节点的父节点开始,自下而上 Max-Heapify
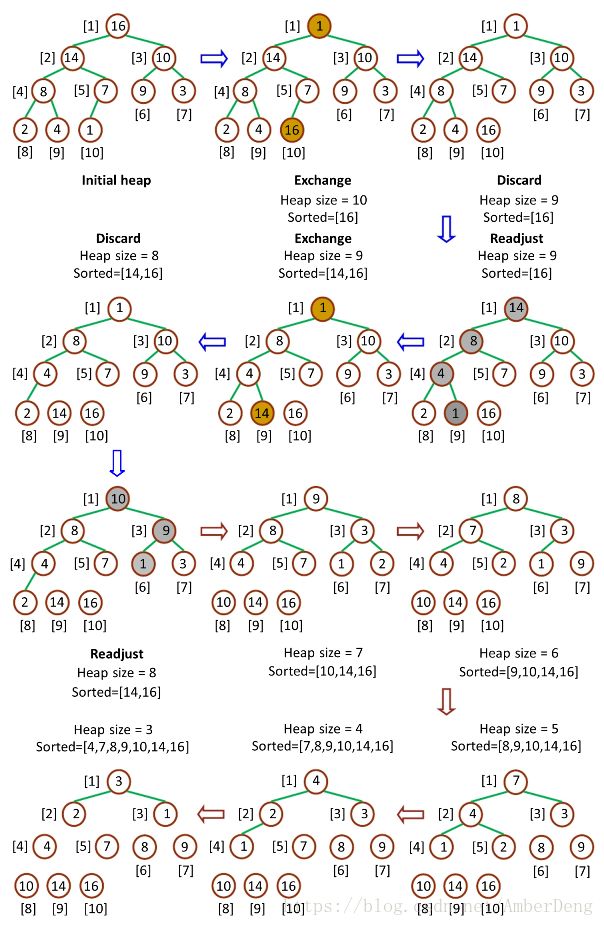
堆排序(Heap-Sort):依次互换堆顶、堆底,剔除最大值,从根 Max-Heapify
代码见heapSort
参考:
1. Huffman Compression - 霍夫曼压缩
2. HUFFMAN 编码压缩算法——详细描述了算法的执行过程
3. 常见排序算法 - 堆排序 (Heap Sort)——详细描述了堆排序的执行过程