Regularization
Regularization
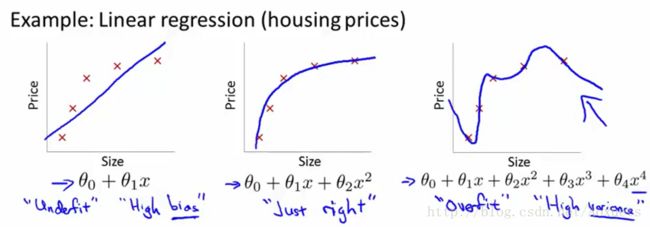
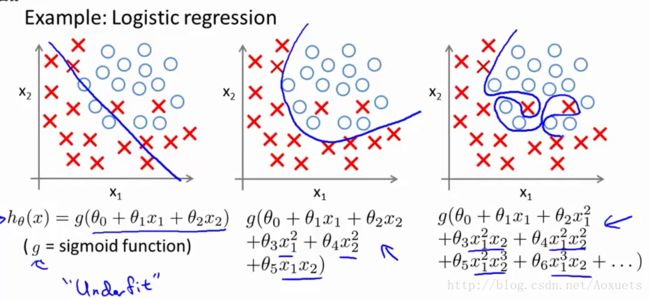
The problem of overfitting
Overfitting
if we have too many features, the learned Hypothesis may fit training set very well ( J(θ)=12m∑mi=1(hθ(x(i)−y(i))2≈0 ), but fail to generalize to new examples。
如果我们的学习函数有许多的特征, 也许这个函数可以“完美” 的拟合我们的训练数据,但这很有可能对于一个新的样本造成错误的判断。
Generalize
Generalize refer to how well a Hypothesis applies even to new examples。
泛化指学习函数适用于新样本的能力
学习函数不能很好的拟合样本 –> Underfit or High bias
出现过拟合 : Overfit or High variance
Options
- Reduce number of features.
- Manaually select which features to keep.
- Model selection algorithm
- Regularization
- Keep all the features, but reduce magnitude / values of parameters θj
- Works well when we have a lot of features, each of which contributes a bit predicting y 。
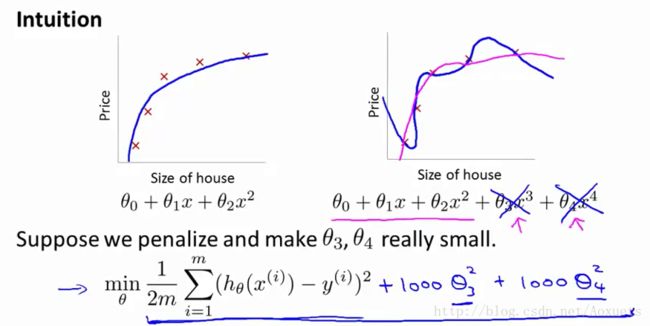
Cost Function
为了使得 CostFunction 尽可能的小, 后面的高阶多项式的系数 θ 就会要设置的尽可能的小, 几乎接近于 0, 故我们可以忽略后面的高阶多项式, 来最优化这个 Hypothesis .
为了可以使 θ 尽可能的小。我们要从新定义一下 CostFunction :
J(θ)=12m⎡⎣∑i=1m(hθ(x(i)−y(i))+λ∑j=1nθ2j⎤⎦
这里的 λ 是正规化参数。当 λ 过大时, 得到的 θ 就会趋于 0, 这样得到的预测曲线就会是一条直线, 进而变成 underfit 欠拟合。
Regularized Linear regression
Gradient descent
在普通的线性回归方程中, 我们用梯度下降算法计算 θ 的步骤如下:
θj=θj−∂∂θjJ(θ)
而对 θ 进行正规化后, Gradient Descent 如下:
Repeat{θ0θj}=θ0−α1m∑i=1m(hθ(x(i)−y(i)))x(i)0=θj−α[1m∑i=1m(hθ(x(i)−y(i)))×x(i)j+λmθj]
其实就是简单的求一次偏导。整理得
θj:=θj×(1−αλm)−α1m∑i=1m(hθ(x(i)−y(i)))×x(i)j
可以发现, 正规化其实就是把 θj 的值在每一次迭代时一点点的压缩, 后面的式子和普通的梯度下降算法没有什么区别。
Normal equation
标准方程中, 我们可以用 θ=(XTX)−1×XTY 直接得到 θ 的最优解。
而带正规化的标准方程的式子有一点变化,(根据梯度下降推导)
θ=(XTX+λ⎡⎣⎢⎢⎢⎢⎢00⋮001⋮0⋯⋯⋱⋯00⋮1⎤⎦⎥⎥⎥⎥⎥)−1×XTY
在进行标准方程计算的时候, (XTX) 可能是非逆的, 虽然 Octave 有 pinv 函数, 可以得到一个数值解,但是这并不是一个最优解, 只是看起来比较优的解而已, 而带上正规化,如果 λ>0 是可以证明求逆的矩阵是可逆的。
Regularized Logistics regression
Gradient descent
逻辑回归和线性回归的梯度下降算法中, 式子的形式是一样的,只是其中的 Hypothesis 不一样。
Repeat{θ0θj}=θ0−α1m∑i=1m(hθ(x(i)−y(i)))x(i)0=θj−α[1m∑i=1m(hθ(x(i)−y(i)))×x(i)j+λmθj]
在编写 Octave 的 CostFunction 的时候, 对于每一个梯度 gradient ,记得及时加上 λmθj(j>=1) 。
function [jVal, gradient] = costFunction(theta)
jVal = [code to compute (J of theta)]
gradient(1) = [code to compute (gradient1 of the theta_0)]
gradient(2) = [code to compute (gradient1 of the theta_1)]
*
*
gradient(n+1) = [code to compute (gradient1 of the theta_n)]