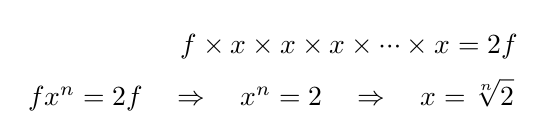译文。原文见《 Music theory for nerds》。
显然,此文不是写给那些音乐呆子看的。
我对音乐一无所知。我知道有一些字母,这些字母有时还带有波浪线;二倍频程是一个八度音程;还知道写一首流行歌曲只需要四个和弦。仅此而已。
音乐的其他知识就让我觉得极为混乱了。为什么要有 12 个音,为什么只用 7 个字母来表示它们?调号从何而来?为什么维基百科上对这些知识的介绍只有学过其他乐理知识才能读懂呢?
几天之后,我终于有点儿恍然大悟了。没能更早弄清楚,是我太白痴,不过,我觉得使用音乐记号来给那些对音乐了解甚少的人去解释音乐,毫无意义。
本文是我以小学二年级用竖笛弹奏四个音的水平整理出来的。强调这一点,旨在说明我对音乐知之甚少,这篇文章好不到哪去。倘若你口哨都吹的很好,那就没必要再看下去,不然你会笑话我。
声音与波
音乐是一种声音。声音是一种压力波。
想象一下,敲一面鼓的时候会发生什么。鼓面有弹性,因此在敲击它时,它会向内发生形变,然后又向外反弹,这个过程会持续到能量被完全释放掉时终止。位于鼓面中心的运动很像一个彩虹圈(Slinky)——它的顶端被你握住,另一端作往复运动。
当鼓面向外反弹的时候,它将空气向外推开。空气又推开更多的空气,形成了离开这面鼓的三维涟漪。同时,鼓面又向内凹陷,形成了一个真空,鼓面附近的空气会填填满它……结果又形成了真空。结果就会导致任意一个给定的空气分子从它的原始位置出发时而向内时而向外的漂移,像鼓面或彩虹圈那样。
最终,这个压力波抵达你的耳朵里的鼓膜,引发了你的鼓膜作与敲击的鼓面相同的振动,你的大脑会将这种信号解析为音乐,或噪声,这取决于你的品味。
我很想以池塘里水面上的涟漪为例直观地展示这一切,但困难之处在于涟漪是忽上忽下的运动,而声音在三维空间中是距离声源忽远忽近的运动,二者之间还是有区别的。
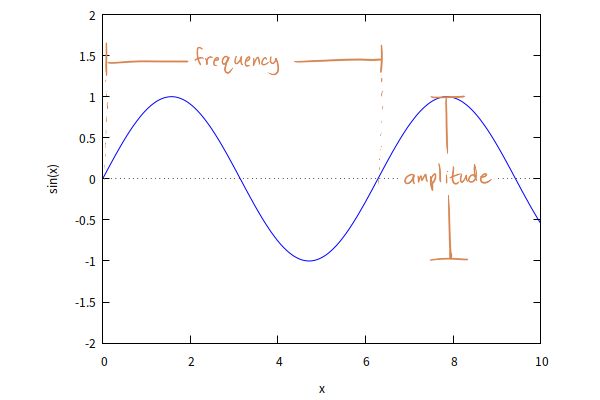
还是直接以图形的方式来展示为好。下面是一个正弦波:
这个正弦波代表了什么,我们不关心,它只是最容易画出来的常见波形。
在这样的图形中,时间从 0 开始,在横轴上向右递增。波形展示的是空气(鼓面或任何媒介)相对于它的原始位置如何运动的。运动完全的停止下来,就是纵轴坐标为 0 的那条直线。
你听过的所有声音都是像这样的图。如果你在 Audacity 中播放一首歌,把声音放得足够大,你就能听到一个波。它可能要比正弦波更复杂一些,但它依然是一个波。
波由频率、振幅和形状定义。你听到的特定声音——类似于钢琴的声音与吉他有别——就是波形,音乐家将其称为音色。
正弦波听起来就像这样:https://eev.ee/media/2016-09-15-music/sine-wave.ogg
振幅是波形的最低点与最高点之间的距离,也有人将其定义为波形最高点到 0 点之间的距离。对于声音,振幅决定了音量。这看起来很合理,因为在物理术语中,振幅是媒介移动的最远距离。如果你轻轻地敲一下鼓面,它会轻微移动,发出的声音也就很轻。如果你敲得重一些,它移动的幅度就会大一些,声音也就大一些。
频率,顾名思义就是波有多么急促。如果每个波峰与波谷都很瘦,那么波也就越急促,也就是说,它的频率就越大。如果每个波峰与波谷都很宽绰,那么波也就越舒缓,也就是说,它的频率就越小。音乐家将频率称为音高。非音乐家可能会将其称为音符或音。音乐家对嗤之以鼻,不过他们真的懂么。
频率的单位是 Hz(Hertz),它的意思是「每秒」。如果一个点从一个波上到另一个波上的相同位置上的点,用时 0.5 秒,那么波的频率就是 2,因为每秒出现了 2 个波。
人类的耳朵有一个极为重要的特性——它影响着其他特性。这个特性就是如果将声音的频率加倍或减半,我们在某种程度上会认为它没变。虽然听起来声音大一些或小一些,但是我们觉得它们很相似。对此,我可以给出一些物理成因上的猜测,不过我们还是把这当成一条随意的规则吧。
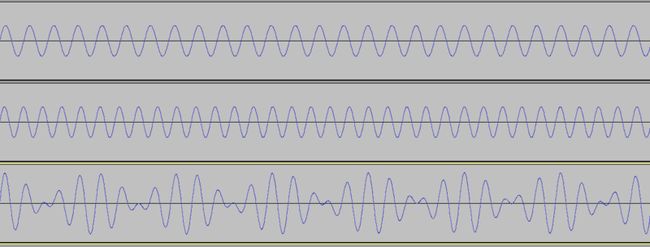
不妨对下面三个正弦波作一下比较。第一个是与前文出现的正弦波相同,第二个是第一个的 1.5x 频率,第三个是第一个的 2x 频率。第一个与第三个听起来,要比第二个与另外二者之一,更为相关。
- 440 Hz
- 660 Hz
- 880 Hz
音与八度
音乐之难,一半在于它的随意性,一半在于它的基本原理,而这二者很难区分。
我们先来考察人耳的特性:音高(频率)加倍后,听起来不变。以任意一个音高 f 作为起点,可以产生无限多个在我们听起来「相同」的声音(当然,它们得在人耳的听觉范围):f/2、2f、f/4、4f 等。这些音高有一定的共性,因此可以用一个音来指代它们(尽管在音高类别确定的情况下,音也指代单个音高,不过从现在开始我坚持使用「音」这个词)。
若 440 Hz 对应的音叫做 A,那么 880 Hz、220 Hz、1760 Hz、110 Hz 等音高对应的音也叫做 A。一个重要的结论是,能够提供给音乐的所有的不同音,必须位于 440 Hz 到 880 Hz 这个区间内。其他的任何音高皆可经过加倍或减半,变换到这个区间内,因此它们对应的音就会落入这个区间。
这个区间就是所谓的八度,至于为什么要这么叫,呆会再说。每个音在任何给定的八度内只出现一次,这与这个八度如何定义无关。最低的音高 f,它的音与 2f 相同,因此 2f 只能属于下一个八度。
这个想法很妙!这意味着我们可以在一个很小的音高范围内挑选一些音高。这个范围可以任意小,只要它介于 f 与 2f 之间即可。然后通过对所挑选的音高加倍或减半,就能够得到跨人耳听觉范围的全部的标准音集了。
不过,应当如何选择这些音高呢?你可能会说,这个容易,只需要选择 1f、1.1f、1.2f、1.3f、1.4f 等等,即等距采样,让采样频率尽可能有所区别。
想法不错,然而行不通。试一下就知道了,1f 与 1.1f 之间的差异近乎是 1.9f 与 2.0f 之间的差异的二倍。
人耳对音高的区分是按比例来的,这就是人耳具有有音高的减半或加倍效应的原因。f 到 1.1f 是 10% 的增长,而 1.9f 到 2f 是 5% 的增长。
我们需要的是一组有相同比例而不是相同距离的音高(译注:需要一个关于音高的等比数列而不是等差数列)。如果想要 n 个音高,我们需要一个数 x,让它乘以自身 n 次来形成 f 到 2f:
啊,我们需要的这个数是 2 的 n 次方根。这有点怪异和尴尬,因为在 n > 1 时,它是个无理数。
西方音乐的音程
西方音乐有 12 个不同的音高。这有些随意——12 这个数虽然有一些美妙的数学性质,但是绝非必要。你可以用 11 个,或者 17 个,或者 100 个,或者 5 个音高来创造你自己的音集。这个世界上,有些地方的音乐形式就是这样做出来的。
西方音乐里任意两个连续的音高,它们的比值是 $sqrt[12]{2} = 1.0594631$。从 440 Hz 开始重复乘以这个值直到最终结果为 880 Hz,结果可以得到下面的音高序列:
0 440 Hz
1 466.16 Hz
2 493.88 Hz
3 523.25 Hz
4 554.36 Hz
5 587.33 Hz
6 622.25 Hz
7 659.26 Hz
8 698.46 Hz
9 739.99 Hz
10 783.99 Hz
11 830.61 Hz
12 880 Hz没人愿意直接用这些数字,并且在西方音乐诞生的时候,世上还没这些数字呢。实际上,音乐的定义体现为比例的形式。
两个音高之间的比例称为音程。2 的 12 次方根,这个音程被称为半音。用这种办法,那些糟糕的无理数就华丽地消失了,我们面对的就是整数了。(实际上这种做法是在对数尺度上工作。对数可能会让许多人觉得恐惧,实际上它就是将乘法变成加法)。
现在,要记住,人耳偏爱比例。更确切地说,我们的耳朵偏爱小整数的比例。为什么加倍的音高听起来与原音高相似?这是因为你的耳朵能捕捉到的最小并且是最整数的比例,2:1。
虽然 2 的 12 次方根是一个无理数,但是它却能够创造一些优美的比例(我不知道为什么 12 会有这样的效果,也不知道换成其他数字是不是也一样,但是这可能是西方音乐扎根于 12 的原因)。下面是 12 个音的相对音高——每个音高除以第一个音高,它们中有一些很接近简单的分数:
0 1.000 = 1:1 (unison)
1 1.059 (semitone; minor second)
2 1.122 ≈ 1.125 = 9:8 (whole tone; major second)
3 1.189 (minor third)
4 1.260 ≈ 1.250 = 5:4 (major third)
5 1.335 ≈ 1.333 = 4:3 (perfect fourth)
6 1.414
7 1.498 ≈ 1.500 = 3:2 (perfect fifth)
8 1.587 (minor sixth)
9 1.682 ≈ 1.667 = 5:3 (major sixth)
10 1.782 (minor seventh)
11 1.888 ≈ 1.889 = 17:9 (major seventh)
12 2 = 2:1 (octave)若忽略 8 度音(即 2:1 对应的 Octave),那么一共有 7 个很优美的分数。
嗯,7,魔性的数字!
音阶
吃惊吧,这些美妙的分数竟然构成了大调音阶(Major Scale)。若以音 C 开头,那么就构成了 C 大调音阶——一组「自然」音。使用 来表示加上一个半音(Semitone),使用 表示减去一个半音,就可以给所有的音起名了,如下:
0 1.000 = 1:1 C (unison)
1 1.059 C or D (semitone; minor second)
2 1.122 ≈ 1.125 = 9:8 D (whole tone; major second)
3 1.189 D or E (minor third)
4 1.260 ≈ 1.250 = 5:4 E (major third)
5 1.335 ≈ 1.333 = 4:3 F (perfect fourth)
6 1.414 F or G
7 1.498 ≈ 1.500 = 3:2 G (perfect fifth)
8 1.587 G or A (minor sixth)
9 1.682 ≈ 1.667 = 5:3 A (major sixth)
10 1.782 A or B (minor seventh)
11 1.888 ≈ 1.889 = 17:9 B (major seventh)
12 2 = 2:1 C (octave)不确定这是不是这些音的现代命名的来源,即便是,我也不会惊讶。
现在,你可以看到这些音程的名字的来由了。纯五度(Pefect Fifth)就是音阶的第一个音与第五个音之间的音程。八度(Octave)跨越全部音。类似地,最小的音程是半音,因为多数音可分为两步。这两步合起来就是全音(Whole Tone)。
连续的音所形成的音程可写为 wwhwwwh,其中 w 是全音,h 是半音。由于八度的重复性,你可以「滚动」这个序列,就可以产生 7 种不同的变体,它们依赖于从哪个音开始。结果得到的这些音阶统称为自然音阶(Diatonic Scale),起点的选择称为调式(Mode)。下面给出了用罗马数字标记的 7 列音阶,它们的起点不同,因此这些音都是「自然的」。
I II III IV V VI VII
0 1.000 = 1:1 |C| D E F G |A| B
1 1.059 | | F | | C
2 1.122 ≈ 9:8 |D| E G A |B|
3 1.189 | | F G |C| D
4 1.260 ≈ 5:4 |E| A B | |
5 1.335 ≈ 4:3 |F| G A C |D| E
6 1.414 | | B | | F
7 1.498 ≈ 3:2 |G| A B C D |E|
8 1.587 | | C |F| G
9 1.682 ≈ 5:3 |A| B D E | |
10 1.782 | | C D F |G| A
11 1.888 ≈ 17:9 |B| E | |
12 2 = 2:1 |C| D E F G |A| B第 1 列与第 6 列加了「高亮」。第 1 列是大调音阶(Major Scale)。第 6 列是自然小调音阶(Natural minor scale)。有一些音程的名字可以这样解读:小三度(Minor third)就是跨小调音阶里的第 1 个到第 3 个音的音程;大三度(Major third)就是跨大调音阶里的第 1 个到第 3 个音的音程。第 4 与第 5 个音是相同的(译者:意思是说纯四度与纯五度都没有大调小调之分吧……)。(作者:第二个音也是相同的,但我不知道小二度的来由。)
按照相同的音程模式,你可以任意取一个开头来产生大调或小调音阶。使用十二音,能够生成二十四个大调与小调音阶,从而形成一个庞大驳杂的表。下面是几个大调:
A major: A B C# D E F# G# A
A# major: A# C D D# F G A A#
B major: B C# D# E F# G# A# B
C major: C D E F G A B C
C# major: C# D# F F# G# A# C C#
D major: D E F# G A B C# D
D# major: D# F G G# A# C D D#如果你滚动这些大调,让它们变成以 C 开头,结果就会变成:
A major: C# D E F# G# A B C#
A# major: C D D# F G A A# C
B major: C# D# E F# G# A# B C#
C major: C D E F G A B C
C# major: C# D# F F# G# A# C C#
D major: C# D E F# G A B C#
D# major: C D D# F G G# A# C下面是采用同样的方式构造出来的一些小调:
F# minor: C# D E F# G# A B C#
G minor: C D D# F G A A# C
G# minor: C# D# E F# G# A# B C#
A minor: C D E F G A B C
A# minor: C# D# F F# G# A# C C#
B minor: C# D E F# G A B C#
C minor: C D D# F G G# A# C看到了吧,每个大调与以倒数第二个音开头的小调相同。它们被称为彼此的相对大调与相对小调。
不过,这种记法有个小问题,会导致乐谱太糟糕。
乐谱与调号
如果你对乐谱知之甚详,你可能会注意到没有空间来写降半音或升半音。
如果你对乐谱一无所知,那么只需要知道,没有空间来写降半音或升半音。
如果你想在乐谱上写其他任何音,要把它们放到同一条线上,但是它们的后面需要跟上 或 。因此,D 大调的音包含 F 与 C,要写它们,得先写成 F 与 C,然后再放上一些 。这样做,不是很方便,所以要在开头放上调号——就是在特定位置放一些 或 ,用于表示哪些音是升或降。这样一来,乐谱中任何一个未被修饰的音就可以根据调号来确定它是升或降了。
(这些音可能不是这样安排的,这有赖于左侧的谱号(那个花里胡哨的符号)的形式与它的竖直方向上的位置。)
这样做,真的方便吗?如果你的曲子依赖于特定音阶里的 7 个音,那么在乐谱里写这 7 个音的空间就相当紧凑了,还要在需要的时候调整这些音的含义,真的可以吗?
这样做的话,会完全混淆了音高之间的关系。若非刻意去去记,某个乐谱用的是哪个音阶就不太容易判断。在上面的例子里,有面向 C 与 F 的 #;但是这能揭示这是 「D」大调么?
说这些,不过是想说说我对这种记法的一些看法。再看一下 C# 大调:
C# major: C# D# F F# G# A# C C#有两对音使用相同的字符——C 与 C#,F 与 F#——因此,它们在乐谱中就占用相同的位置。若是像上述我说的那样处理,就会出问题。
为了解决这一问题,有些音阶就作了点迂回。C 比 B 高半个音,所以可将 C 写为 B#。F 比 E 高半个音,所以可将 F 写为 E#。于是,C# 大调可写为:
C# major: C# D# (E#) F# G# A# (B#) C#这样就可以保证 7 个字符只出现一次了。对此我表示不能完全理解,因为它还是让我相当困惑。你不得不在心智上将 C 转译为 C#,再将 C# 转译为乐器上的演奏。这样做的目的是什么呢?这样做,可以让乐谱更紧凑——7 个音符表示每个八度,而不是 12 个音——我想不出来更好的理由。
仅通过改改调号来更改一段音乐的声音,而不是更换乐谱,这种做法应该是可行的。我好奇的是,对于使用了音阶之外的音的音乐,这样做能行得通么?这些问题,看上去像是一些让我难以想通的组合问题。
还有些东西,还有些东西,还有和弦
我从一团混乱中略微挣扎了一下,就到了这里。
刚才我说过,大调音阶与小调音阶总是成对出现。每个大调音阶都有一个相对的小调音阶,它们的音完全相同,反之亦然。因此,C 大调与 A 小调相同。可是,我们为啥需要两个相同的音阶呢?更重要的是,这两个音阶使用的调号相同,你该如何判断一段音乐是这两个音阶中的哪一个呢?
许多人试图从基调、不同的声音等等角度让我明白,他们只不过是将问题转移了,而不是真正地回答它。就我手头的资料来看,真正的答案有两个。
答案 1:音乐是基于一个调写出来的,这个调包含音阶和常见的和弦,可能还有别的一些成分。所谓和弦,就是几个音一起或近乎一起弹奏出来。你可以构造许多不同的和弦,但真正的大玩家是大调和弦与小调和弦,它们都是音阶中的第 1、3、5 个音。C 大调和弦(记为 C,感觉好乱)由 C、E 和 G 构成,而 A 小调和弦(记为 Am)由 A、C 和 E 构成。
大调和弦由根音、根音升 4 个半音、根音升 7 个半音构成——简而言之,即 {0, 4, 7}。小调和弦是 {0, 3, 7}。这两种和弦的第一个音与最后一个音都是相距 7 个半音,这就是所谓的纯五度(Perfect fifth),即美妙的 3:2 比例。大调和弦与小调和弦有相同的根音,它们听起来有些相似,不过由于小调和弦中间那个音略为低一些,因此它听起来通常更生动或忧悒。
话说,当你比较一下以相同的音开头的大调与小调音阶,有趣的事就出现了。它们很相似,区别仅在于大调音阶有三个音都高出一个半音。
C major: C D E F G A B C
C minor: C D D# F G G# A# C每个大调与小调音阶都有 7 个这种形式的和弦(译注:{0, 4, 7} 或 {0, 3, 7}),这取决于从哪个音开始;例如,C 大调音阶的第 2 个和弦 D-F-A,它是 D 小调和弦。没错,小调和弦;它与 D 小调音阶的第一个和弦相同。
有时,你会看到记成罗马数字形式的和弦,大写字母表示大调和弦,小写字母表示小调和弦。大调音阶的和弦是 I、ii、iii、IV、V、vi、和 vii; 小调音阶的和弦是 i、ii、III、iv、v、VI 和 VII。「I」表示和弦的根音是第一个音,其他字母的含义以此类推。这种记法会让你觉得,和弦行进不需要担心任何特定的调。
不过,这没有解释为什么要同时有 A 小调与 C 大调,于是这就需要第 2 个答案……
答案 2:仅仅是出于习惯。西方音乐的编写倾向于某些约定,对这些约定了如指掌的人很清楚什么情况下遵守哪一个约定。用 C 大调写出来的音乐,通常以 C 或 C 大调和弦开头或结尾;以 A 小调写出来的音乐 通常以 A 或 A 小调和弦开头或结尾。据我所知,这两个音集并没有什么本质上的不同,这些约定也不是硬性需求。
这样做的好处主要体现在约定上:你的工作对于同领域的人而言更容易理解。例如,让音乐在两个调之间变换,只有在你确信自己能够说出原始的调是什么的情况下有意义。
毫无疑问,这些约定有着无数的变体。和声小调(Harmonic minor scale)是 7 个音都升半个因而形成的小调音阶。旋律小调(Melodic minor scale )也调整了几个音,使之上升,而不是下降。还有增和弦(和音程),它们将最高的音提升了一个半音。减和弦,将最高的音降低一个半音。就这样,这一切都在乱七八糟的叠加着,为同一种东西演绎出来多种不一致的名字,这一切都源于他们所描述的是人类的意图,而不是客观的波形。
@@@@@
五度圈 这种东西,将所有的大调与小调音阶放在了一个圆内——它揭示了,只要以正确的方式命名与安置,那么每个音阶就会有不同数量的升半音或降半音,并且能保证升半音与降半音不能并存于一个音阶之内。「正确的方式」就是一次迭代 7 个半音(因而叫「五度圈」),也就是从 C 到 G 再到 D 这样地循环。一个音阶使用升半音还是降半音,取决于音阶里的所有的音是否具备不同的字符以及是否适于乐谱。这必定可以用模运算来解释,不过我现在没心思去研究。
@@@@@
整数的比例之所以能吸引人耳,是因为它们有时能够将波形组合起来。下面是纯五度的波形——上面两个音是基于不完全的 2 的 12 次方根的 A4 与 E5。由于它们可以形成一个 3:2 这样美妙的比例,把它们叠加到一起,就可以形成 6 个波形,这些波形本身构成了一个波。
(A4 是第 4 个八度(原文作 Octave 4,译者是音乐盲,故不知其意)中的 A 音。第 4 个八度起自中央 C(Middle C),二者之名来自钢琴键的布置。通常是将 A4 设成 440 Hz 作为调音的参考点。)
@@@@@
最后,要注意「同名」的音未见得是相同的音,它们依赖于如何对乐器进行调音;有多种模式可以让特定的和弦恰好对应着整数比例,而不是近似值。「伪造」的音比 E# 还要多;我听过像 G 这样的号称「G 双煞噗」之类的谣言,而我宁可称之为「A」。我怀疑二者有所联系,但是不明就里。
以上就是我所知道的一切了。不能知道更多。
译注:凡是带有五个
@ 的部分,我也不知道作者在说什么。
结语
这是一些最糟糕的行话与记法,永远如此。
我计较这些,是因为想合成一些音乐。对这方面的东西过于陌生,总让我觉得难以做下去。弄懂这些,或许对我要做的事没有什么帮助,不过至少解了一些困惑。
若是一个东西不能单纯的用数学与波形来表达,它的形式就会相当随意。你可以从 12 音里随意拮取一个子集,就可以用它们来制作音乐。有人指点我,如果只使用钢琴的黑键(亦即非自然音),就可以得到五声音阶,听起来也不错,因为不会有两个音因为靠得太近而形成一个音。也可以使用 12 音之外的音,就像大多数爵士、非西方、非典型性的音乐所做的那样。
我的感觉是,将整个和弦/调的体系作为一个规则集合,犹如研究文艺复兴时的绘画就可以断定什么是艺术。并非如此。做你想做的,只要听起来好听。我打算这么干。共识似乎是音乐的本质在于掌控反差,就像其他艺术形式那样。
若你尚未准备好放弃整个西方音乐的传承,在我正在努力弄懂它的时候,他人在 Twitter 上给了我一些资料,可以看看。
- 本周在数学物理中的发现,基于群论的一些东西。
- 音乐,Toby Fox 的大作,讲述的是如何为 Undertale(似乎是个游戏)制作配乐,还有 Undertale 的其他方面的东西;简短又全面地给出了观点。
- 音数学:音乐的数学基础, 33 美元的书,一些人推荐给我,但我还没买。
- 玩转音乐,从不讲音乐符号开始夸夸其谈,前六章免费;看书评,似乎对音乐合成有用,以后我可能会看看。
- 组合音乐原理,一个离开数学符号就活不下去的数学家写的一些音乐理论。
- 音乐节奏几何学:「好」节奏为何好,顾名思义的一本书。
- 来自栈交换网站音乐版的答案,尝试弄明白为什么音乐理论要这样。
- 音乐几何,上述的栈交换网站的答案认为这是最好的入门书。