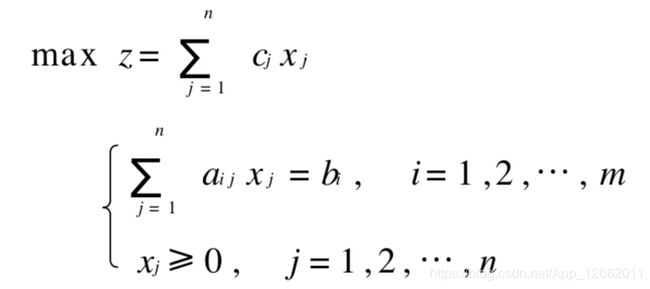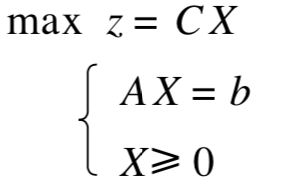运筹优化(四)--线性规划之对偶问题和灵敏度分析
线性规划的灵敏度分析,是指模型参数的变化,对优化结果的影响分析,分定性和定量两种。
定性分析
这里的定性分析,指参数变化,对结果的影响,比如不变,变坏或者变差。
松约束和紧约束
放宽优化模型中的约束条件会使模型最优值不变或者更优。收紧优化模型中的约束条件会使模型最优值不变或者更差。依据是因为修改了约束条件意味着修改了可行域,也会有新的可行解或者减少可行解。因此,体现在右端系数RHS变化,左端系数LHS变化,以及约束条件、变量的增删上。
定量分析
定量分析,就是利用对偶模型来分析原始模型的灵敏度的量化方案。即:
如果一个模型具有可以定量表示原始模型对系数变化的灵敏度的决策变量与约束条件,那么它就是原始模型的对偶模型。
也就是说,原始问题的约束条件,是对偶问题的决策变量,对偶问题的约束条件对应原始问题的决策变量。
虽然对偶模型是以灵敏度分析的目的提出,但实际上,它带来了更多有趣的信息。
对偶模型
1.原问题与对偶问题的关系
对于“≤”不等式约束条件的原问题与“≥”不等式约束条件的对偶问题的展开形式是
原问题
对偶问题
线性规划的原问题与对偶问题的关系 , 其变换形式归纳为表 2 -4 中所示的对应关系。
2.对偶问题的基本性质
(1) 对称性 对偶问题的对偶是原问题。
(2) 弱对偶性
m i n ( - ω′) = - C X ; - A X ≥ - b ; X ≥ 0 m i n ( - ω′) = m a x ω′
m a x ω′= m a x z = C X ; A X ≤ b ; X ≥ 0
若 X 是原问题的可行解, Y 是对偶问题的可行解。则存在 CX≤Yb。
(3) 无界性 若原问题(对偶问题)为无界解,则其对偶问题(原问题)无可行解。
( 4) 可行解是最优解时的性质 设 X^是原问题的可行解 , Y^是对偶问题的可行解 , 当CX^=Y^b时 ,X^,Y^是最优解 。
(5) 对偶定理 若原问题有最优解,那么对偶问题也有最优解;且目标函数值相等。
(6) 互补松弛性 若 X^, Y^分别是原问题和对偶问题的可行解。那么Y^Xs = 0和Ys X^=0,当且仅当 X^,Y^为最优解。
(7) 设原问题是maxz=CX; AX+XS =b; X,XS≥0,它的对偶问题是minw = Yb;YA-Ys = C;Y,Ys>= 0则原问题单纯形表的检验数行对应其对偶问题的一个基解 , 其对应关系见表 2 -5。
这里Ys1是对应原问题中基变量XB的剩余变量, Ys2是对应原问题中非基变量XN的剩余变量。
3.对偶问题的经济解释--影子价格
我们从上面的对偶问题与原始问题的关系可以看出,对偶问题定量表示了原始模型对系数变化的灵敏度,也就是说,对偶问题的最优解,反应了资源变化对原始目标函数值的影响,这在经济学上定义为影子价格。影子价格随具体情况而异 , 在完全市场经济的条件下 , 当某种资源的市场价低于影子价格时 , 企业应买进该资源用于扩大生产;而当某种资源的市场价高于企业影子价格时, 则企业的决策者应把已有资源卖掉。可见影子价格对市场有调节作用。
4.对偶单纯形法
根据对偶问题的对称性,可以这样考虑: 若保持对偶问题的解是基可行解, 而原问题在非可行解的基础上 , 通过逐步迭代达到基可行 解 , 这样也得到了最优解。其优点是原问题的初始解不一定是基可行解 , 可从非基可行解开始迭代 , 方法如下。
设原问题:
又设B是一个基。不失一般性,令B=(P1 ,P2 ,⋯,Pm),它对应的变量为XB =(x1 ,x2 ,⋯,xm)
当非基变量都为零时, 可以得到XB=B-1 b。若在 B-1 b中至少有一个负分量, 设 ( B-1 b)i < 0, 并且在单纯形表的检验数行中的检验数都为非正, 即对偶问题保持可行解,它的各分量是
(1)对应基变量x1,x2,⋯,xm 的检验数是σi=ci-zi=ci-CBB-1Pj=0, i=1,2,⋯,m
(2)对应非基变量xm+1,⋯,xn 的检验数是σj =cj -zj =cj -CBB-1 Pj≤0, j=m+1,⋯,n 每次迭代是将基变量中的负分量 xl 取出 , 去替换非基变量中的 xk , 经基变换 , 所有检验数仍保持非正。从原问题来看, 经过每次迭代 , 原问题由非可行解往可行解靠近。当原问题得到可行解时, 便得到了最优解。
对偶单纯形法有以下优点 :
(1) 初始解可以是非可行解,当检验数都为负数时, 就可以进行基的变换, 这时不需要加入人工变量 , 因此可以简化计算。
(2) 当变量多于约束条件,对这样的线性规划问题,用对偶单纯形法计算可以减少计算工作量 , 因此对变量较少 , 而约束条件很多的线性规划问题 , 可先将它变换成对偶问题 , 然后用对偶单纯形法求解。
(3) 在灵敏度分析及求解整数规划的割平面法中,有时需要用对偶单纯形法,这样可使问题的处理简化。对偶单纯形法的局限性主要是 , 对大多数线性规划问题 , 很难找到一 个初始可行基 , 因而这种方法在求解线性规划问题时很少单独应用。
LP的灵敏度分析
在以前讨论线性规划问题时,假定αi j , bi , cj 都是常数。但实际上这些系数往往是估计值和预测值。如市场条件一变, cj 值就会变化;αi j 往往是因工艺条件的改变而改变; bi 是根据资源投入后的经济效果决定的一种决策选择。 因此提出这样两个问题: 当这些 系数有一个或几个发生变化时 , 已求得的线性规划问题的最优解会有什么变化; 或者这些系数在什么范围内变化时,线性规划问题的最优解或最优基不变。
显然 , 当线性规划问题中某一个或几个系数发生变化后, 原来已得结果一般会发生变化。当然可以用单纯形法从头计算 , 以便得到新的最优解。这样做很麻烦 , 而且也没有必 要。因在单纯形法迭代时,每次运算都和基变量的系数矩阵B有关, 因此可以把发生变 化的个别系数,经过一定计算后直接填入最终计算表中, 并进行检查和分析。
灵敏度分析时, 主要讨论在最优基不变情况下, 确定系数 ai j , bi , cj 的变化范围。而参数线性规划是研究这些参数中某一参数连续 变化时 , 使最优解发生变化的各临界点的 值。即把某一参数作为参变量 , 而目标函数在某区间内是这个参变量的线性函数 , 含这个参变量的约束条件是线性等式或不等式。因此仍可用单纯形法和对偶单纯形法分析参数线性规划问题。其步骤是 :
(1) 对含有某参变量 t 的参数线性规划问题。先令 t= 0,用单纯形法求出最优解; (2) 用灵敏度分析法,将参变量 t直接反映到最终表中;
(3 ) 当参变量 t 连续变大或变小时 , 观察 b 列和检验数行各数字的变化。若在 b 列首先出现某负值时 , 则以它对应的变量为换出变量 ; 于是用对偶单纯形法迭代一步。若在检 验数行首先出现某正值时 , 则将它对应的变量为换入变量 ; 用单纯形法迭代一步 ;
(4) 在经迭代一步后得到的新表上,令参变量 t 继续变大或变小,重复步骤(3),直到 b 列不能再出现负值 , 检验数行不能再出现正值为止。
其实,关于灵敏度分析,理解即可,一般LP问题的商用软件,都有提供分析工具。