python实现矢量积、叉积、外积、张量积
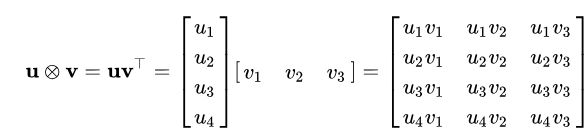
张量积 一般指的是Kronecker product a⊗b
很显然，该运算不遵守交换律。
import numpy as np
a = np.eye(3)
b = np.ones((3,2,3))
c = np.kron(a,b)a
array([[ 1., 0., 0.],
[ 0., 1., 0.],
[ 0., 0., 1.]])
b
array([[[ 1., 1., 1.],
[ 1., 1., 1.]],
[[ 1., 1., 1.],
[ 1., 1., 1.]],
[[ 1., 1., 1.],
[ 1., 1., 1.]]])
c
array([[[ 1., 1., 1., 0., 0., 0., 0., 0., 0.],
[ 1., 1., 1., 0., 0., 0., 0., 0., 0.],
[ 0., 0., 0., 1., 1., 1., 0., 0., 0.],
[ 0., 0., 0., 1., 1., 1., 0., 0., 0.],
[ 0., 0., 0., 0., 0., 0., 1., 1., 1.],
[ 0., 0., 0., 0., 0., 0., 1., 1., 1.]],
[[ 1., 1., 1., 0., 0., 0., 0., 0., 0.],
[ 1., 1., 1., 0., 0., 0., 0., 0., 0.],
[ 0., 0., 0., 1., 1., 1., 0., 0., 0.],
[ 0., 0., 0., 1., 1., 1., 0., 0., 0.],
[ 0., 0., 0., 0., 0., 0., 1., 1., 1.],
[ 0., 0., 0., 0., 0., 0., 1., 1., 1.]],
[[ 1., 1., 1., 0., 0., 0., 0., 0., 0.],
[ 1., 1., 1., 0., 0., 0., 0., 0., 0.],
[ 0., 0., 0., 1., 1., 1., 0., 0., 0.],
[ 0., 0., 0., 1., 1., 1., 0., 0., 0.],
[ 0., 0., 0., 0., 0., 0., 1., 1., 1.],
[ 0., 0., 0., 0., 0., 0., 1., 1., 1.]]])
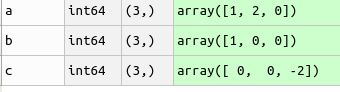
叉积 cross product，一般是两个向量之间的计算，得到一个垂直这两个向量的向量。向量必须是3维，2维向量则广播成3维（注意这里向量维不是空间维）。如果是矩阵，则是矩阵的行向量或列向量之间的运算。
import numpy as np
a = np.array([1,2,0])
b = np.array([1,0,0])
c = np.cross(a,b)
外积是Kronecker product的一种特殊形式，是两个一维向量之间的运算。
import numpy as np
a = np.array([1,2,3,4])
b = np.ones([3,1])
c = np.outer(a,b)
d = np.kron(a,b)c
array([[ 1., 1., 1.],
[ 2., 2., 2.],
[ 3., 3., 3.],
[ 4., 4., 4.]])
d
array([[ 1., 2., 3., 4.],
[ 1., 2., 3., 4.],
[ 1., 2., 3., 4.]])
如果b改成1×3，那么该例d为1×12：
array([[ 1., 1., 1., 2., 2., 2., 3., 3., 3., 4., 4., 4.]])
内积没什么好说的，大家最熟悉了。
最后提一下，python(numpy)的矩阵元素相乘（elementwise）只有numpy.multiply()和*。其他np.dot()，np.matmul()均是矩阵乘。
Hadamard product (also known as the Schur product）
