粒子滤波与重要性采样

最近又复习粒子滤波，感觉实际代码和推导总是有那么一些差距那一理解，主要是好好的分布为什么一转就变成特征似然程度了。这个东西让我们理一遍

之前理解粒子的思想可能是有一些问题的，对于一个未知分布来说的话，我们想要知道这个分布的期望，好，现在我们均匀的去撒粒子吧，其实蒙特卡洛方法来说，我们只要对大量的粒子求平均就可以知道我们想要分布的期望了。但是在粒子滤波的问题里面，我们偏偏对每一个粒子反馈的情报加上了一个权，这个权代表我们-是不是很信任这个分布。再看这个权的分布形式，实际上就是它和目标的相似程度。现在我们明白了，粒子滤波的结构实际上是加了一层重要性采样的思想在里面的蒙特卡洛方法。

现在我们要解决的就是如何估计这个相似程度的问题。粒子滤波在这里做了很牛逼的一件事。我们不知道这个东西原本的分布是什么，，但是我们可以观察某一个特征啊，如果这个特征的分布能够代表原来的分布的话，我们是不是可以近似这样来理解！！！！！！！

让我们一步一步理解这个思路：
蒙特卡洛方法是什么，就是试验，用大量的样本去替代概率。
比如说，我们想要知道一个骰子投出点数的期望，我们就不断去投这个骰子，把每一次的结果平均取来，就可以知道这个筛子的期望了。
在这个过程之中，有一个非常重要的点：为什么我们通过简单的平均就能够推算出这个骰子的期望呢？原因在于每一次单独实验的概率分布都是符合骰子本来的概率分布的。对于蒙特卡洛方法来说，样本的分布和要求取期望的分布一致至关重要。

蒙特卡洛方法应用的另一个常用的例子是使用计算面积。
就是这个玩意：

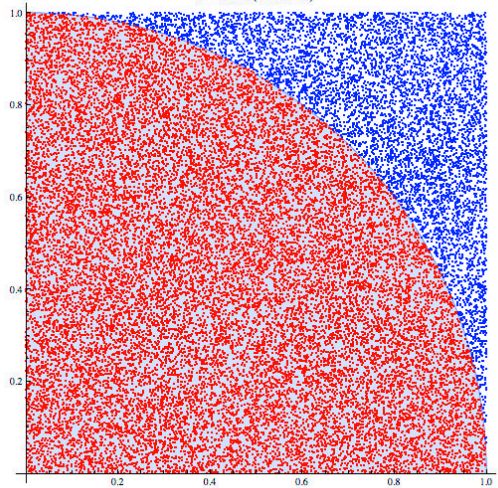
我们用维基百科蒙特卡洛方法词条的这个图来说明。如果我想要知道这个四分之一圆的面积，一种方法当然是测量半径，然后用圆面积公式 4πr2 来算。但是假设我们回到古代，并不知道 π 的具体数值。就没有办法算圆的面积了么？这时候我们可以用蒙特卡洛方法解决，在一个矩形空间均匀撒下粒子，然后计算落在圆面积里面的粒子和撒下所有粒子的比值，这个比值刚好就是圆面积和这个矩形空间面积的比值。于是，圆的面积就可以被反推回来了。
这个例子实际上是由一定误导性的，原因在于：这不是最朴素的蒙特卡洛方法！！为什么呢？试问：每一个粒子遵从的是什么分布？为了让求值正确，我们投放粒子的时候是在整个空间均匀分布的。但是，属于圆的部分在这个矩形空间并非是均匀分布的。换而言之，这两个分布，不一样啊，那还算什么蒙特卡洛方法呢。那么这套算法究竟是经历了什么，让它又歪打正着算出正确的结果了呢，这就是我们要重点讨论的问题：重要性采样。

在此之前，我们还需要绕个圈子，好更好的引出我们的问题。蒙特卡洛方法其实核心就在于解决一个分布的期望问题，而且，这个分布的概率分布还他妈必须是已知的！（或者你能够确信我们的样本一定一定是和要求期望的分布时一致的）
比如，一个变量 x 的概率分布是 p(x) ，我们要求它的期望怎么求？按照定义

E(x)=∫xp(x)dx

很好，现在我告诉你，这个 p(x) 形式巨复杂巨难算，臣妾根本积不出来（在高维的情况下尤甚）。那好，我就们不得不祭出蒙特卡洛了，蒙特卡洛告诉你，想知道期望，按照这个分布得到一些样本，平均就好了嘛。问题又来了，我们该怎么按照这个分布生成样本呢。
比如，我们想要按照正态分布生成一些样本，继而通过这些样本获取它的期望。但是，就计算机的角度来说，我们只能够得到均匀分布的随机数如何从均匀分布的随机数得到高斯分布的随机数呢？概率累计！

这里我们使用：http://blog.csdn.net/tudouniurou/article/details/6277526 的一个例子
例如我想按照标准正态分布N(0,1)取10个随机数，那么我首先在[0,1]上按照均匀分布取10个点

0.4505 0.0838 0.2290 0.9133 0.1524 0.8258 0.5383 0.9961 0.0782 0.4427

然后，我去找这些值在cdf上对应的x0，如下

-0.1243 -1.3798 -0.7422 1.3616 -1.0263 0.9378 0.0963 2.6636 -1.4175 -0.1442

用画图来表述的话，是这样的：

可是问题在这里：本来这个分布我就积不出来，你还要我积分，有啥用呢。重点来了！积不出来，我可以试着用其他方法啊，让我们改变一下求期望积分的形式：

E(x)=∫xp(x)q(x)q(x)dx

对，我们把这个积分项目上下乘以了一个q(x)，这是我们已知的一个分布，并且这个分布在数学上来说是可以随意设定的。那么，这个式子其实可以理解为：现在我们求取的是 xp(x)q(x) 的期望，这个变量是按照 q(x) 分布的。看不太明白？让我们来看一个例子，这个例子出自
Udacity的机器人人工智能教程-CS373 Artificial Intelligence for Robotics Programming a Robotic Car：

绿色的点是一个机器人，看色的线代表激光发出的测量线，现在它被随机放在了地图的一个位置，它想要知道自己到底在哪里，于是，它就开始猜测：由于没有任何的先验信息，所以一开始，它可能存在与房间的任何一个角落，每一个红色的点即代表机器人对自己所处位置的一个猜想，这就是我们在蒙特卡洛方法里面所提到的样本。而猜测（红色点）的分布是均匀的，也就是之前式子里面的 q(x) 分布。当然，每一个猜测有好有坏，不然我们简单的把所有粒子一平均，机器人对自己位置的猜想肯定一直会处于整个房间的最中心了。 p(x)q(x) 这部分我们称之为权值，就是为了衡量每个猜测的好坏，也就是衡量我们随意决定的分布和真实分布之间的相似度。
在这里其实还有一个小问题的，我们应该如何去衡量 p(x)q(x) ，在机器人定位问题里面， p(x) 我们根本不知道！不知道的东西怎么去衡量啊，粒子滤波在这里有很牛逼的一招：这个不知道，我们可以抓特征啊。在这个问题里面，由于机器人知道整个房间的地图，又能探测到自己周边环境的样子，所以它可以把 p(x)q(x) 转换为计算当前猜测点的特和探测器感知的周围环境的似然程度！粒子滤波器牛逼的地方就在这里：我不知道真实情况怎么分布的，但是我可以追踪你的一个特征，并且我假设：这个特征的分布期望和原始目标的分布期望是一致的。这就好像是老师叫你去操场上找人，但是你并不知道要找的人会在操场哪里出现，而且最关键的是你还不认识那个人。这时候老师说，不知道不认识不要紧，你只要找那个穿着红衣服的人就可以了。然后你就去操场一看，哟，红衣服在这里，虽然你不认识他，但是你认为红衣服是他在这个状态空间的唯一特征，所以你还是准确找到了这个人。
这样， p(x)q(x) 在实际计算中实际上就近似于计算特征的相似程度了。在这个问题里面，就是比较猜测位置姿态所应该得到的环境信息和实际得到的环境信息之间的差异。
当然，为了更好的性能，我们还是希望 p(x)q(x) 尽可能接近于1，也就是 q(x) 尽可能接近于原始 p(x) 的分布的，这个问题我们可以通过粒子重采样解决。在这里我们不深入讨论，只给出重采样迭代之后的效果：






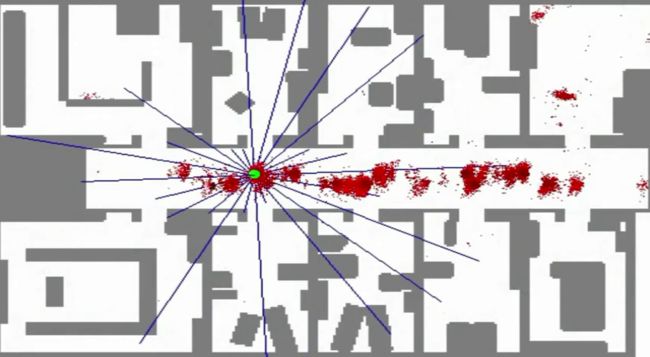
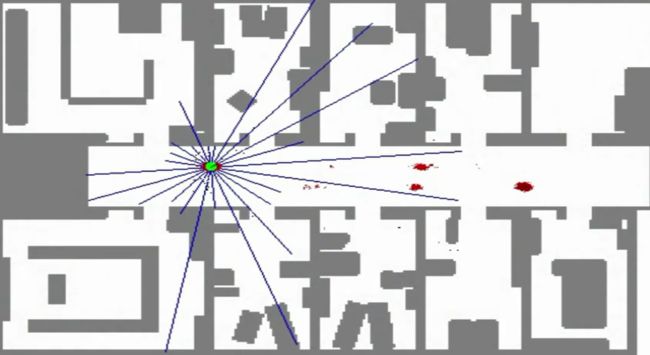
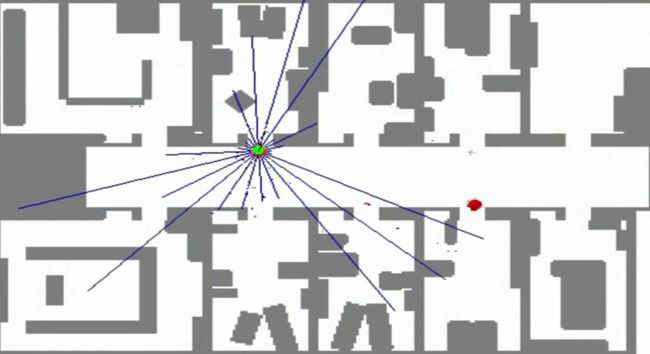
可以看到，在移动过程中，机器人的猜测渐渐全部收敛到机器人的真实位置了！
真他妈好玩。

最后回到之前我们提到的算面积那个问题，它实际上也是采用了重要性采样的思想，而权重分布变成了0-1分布，所以得到了之前的结果。
均匀的撒粒子只是一种折中的方法。在不知道原始分布是什么样子的情况下，均匀分布的粒子最具有适应性，为了提升性能，我们在做重采样的时候，依然会不断优化粒子，使其趋近于原来的概率分布。这样使其不断接近真实分布，从而完成整个蒙特卡洛的思路。