基于Theano的多层神经网络及其实现(一)

前言

本文讨论了多层神经网络中的优化技巧及其theano实现，以theano官网中关于多层神经网络的教程为蓝本，并补充作者对于优化算法的理解，是对多层神经网络及其优化技巧相关资料进行的一次整合和报告。

1.Theano简介

Theano是一个允许用户定义、优化并且评价数学表达式的python函数库，其在多维变量的情况下依然可以保持很高的效率和处理能力。基于cupy的GPU拓展使其拥有在GPU上并行处理算式的能力，使训练时间大大降低。
Theano的安装请参阅：http://www.deeplearning.net/software/theano/install.html#install。
Theano的GPU加速部分请参阅：http://www.deeplearning.net/software/theano/library/config.html#libdoc-config 对theanoConfig文件进行调整
我们使用了Theano作为多层神经网络代码实现的一个基础，主要是因为其对于网络架构的清晰表达能力以及强大的λ演算所带来的易于理解的函数推导关系。比如，在一个普通的优化问题中，我们的优化目标是这样一个函数：

f(x)=x2+2x+1+ex

在朴素的求解过程中，我们需要得到这个函数形式的导数：

f′(x)=2x+2+ex

之后按照梯度下降法则，从初始的搜索点 x0 开始，有：

xn+1=xn−ηf′(x)

在theano中 ，这一流程可以转化为如下代码：

# -*- coding: UTF-8 -*-
import theano
#定义变量
x = theano.tensor.dscalar('x')
#定义输出表达式 x^2+2x+1
y = x**2+2*x+1+theano.tensor.exp(x)
#定义梯度--此过程将自动推演出梯度表达式
gy = theano.tensor.grad(y,x)
#定义迭代公式 迭代步长为0.01
f = theano.function(inputs=[x],outputs=[y,gy],updates=(x-0.01*gy))
#开始迭代,优化直到梯度接近0
grad = 999
while grad>0.0001:
    out, grad = f(0)

因此，使用者不必纠结于复杂的推导以及数学演算之间的关系，只需要确定目标函数以及迭代方法，theano自带的λ演算会计算出相应的表达式，从而让使用者能够更加专心应对目标函数的设计等方面的问题。也正是因为其在公式推演方面的优越性，我们才选择Theano而非更普遍的caffe作为示例程序库。这样更有利于理解优化算法及其推导意义。

2.多层神经网络

多层神经网络起源于罗森布拉特感知机（即有名的感知机算法），其由神经元的生物结构启发，提出决策是由不同感知结点的受激程度加权求和得出，其数学表达式为：

f(x)=∑k=0nσk∗xk

其中 xk 为第 k 个感受单元所感受到的数值， σk 为第 k 个感受单元的权值， f(x) 为输出。
但是朴素的罗森布拉特感知机无法分割XOR（异或）问题。基于kernal技巧等思路的启发，人们开始尝试使用多层的感知机构筑多层神经网络，尝试在较高的VC维进行分割，其相较于朴素的罗森布拉特感知机不仅克服了XOR问题的困局，还有这如下优点：

• 高度的并行性
  神经网络的每一个单元在每一层互相不影响（玻尔兹曼机等除外），非常利于GPU等实现并行化计算。其训练过程也可以应用其单元之间不互相连接的优势将每个单元的训练分为各个线程进行处理。可以有效提升计算速度，在实际测试中，并行化计算的时间效率比起普通计算模式可提升7倍以上的效率。
• 强大的表示能力
  根据[1]指出，三层以上的神经网络只要其拥有足够数目的结点，就可以拥有表达任何形式函数的能力。诚然在现在看来，如何确定结点数目仍然是一个世界性的难题。在通常的训练流程中一般使用试错法来改变结点数目及其分类性能。但是在结点数目足够多的时候，其具有描述任何非线性函数的能力，这一点是十分令人振奋和惊异的。
• 强大的适应性
  由于整个网络的表示只由各个结点之间的权值决定（现在也有研究如何在训练过程中改变网络结构得到最好的优化，我们在这里只讨论传统神经网络的结构），整个网络在需要添加输出类别，添加输入样本等操作的时候会显得十分便捷。增加的类别并不会影响之前类别的输出。

现在流行的深度学习算法，在其朴素意义上来说，也正是结点数目极多，层次数目极深的神经网络的一种实现。而且随着计算机处理能力和大数据方法逐渐完善，其表达能力和计算效率势必会得到新的提升。研究神经网络相当于是深度学习的一个入门级体验，这也是我们在本文中介绍神经网络及其优化算法的目的。

3.多层神经网络的优化算法

多层神经网络在直观上理解就是单层神经网络加入多个隐层所得到的网络。从kernal的角度来理解，每个隐层都是从N维空间的M维空间的一个映射，其也可以理解为将其映射到高VC维的一个kernal，隐层的的输出将作为输出层（或下一个隐层）的输入。其每一层结构和单层神经网络没有区别，都是N维输入的线性加权与sigmiod函数等激活函数的组合。在一些高层的神经网络中可能还会采取“skip”的策略，即本层神经元并不只与上一层的神经元相连，其可能还与更低级层的神经元相连。在本文我们只讨论传统意义上的多层神经网络，即以多个单层神经网络层叠链接而成的网络结构。
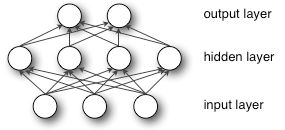
以三层神经网络为例，其结构如图所示：

其输出函数为：

out(x)=g(b+W∗f(c+Vx))

其中 b，c 为输出层与输入层的偏置量，其在多层神经网络中被证明与该神经层的敏感程度相关， W，V 为输出层与输入层的线性加权系数，在多输入多输出的网络结构中，其为一个 M×N 的矩阵，其中 M 为输出维度， N 为输入维度。 g(),f() 为输出函数，是为了标签化程序的输出而设计的（比如在二分类问题中，需要把程序输出映射到0和1两个值上）。输出函数一般采用sigmoid函数或者tanh函数，在一般实践中，往往认为tanh函数较之sigmoid函数更容易收敛且得到更好的结果。现在深度学习的研究中，又提出ReLu等非平滑曲线作为激活函数，并取得了较好的效果。

3.1优化目标

在监督学习的训练架构中，每一个样本的输入都是存在一个样本标签来校验其分类结果是否正确的。这样，就可以通过网络经过激活函数的输出与样本标签的差作为优化目标进行优化。
最终其目标都是通过系数优化求取损失函数的最小值，即：

b,c,W,V=argminb,c,W,vL(x,y)

从这个式子可以看出，在没有任何先验条件的情况下，这个式子的优化是一个NP难问题，这样的问题在如此高维度是非常难以求解的，但是，我们可以通过使用一系列的样本训练整个网络的方法使得优化过程有迹可循。
我们可以先定义样本集合 X 及其对应的标签集合 Y ,每一个样本对可以表示为 x,y，y 为其对应的样本标签。定义其与样本标签的平方误差为累加损失。
这样，我们就得到了损失函数：

L(x,y)=||out(x)−y||2=∑i(out(x)−y)2

在这里，我们使用的是平方误差作为优化目标，其可以从目标噪声为高斯分布的模型中推导而出。在噪声假设为其他不同分布时，也可以使用其他范数作为优化目标。比如基于稀疏规范的L1损失函数:

L(x,y)=||out(x)−y||21=∑i|(out(x)−y)|

为了预防过拟合，损失函数可以可以人为加入不通过的约束规范来限制系数的稀疏性质，比如加入了稀疏规范的均方误差损失函数：

L(x,y)=||out(x)−y||2+||W,V||0=∑i(out(x)−y)2+||W,V||0

3.2前向误差传播算法

多层神经网络的优化思路和单层神经网络类似，都是通过优化损失函数中的系数取得优化效果。但是，因为存在多个层数的原因，无法将系数进行一次性的全部优化，所以主要采用分层优化，误差由输出层向输入层渐渐传播的策略进行。只是由于只有输出层可以得知其系数与优化目标的关系，所以每一层的优化步骤都必须依赖于输出层，即将输出层的误差层层反向传播回优化层。约定： hi 为神经网络的第 i 层，且 h0 为输入层， hk−1 为输出层(整个网络一共k层)。 wi,j 为第i层的第j个线性系数， bi 为第i层的偏置。则其优化策略为：

for i=k down to 1
    从输出层链式求导至该层 
    对该层进行优化
if 模型稳定
    退出优化
else
    继续

3.3前向误差传播在三层神经网络中的推导

现在我们使用一个激活函数为 f(x) 的三层神经网络推导。另定义 xi yi 分别为第i层的输入和输出
则有：对于隐层，其对于误差函数的梯度为：

∂L∂wji=∂L∂yji∂yji∂xji−1∂xji−1∂wji

当损失函数选取为sigmiod函数时候，其有着一个优秀的性质：

sigmiod′=sigmiod(1−sigmoid)

假定损失函数为均方误差，所以我们有：

gradhidden=2(y−ytrue)y(1−y)wji

这样就得到了隐层函数的更新公式，对于输入节点，使用链式求导法则，同样的：

∂L∂wji=∂L∂yji∂yji∂yji−1∂yji−1∂xji−1∂xji−1∂wji

求得:

gradinput=xi−1yn−1(1−yn−1)∑k=0nwkigeadhidden

再按照上一节所描述优化方法优化即可。