最小堆实现哈夫曼树的构造及哈夫曼编码、解码
以下程序的算法思想主要来自于浙江大学陈越老师主编的数据结构一书。最大堆(最小堆思想差不多)这里就不再多说,这里主要讲讲哈夫曼树的定义及实现。
Huffman Tree
相关概念:
结点的路径长度:从根结点到该结点的路径上分支的数目。
树的路径长度:树中每个结点的路径长度之和。(从树根到其余各结点的路径长度之和)
结点的带权路径长度(WPL):结点的路径长度与该结点所带权值的乘积。
树的带权路径长度:树中所有叶子结点的带权路径长度之和。
设一棵树有n个叶子结点,每个叶结点带有权值wk,结点的路径长度为lk,则树的带权路径长度可以表示为:
![]()
哈夫曼树的定义: 假设有n个权值,构造有n个叶子结点的二叉树,每个叶子结点的权值是n个权值之一,这样的二叉树可以构造很多棵,其中必有一棵是带权路径长度最小的,这棵二叉树就称为最优二叉树或哈夫曼树。
构造Huffman树的步骤:
(1) 根据给定的n个权值,构造n棵只有一个根结点的二叉树,n个权值分别是这些二叉树根结点的权;
(2) 设F是由这n棵二叉树构成的集合,在F中选取两棵根结点权值最小的树作为左、右子树,构造成一颗新的二叉树,置新二叉树根结点的权值等于左、右子树根结点的权值之和。为了使得到的哈夫曼树的结构唯一,规定根结点权值最小的作为新二叉树的左子树;
(3) 从F中删除(2)中作为左、右子树的两棵二叉树,并将新构造的二叉树加入到集合F中;
(4) 重复(2)、(3)步,直到F中只含一棵二叉树为止,这棵二叉树便是要建立的哈夫曼树。
说明:n个结点需要进行n-1次合并,每次合并都产生一个新的结点,最终的Huffman树共有2n-1个结点。
为了便于抽取最小权值的子树,在树的构造过程中使用了最小堆及其插入,删除等操作。这里堆中的元素是一个加了权值的树结点的指针。
说了这么多,也该实现代码了。100好几十行的代码撸下来,感觉自己神清气爽,等等...,编译没毛病,运行。。。呃呃呃,什么!!!我就输入了一个整数(表示接下来我要输入多少个权值),程序就跟我说拜拜了!!!于是我就只能进入搬砖工Debug模式了。。。调试程序嘛,当然要一步步来,首先当然是调试主程序里的第一个函数(CreateMinHeap(2*N)),我就在这个函数前后写了一句printf("ok\n"),一运行,,,O no,只有一个ok,当然这个函数有毛病,于是我进去这个函数定义里面一看,这老哥没毛病啊,左看右看,找不出来。。。想了老久,只好启动码农搬救兵(大佬-杰)模式,什么!!!你也看不出来???苍天啊,我的内心其实还有点【小窃喜】,救兵也没看出来,说明我这个问题不是一般的问题,我自己没看出来也还ok。我的肚子这时候又出来加速我的放弃了,于是我就打算吃饭,打道回府。。。
故事到这里难道就结束了吗?no no no。在去食堂的路上,我想着作为一名党神圣的搬砖工,不能就这么放弃了啊,不然将来怎么建设党的伟大事业。我就在路上想啊想啊,越想越得劲,感觉思路越来越清晰,到了食堂打完饭一坐下,没吃几口饭,猛一拍大腿【卧槽】,想出来了。。。当时恨不得当场把电脑掏出来调试一波【别人会不会把我当傻子。。。】。主要问题是我在动态申请一个指针数组的时候给这个指针数组分配的内存空间(这时候指针数组的元素可能是空指针,或者不知道指向一个什么地方),我却在后面直接使用了这个指针指向的对象(结构体)里面的元素,这样肯定不行啊!!!比如说你指向了一片虚无的空间或者是指向一个不知道是什么地方,然后对另一个人说,这个地方有好多妹子,快去撩妹吧,撩你个大头鬼哦,你个糟老头子坏得很~,没给我地址怎么找这个地方!!!你要是指着女生宿舍说这个还差不多(不过咱们也不能真进去女生宿舍啊,进去了也别说是我教唆的【哈哈】)。于是我只好先一个个申请一个地址空间,再把他们赋值给这个指针数组就行了。(这里告诉我们一个道理,当你调不出代码的时候,出去吃个饭,或者散散步说不定就想出来了,大脑持续高负荷工作也是会累的)
修改好之后运行程序没毛病,再也不会没执行完就崩溃了,说明程序大体上没什么毛病(诸如溢出、指针指向不明),只不过算法上的实现是需要程序员自己检查的。
你们以为这就结束了吗?那你们也太小看程序员为什么高薪了(那是因为他们总写出满带bug的程序,然后他们成天到晚Debug,累得不行【过头了,过头了】),然后有人问,那直接写出没bug的程序呗,说的轻巧,大可一试,小程序倒还好,那种成百上千行的代码难道能完全没问题吗?哈哈,偏题了,偏题了。接下来这个问题是我也不曾想过会出现的,当然因为程序运行结果不对,我只好对写的函数一个个在主函数里面进行分别实现,当然,你很容易看出没问题的函数就没必要了。最后,终于定位在了哈夫曼构造函数这个函数里面(因为其他函数都没问题),但我非常不解啊,因为这个函数是教科书上有的,我原封不动的抄下来的,不应该有问题啊(函数算法我也理解的差不多),我找啊找,各种Debug模式开启,终于发现for循环里的判决条件有问题!!!(下面程序中也标记了)for循坏里面的操作会改变判决条件,【卧槽】,这可不行啊,于是做了一个小小修改就完美解决了。(这件事告诉我们一个道理,即使是书本上的知识,也是会有毛病的。。。)修改之后,编译、运行、程序结果终于出来了。。。
#include
#include
typedef struct TreeNode *HuffmanTree;
typedef struct TreeNode{
int Weight; //权值
HuffmanTree Left;
HuffmanTree Right;
}HuffmanNode;
#define MinData -1 //随着堆元素的具体值而改变
typedef struct HeapStruct *MinHeap;
struct HeapStruct{
HuffmanTree *data; //存储堆元素的数组 存储时从下标1开始
int Size; //堆的当前元素的个数
int Capacity; //堆的最大容量
};
HuffmanTree NewHuffmanNode();
MinHeap CreateMinHeap(int MaxSize);
bool Insert(MinHeap H,HuffmanTree item);
HuffmanTree DeleteMin(MinHeap H);
MinHeap BuildMinHeap(MinHeap H);
HuffmanTree Huffman(MinHeap H);
void PreOrderTraversal(HuffmanTree BST);
int main()
{
int i,N;
MinHeap h;
HuffmanTree T,BT = NULL;
printf("请输入叶子结点的个数:\n");
scanf("%d",&N);
h = CreateMinHeap(2*N); //创建最小堆
printf("请输入%d个叶子结点对应的权值:\n",N);
for(i=1; i<=N; i++){/*最小堆元素赋值*/
T = NewHuffmanNode();
scanf("%d",&(T->Weight));
h->data[++(h->Size)] = T;
}
BT = Huffman(h); //构造哈夫曼树
printf("先序遍历此哈夫曼树的权值:\n");
PreOrderTraversal(BT); //先序遍历此哈夫曼树
return 0;
}
/*哈夫曼树构造算法*/
HuffmanTree Huffman(MinHeap H)
{/*假设H->Size个权值已经存在H->data[]->Weight里*/
int i,num;
HuffmanTree T;
BuildMinHeap( H ); //将H->data[]按权值调整为最小堆
/*此处必须将H->Size的值交给num,因为后面做DeleteMin()和 Insert()函数会改变H->Size的值*/
num = H->Size;
for(i=1; iSize-1次合并 //此处教科书有问题!原书直接为H->Size
T = NewHuffmanNode(); //建立一个新的根结点
T->Left = DeleteMin(H); //从最小堆中删除一个节点,作为新T的左子结点
T->Right = DeleteMin(H); //从最小堆中删除一个节点,作为新T的右子结点
T->Weight = T->Left->Weight+T->Right->Weight; //计算新权值
//printf("%3d 0x%x 0x%x\n",T->Weight,T->Left,T->Right);
Insert(H,T); //将新T插入到最小堆
}
T = DeleteMin(H);
return T;
}
/*****先序遍历*****/
void PreOrderTraversal(HuffmanTree BST)
{
if( BST ){
printf("%d ",BST->Weight); //先访问根节点
PreOrderTraversal(BST->Left); //再访问左子树
PreOrderTraversal(BST->Right); //最后访问右子树
}
}
HuffmanTree NewHuffmanNode()
{
HuffmanTree BST = (HuffmanTree)malloc(sizeof(HuffmanNode));
BST->Weight = 0;
BST->Left = BST->Right = NULL;
return BST;
}
MinHeap CreateMinHeap(int MaxSize)
{ /*创建容量为MaxSize的最小堆*/
MinHeap H = (MinHeap)malloc(sizeof(struct HeapStruct));
H->data = (HuffmanTree *)malloc((MaxSize+1) * sizeof(HuffmanTree));
H->Size = 0;
H->Capacity = MaxSize;
HuffmanTree T = NewHuffmanNode();
T->Weight = MinData; /*定义哨兵-为小于堆中所有可能元素权值的值,便于以后更快操作*/
H->data[0] = T;
return H;
}
bool IsFull(MinHeap H)
{
return (H->Size == H->Capacity);
}
bool IsEmpty(MinHeap H)
{
return (H->Size == 0);
}
/*插入算法-将新增结点插入到从其父结点到根结点的有序序列中*/
bool Insert(MinHeap H,HuffmanTree item)
{/*将元素item插入到最小堆H中,其中H->data[0]已被定义为哨兵*/
int i;
if( IsFull(H) ){
printf("最小堆已满\n");
return false;
}
i = ++H->Size; //i指向插入后堆中的最后一个元素的位置
for(; H->data[i/2]->Weight > item->Weight; i/=2) //无哨兵,则增加判决条件 i>1
H->data[i] = H->data[i/2]; //向下过滤结点
H->data[i] = item; //将item插入
return true;
}
HuffmanTree DeleteMin(MinHeap H)
{/*从最小堆H中取出权值为最小的元素,并删除一个结点*/
int parent,child;
HuffmanTree MinItem,temp = NULL;
if( IsEmpty(H) ){
printf("最小堆为空\n");
return NULL;
}
MinItem = H->data[1]; //取出根结点-最小的元素-记录下来
/*用最小堆中的最后一个元素从根结点开始向上过滤下层结点*/
temp = H->data[H->Size--]; //最小堆中最后一个元素,暂时将其视为放在了根结点
for(parent=1; parent*2<=H->Size; parent=child){
child = parent*2;
if((child != H->Size) && (H->data[child]->Weight > H->data[child+1]->Weight)){/*有右儿子,并且左儿子权值大于右儿子*/
child++; //child指向左右儿子中较小者
}
if(temp->Weight > H->data[child]->Weight){
H->data[parent] = H->data[child]; //向上过滤结点-temp存放位置下移到child位置
}else{
break; //找到了合适的位置
}
}
H->data[parent] = temp; //temp存放到此处
return MinItem;
}
MinHeap BuildMinHeap(MinHeap H)
{/*这里假设所有的H->Size个元素已经存在H->data[]中*/
/*本函数将H->data[]中的元素调整,使其满足堆的有序性*/
int i,parent,child;
HuffmanTree temp;
for(i=H->Size/2;i>0;i--){ //从最后一个父结点开始,直到根结点
temp = H->data[i];
for(parent=i; parent*2<=H->Size; parent=child){
/*向下过滤*/
child = parent*2;
if((child != H->Size) && (H->data[child]->Weight > H->data[child+1]->Weight)){/*有右儿子,并且左儿子权值大于右儿子*/
child++; //child指向左右儿子中较小者
}
if(temp->Weight > H->data[child]->Weight){
H->data[parent] = H->data[child]; //向上过滤结点-temp存放位置下移到child位置
}else{
break; //找到了合适的位置
}
}/*结束内部for循环对以H->data[i]为根的子树的调整*/
H->data[parent] = temp; //temp(原H->data[i])存放到此处
}
return H;
}
运行结果为:
哈夫曼编码解码
哈夫曼树构造完成以后,哈夫曼编码就很容易完成了。我们只要把哈夫曼树每个结点的左分支标记为0,右分支标记为1,某一字符(权值)的编码可通过组合从根结点到该字符结点(叶结点)的路径上所标记的0,1得到。解码的话我们只要根据编码序列从根结点开始出发,0则想左子树走,1则向右子树走,直到走到一个叶子结点出,就可输出此叶子结点的字符值;每输出一个叶子结点,就从根结点从新开始走。具体如下图所示:
因为每个叶子结点的权值可能一样,为了区分、并且我们接下来要对字符进行 编解码,所以我们给树结点结构在加入一个字符元素。如下:
typedef struct TreeNode *HuffmanTree;
typedef struct TreeNode{
char ch; //要编码的字符
int Weight; //权值
HuffmanTree Left;
HuffmanTree Right;
}HuffmanNode;具体的编解码算法如下:
/************递归进行哈夫曼编码*************/
void HuffmanCode(HuffmanTree BST,int depth) //depth为目前编码到哈夫曼树的深度(层次)
{
static int code[10]; //编码空间
if( BST ){
if( (BST->Left == NULL) && (BST->Right == NULL)){ //找到了叶结点
printf("字符%c对应权值为%d的哈夫曼编码为:",BST->ch,BST->Weight);
for(int i=0; iLeft,depth+1);
code[depth] = 1; //往右子树方向编码为1
HuffmanCode(BST->Right,depth+1);
}
}
}
/*******************哈夫曼解码*********************/
void HuffmanDecode(char ch[],HuffmanTree BST) //ch[] 要解码的序列
{
int cnt;
int num[100];
HuffmanTree temp;
for(int i=0; iLeft != NULL ) && (temp->Right != NULL)){
if(num[cnt] == 0){
temp = temp->Left;
}else{
temp = temp->Right;
}
cnt++;
}
printf("%c",temp->ch); //输出解码后对应结点的字符
}
}
}
将这两个函数放入到主程序里面,可以得到:
#include
#include
#include
typedef struct TreeNode *HuffmanTree;
typedef struct TreeNode{
char ch; //要编码的字符
int Weight; //权值
HuffmanTree Left;
HuffmanTree Right;
}HuffmanNode;
#define MinData -10 //随着堆元素的具体值而改变
typedef struct HeapStruct *MinHeap;
struct HeapStruct{
HuffmanTree *data; //存储堆元素的数组 存储时从下标1开始
int Size; //堆的当前元素的个数
int Capacity; //堆的最大容量
};
HuffmanTree NewHuffmanNode();
MinHeap CreateMinHeap(int MaxSize);
bool Insert(MinHeap H,HuffmanTree item);
HuffmanTree DeleteMin(MinHeap H);
MinHeap BuildMinHeap(MinHeap H);
HuffmanTree Huffman(MinHeap H);
void PreOrderTraversal(HuffmanTree BST);
void HuffmanCode(HuffmanTree BST,int depth);
void HuffmanDecode(char ch[],HuffmanTree BST);
int main()
{
int i,N;
MinHeap h;
HuffmanTree T,BT = NULL;
printf("请输入叶子结点的个数:\n");
scanf("%d",&N);
h = CreateMinHeap(2*N); //创建最小堆 //N个叶子节点最终形成的哈夫曼树最多有2N-1个树结点
printf("请输入%d个叶子结点对应的权值:\n",N);
for(i=1; i<=N; i++){/*最小堆元素赋值*/
T = NewHuffmanNode();
scanf("%d",&(T->Weight));
//scanf("%d-%c",&(T->Weight),&(T->ch));
h->data[++(h->Size)] = T;
}
char string[100];
printf("请连续输入这%d个叶子结点各自代表的字符:\n",N);
getchar(); //吸收上面的换行符
gets(string);
for(i=1; i<=h->Size; i++){/*最小堆元素赋值*/
h->data[i]->ch= string[i-1];
}
BT = Huffman(h); //构造哈夫曼树
printf("先序遍历此哈夫曼树的权值:\n");
PreOrderTraversal(BT); //先序遍历此哈夫曼树
printf("\n");
HuffmanCode(BT,0);
printf("要解码吗?请输入二进制编码序列:\n");
char ch[100];
gets(ch);
printf("解码结果为:\n");
HuffmanDecode(ch,BT);
return 0;
}
/*哈夫曼树构造算法*/
HuffmanTree Huffman(MinHeap H)
{/*假设H->Size个权值已经存在H->data[]->Weight里*/
int i,num;
HuffmanTree T;
BuildMinHeap( H ); //将H->data[]按权值调整为最小堆
/*此处必须将H->Size的值交给num,因为后面做DeleteMin()和 Insert()函数会改变H->Size的值*/
num = H->Size;
for(i=1; iSize-1次合并 //此处教科书有问题!
T = NewHuffmanNode(); //建立一个新的根结点
T->Left = DeleteMin(H); //从最小堆中删除一个节点,作为新T的左子结点
T->Right = DeleteMin(H); //从最小堆中删除一个节点,作为新T的右子结点
T->Weight = T->Left->Weight+T->Right->Weight; //计算新权值
// printf("%3d 0x%x 0x%x\n",T->Weight,T->Left,T->Right);
Insert(H,T); //将新T插入到最小堆
}
T = DeleteMin(H);
return T;
}
/************递归进行哈夫曼编码*************/
void HuffmanCode(HuffmanTree BST,int depth) //depth为目前编码到哈夫曼树的深度(层次)
{
static int code[10]; //编码空间
if( BST ){
if( (BST->Left == NULL) && (BST->Right == NULL)){ //找到了叶结点
printf("字符%c对应权值为%d的哈夫曼编码为:",BST->ch,BST->Weight);
for(int i=0; iLeft,depth+1);
code[depth] = 1; //往右子树方向编码为1
HuffmanCode(BST->Right,depth+1);
}
}
}
/*******************哈夫曼解码*********************/
void HuffmanDecode(char ch[],HuffmanTree BST) //ch[] 要解码的序列
{
int cnt;
int num[100];
HuffmanTree temp;
for(int i=0; iLeft != NULL ) && (temp->Right != NULL)){
if(num[cnt] == 0){
temp = temp->Left;
}else{
temp = temp->Right;
}
cnt++;
}
printf("%c",temp->ch); //输出解码后对应结点的字符
}
}
}
/*****先序遍历*****/
void PreOrderTraversal(HuffmanTree BST)
{
if( BST ){
printf("%d ",BST->Weight); //先访问根节点
PreOrderTraversal(BST->Left); //再访问左子树
PreOrderTraversal(BST->Right); //最后访问右子树
}
}
HuffmanTree NewHuffmanNode()
{
HuffmanTree BST = (HuffmanTree)malloc(sizeof(HuffmanNode));
BST->Weight = 0;
BST->Left = BST->Right = NULL;
return BST;
}
MinHeap CreateMinHeap(int MaxSize)
{ /*创建容量为MaxSize的最小堆*/
MinHeap H = (MinHeap)malloc(sizeof(struct HeapStruct));
H->data = (HuffmanTree *)malloc((MaxSize+1) * sizeof(HuffmanTree));
H->Size = 0;
H->Capacity = MaxSize;
HuffmanTree T = NewHuffmanNode();
T->ch = '\0'; //空字符
T->Weight = MinData; /*定义哨兵-为小于堆中所有可能元素权值的值,便于以后更快操作*/
H->data[0] = T;
return H;
}
bool IsFull(MinHeap H)
{
return (H->Size == H->Capacity);
}
bool IsEmpty(MinHeap H)
{
return (H->Size == 0);
}
/*插入算法-将新增结点插入到从其父结点到根结点的有序序列中*/
bool Insert(MinHeap H,HuffmanTree item)
{/*将元素item插入到最小堆H中,其中H->data[0]已被定义为哨兵*/
int i;
if( IsFull(H) ){
printf("最小堆已满\n");
return false;
}
i = ++H->Size; //i指向插入后堆中的最后一个元素的位置
for(; H->data[i/2]->Weight > item->Weight; i/=2) //无哨兵,则增加判决条件 i>1
H->data[i] = H->data[i/2]; //向下过滤结点
H->data[i] = item; //将item插入
return true;
}
HuffmanTree DeleteMin(MinHeap H)
{/*从最小堆H中取出权值为最小的元素,并删除一个结点*/
int parent,child;
HuffmanTree MinItem,temp = NULL;
if( IsEmpty(H) ){
printf("最小堆为空\n");
return NULL;
}
MinItem = H->data[1]; //取出根结点-最小的元素-记录下来
/*用最小堆中的最后一个元素从根结点开始向上过滤下层结点*/
temp = H->data[H->Size--]; //最小堆中最后一个元素,暂时将其视为放在了根结点
for(parent=1; parent*2<=H->Size; parent=child){
child = parent*2;
if((child != H->Size) && (H->data[child]->Weight > H->data[child+1]->Weight)){/*有右儿子,并且左儿子权值大于右儿子*/
child++; //child指向左右儿子中较小者
}
if(temp->Weight > H->data[child]->Weight){
H->data[parent] = H->data[child]; //向上过滤结点-temp存放位置下移到child位置
}else{
break; //找到了合适的位置
}
}
H->data[parent] = temp; //temp存放到此处
return MinItem;
}
MinHeap BuildMinHeap(MinHeap H)
{/*这里假设所有的H->Size个元素已经存在H->data[]中*/
/*本函数将H->data[]中的元素调整,使其满足堆的有序性*/
int i,parent,child;
HuffmanTree temp;
for(i=H->Size/2;i>0;i--){ //从最后一个父结点开始,直到根结点
temp = H->data[i];
for(parent=i; parent*2<=H->Size; parent=child){
/*向下过滤*/
child = parent*2;
if((child != H->Size) && (H->data[child]->Weight > H->data[child+1]->Weight)){/*有右儿子,并且左儿子权值大于右儿子*/
child++; //child指向左右儿子中较小者
}
if(temp->Weight > H->data[child]->Weight){
H->data[parent] = H->data[child]; //向上过滤结点-temp存放位置下移到child位置
}else{
break; //找到了合适的位置
}
}/*结束内部for循环对以H->data[i]为根的子树的调整*/
H->data[parent] = temp; //temp(原H->data[i])存放到此处
}
return H;
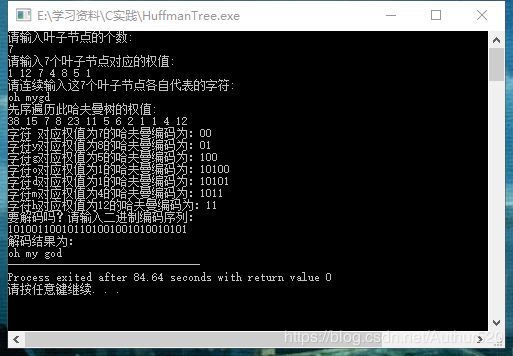
} 运行结果为: