Python声音处理入门
Python声音处理入门
注:本文加入了译者的理解,并非严谨的译作,仅供参考。
原文Basic Sound Processing with Python描述了怎样在Python中通过pylab接口对声音进行基本的处理。
准备工作
安装库
确保库numpy、matplotlib和scipy已正确安装。
导入包
from pylab import*
from scipy.io import wavfile读取wav文件
读取wav文件
下载文件440_sine.wav,文件中加入了基频(F0)为440Hz的噪声。
sampFreq, snd = wavfile.read('440_sine.wav')函数scipy.io.wavefile.read以int16或int32(32位wav)格式读入wav文件。16位.wav文件对应int16,32位.wav文件对应int32,不支持24位.wav。
查看wav文件类型
>>>snd.dtype
dtype('int16')这表示原始声压值在wav文件中一一映射到区间[-2^15, 2^15 -1]。我们把声压值归一化,即映射到区间[-1, 1):
snd = snd / (2.**15)查看wav文件的通道数和采样点数
>>> snd.shape
(5060, 2)表示文件包含2个通道,5060个采样点。结合采样率(sampFreq = 44110),可得信号持续时长为114ms:
>>> 5060.0 / sampFreq
0.11473922902494331下文我们只处理其中一个通道
s1 = snd[:, 0]python自身不支持播放声音,假如你想在python中回放声音,参考pyalsaaudio(Linux)或PyAudio。
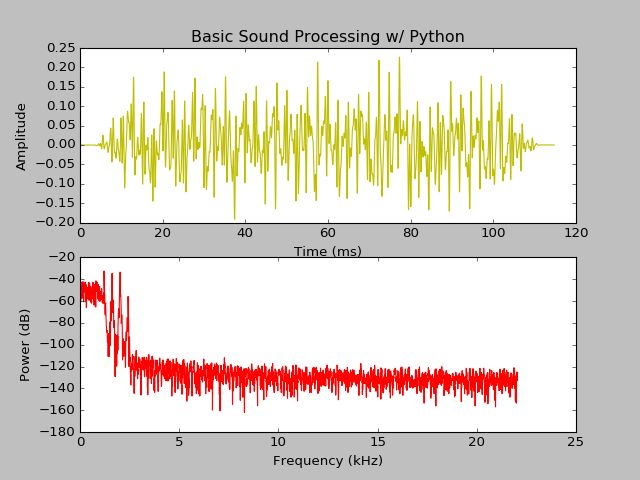
2 绘制音调图
以时间(单位ms)为x轴,声压值为y轴,绘制音调图。先创建时间点数组
timeArray = arange(0, 5060.0, 1) #[0s, 1s], 5060个点
timeArray = timeArray / sampFreq #[0s, 0.114s]
timeArray = timeArray * 1000 #[0ms, 114ms]然后绘图
plot(timeArray, s1, color='k')
ylabel('Amplitude')
xlabel('Time (ms)')- 1
- 2
- 3
3 绘制频谱图
频谱图也是一种很有用的图形表示方式。用函数fft对声音进行快速傅立叶变换(FFT),得到声音的频谱。让我们紧跟技术文档的步伐,得到声音文件的功率谱:
n = len(s1)
p = fft(s1) #执行傅立叶变换技术文档中指定了执行fft用到的抽样点数目,我们这里则不指定,默认使用信号n的采样点数。不采用2的指数会使计算比较慢,不过我们处理的信号持续时间之短,这点影响微不足道。
nUniquePts = ceil((n+1)/2.0)
p = p[0:nUniquePts]
p = abs[p]fft变换的返回结果为复合形式,比如复数,包含幅度和相位信息。我们获取傅立叶变换的绝对值,得到频率分量的幅度信息。
p = p / float(n) #除以采样点数,去除幅度对信号长度或采样频率的依赖
p = p**2 #求平方得到能量
#乘2(详见技术手册)
#奇nfft排除奈奎斯特点
if n % 2 > 0: #fft点数为奇
p[1:len(p)] = p[1:len(p)]*2
else: #fft点数为偶
p[1:len(p)-1] = p[1:len(p)-1] * 2
freqArray = arange(0, nUniquePts, 1.0) * (sampFreq / n)
plot(freqArray/1000, 10*log10(p), color='k')
xlabel('Freqency (kHz)')
ylabel('Power (dB)')绘制的频谱图如下所示。注意图中y轴是能量的对数10*log10(p),单位分贝;x轴是频率/1000,单位kHz。
为了检验计算结果是否等于信号的能量,我们计算出信号的均方根rms。广义来说,可以用rms衡量波形的幅度。如果直接对偏移量为零的正弦波求幅度的均值,它的正负部分相互抵消,结果为零。那我们先对幅度求平方,再开方(注意:开方加大了幅度极值的权重?)
rms_val = sqrt(mean(s1**2))
rms_val
0.0615000626299信号的rms等于总能量的平方根,那么把fft在所有频率上的能量值相加然后求平方根,应该等于rms。
>>> sqrt(sum(p))
0.0615000626299完整代码
转载链接:https://blog.csdn.net/shiner3089/article/details/50389330