数据结构&算法学习笔记: 归并排序

归并排序：
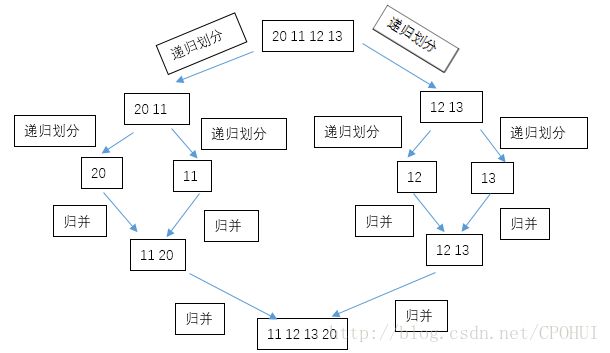
思路：每一次尽量把元素分成尽量相等的两半[x, m）， [m, y）。两半的元素分别排序(递归求解)，再把两个有序表合并成一个。(x 为排列元素起始的下标， y 为排列元素终止的下标 + 1，m 为 x + （y - x ）/ 2 )

递归出口: 当且序列元素的长度为1时，递归结束。

合并的过程: 每次把两个序列的最小元素加以比较，把最小元素加入新表。只要一个序列非空就要继续合并 ( while( p < m || q < y ) ）。因为其中一个序列为空时，因此不能直接比较A[p] 或 A[q].

• 如果第二个序列为空(q >= y)，第一个序列肯定非空，复制A[p]（第一个序列)
• 否则当且第二个序列非空，第一个序列也非空且A[p] <= A[q]时，复制A[p].

时间复杂度： O(nlogn)

void merge_sort(int* A, int x, int y, int* T)
{/*A是原数组，x 为排列元素起始的下标，y为排列元素终止的下标+1
T是辅助数组*/
    if(y - x > 1) //递归出口
    {
        int m = x + (y - x)/2;
        int p = x, q = m, i = x;
        merge_sort(A, x, m, T);//递归求解左半序列
        merge_sort(A, m, y, T);//递归求解右半序列
        while(p < m || q < y)
        {//只要一个序列非空就要继续合并
            if(q >= y || p < m && A[p] <= A[q]) 
                T[i++] = A[p++];
            else 
                T[i++] = A[q++];
        }
        for(i = x; i < y; i++)A[i] = T[i];//从辅助空间复制回数组A
    }
}

应用：求逆序对数等等。
由于归并操作是从小到大进行的，当右边的A[q]复制到T中, 左边没来得及复制到临时数组T中的就是左边所有比A[q]大的数。值得注意的是对于划分的数列，左边划分的数列的排列顺序相对于右边的数列所产生的逆序对无关。如(20,12) 和（13，19）与 （12，20）和（13，19）左边相对于右边的逆序对都为2.（（20，13），（20，19）），所以归并过程中的逆序对和分块差不多。在代码上唯一修改else T[i++] = A[q++];改成else {T[i++] = A[q++]; cnt += m - p;}//左边所剩的元素在[p,m)中元素个数为m - p
题目：HDU 1394 (传送门)Minimum Inversion Number
Time Limit: 2000/1000 MS (Java/Others)
Memory Limit: 65536/32768 K (Java/Others)

Problem Description
The inversion number of a given number sequence a1, a2, …, an is the number of pairs (ai, aj) that satisfy i < j and ai > aj.

For a given sequence of numbers a1, a2, …, an, if we move the first m >= 0 numbers to the end of the seqence, we will obtain another sequence. There are totally n such sequences as the following:

a1, a2, …, an-1, an (where m = 0 - the initial seqence)
a2, a3, …, an, a1 (where m = 1)
a3, a4, …, an, a1, a2 (where m = 2)
…
an, a1, a2, …, an-1 (where m = n-1)

You are asked to write a program to find the minimum inversion number out of the above sequences.

Input
The input consists of a number of test cases. Each case consists of two lines: the first line contains a positive integer n (n <= 5000); the next line contains a permutation of the n integers from 0 to n-1.

Output
For each case, output the minimum inversion number on a single line.

Sample Input
10
1 3 6 9 0 8 5 7 4 2

Sample Output
16

思路：对于这道题目，先用归并排序对原序列进行求逆序对。然后在每次产生新数列的过程中，减去因为这个新数列而减少的逆序对数，加上因为这个新数列而增加的逆序对数( 换句话说就是减去比序列首元素小的数的数目, 加上比比序列首元素大的数的数目。如（2,3,0,1）的逆序对数为4.那么(3,0,1,2)逆序对为4 - 2 + (4 - 2 - 1) = 3.）

#include
#include
#define maxn 5005
using namespace std;

int cnt;
void merge_sort(int* A, int x, int y, int* T)
{
    if(y - x > 1)
    {
        int m = x + (y - x)/2;
        int p = x, q = m, i = x;
        merge_sort(A, x, m, T);
        merge_sort(A, m, y, T);
        while(p < m || q < y)
        {
            if(q >= y || p < m && A[p] <= A[q])
                T[i++] = A[p++];
            else{
                T[i++] = A[q++];
                cnt += m - p;
            }
        }
        for(int i = x; i < y; i++)
            A[i] = T[i];
    }
}
int T[maxn];
int A[maxn];
int B[maxn];
int main()
{
    int n;
    //freopen("input.txt","r",stdin);
    while(~scanf("%d",&n))
    {
        for(int i = 0; i < n; i++)
        {
            scanf("%d",&A[i]);
            B[i] = A[i];
        }
        cnt = 0;
        merge_sort(B,0,n,T);
        int ans = cnt;
        for(int i = 0; i < n - 1; i++)
        {
            cnt -= A[i];
            cnt += (n - A[i] - 1);
            if(ans > cnt)ans  = cnt;
        }
        printf("%d\n",ans);
    }
    return 0;
}