数据结构和算法分析之排序算法--插入排序篇（直接插入排序和希尔排序）

排序算法的概述

---

排序有内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。本系列介绍的都是内部排序。

其中： 当n较大，则应采用时间复杂度为O(nlog2n)的排序方法：快速排序、堆排序或归并排序序。
快速排序：是目前基于比较的内部排序中被认为是最好的方法，当待排序的关键字是随机分布时，快速排序的平均时间最短；

1. 插入排序–直接插入排序

---

基本思想:
将一个记录插入到已排序好的有序表中，从而得到一个新的记录数曾1的有序表。即：先将序列的第1个记录看成一个有序的子序列，然后从第2个记录逐个进行插入，直至整个序列有序为止。
关键点：设置比较参数，作为临时存储和判断数字边界之用。
举例如下：

若比较发现和插入元素相等的，那么插入元素把想插入的元素放在相等元素的后面。插入排序是很稳定的。

**

直接插入排序的算法思路：

**
1、每次插入，插入数被选择成监视岗，此处记为tmp。将tmp值和前一个数进行比较，大于则直接放在原位；（默认排序方式从小到大），若小于，进行后续操作。

如图：i=2中，38小于49，把38赋予tmp,然后把49放到后面一个位置。
2、tmp值小于前一个值，这里记为a[i-1]，需要向前依次比较，查找插入位置。首先将a[i-1]向后移动一位，给前面插入提供一个插入位置。

如图：i=2中，把49向后移动一位，就是为插入数提供一个空位置。
3、比较tmp和a[i-2],若tmp大于a[i-2],直接插入a[i-1]的位置即可；若小于，则需要把tmp值再和a[i-2]前面一个值比较（这里需要注意的是，若a[i-2]不存在，则计算机显示的数值是一个极小值，也会包含在判断内）

如图：i=4，此时各参数是：tmp=76, i=5, j=4。首先把97放到a[i]的位置，然后进入循环。tmp每次和a[j]比较，小于就把a[j]向后移动一位；大于或等于，tmp就放在比较数a[j]的后面位置a[j+1]上。
再如i=5，其中包含了一种特殊情况，tmp值和a[0]比较后，将a[0]向后移动一位，j–；此时的a[-1]不存在，在计算机内表示为极小值。因此也无法进入循环，因此Tmp就放在当前位置a[j]处。这里的j–就是插入位置向前移动的标志。

效率：时间复杂度：O（n^2）

分析：由于嵌套循环的每一个都花费N次迭代，因此插入排序为O（N^2）。（外层循环N次，内层也是N次）；精确计算，对于i的每一个值，最多执行i+1次。对所有的i求和，得到总数为：
)
因此时间复杂度是不考虑系数的。

代码如下：

#include 
using namespace  std;

void print(int a[],  int n, int i)
{
    cout<":"<<" ";
    for(int j=0;jcout<" ";
    }
    cout<void InsertSort(int a[],int n)
{
    int tmp;
    for(int i=1;iif(a[i]1])
        {
            a[i]=a[i-1];//先把第i-1个元素后移一位
            int j=i-1;
            //找第i元素的插入位置
            while(tmp1]=a[j];
                j--;

            }
            a[j+1]=tmp;
        }
        print(a,n,i);
    }

}

int main()
{
    int a[8]={49,38,65,97,76,13,27,49};
    InsertSort(a,8);
    system("pause");
    return 0;
}

结果展示：

总结：直接插入排序可以简述为以下步骤：
1、比较插入值和前面一个值的大小；
2、小于的情况：移一位空位置，然后循环与前位比较，注意插入位置用j–确定；
3、小于继续向前比较，大于放在j的位置。

注意：直接插入排序的时间复杂度为O（n^2）;

---

2. 插入排序–希尔排序

希尔排序对于直接插入排序来说，有较大的改进。希尔排序又称缩小增量排序。

基本思想：将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，将整个序列中的记录“基本序列”时，再对全体记录进行依次直接插入排序。

操作方法：

1. 选择一个增量序列t1, t2, … , tk, 其中ti>tj , tk=1;
2. 按增量序列个数k，对序列进行k趟排序；
3. 每趟排序，根据对应的增量ti ，将待排序分割成若干长度为m的子序列，分别对各子表进行直接插入排序。当且仅当增量因子为1时，整个序列当成一个表爱处理，表长度就是整个序列长度。

希尔排序实例：

算法实现：

我们简单处理增量序列：增量序列d={n/2,n/4,n/8……1}n为要排序数的个数
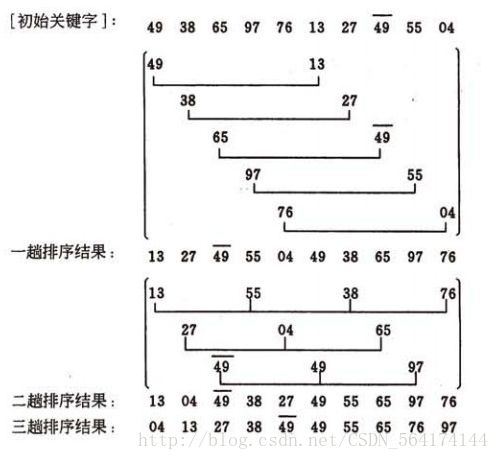
即：先将要排序的一组记录按某个增量d(n/2,n为要排序数的个数)分为若干组子序列，每组中记录的下标相差d,对每组中全部元素进行直接插入排序，然后再用一个较小的增量（d/2）对它进行分组，在每组中再进行直接插入排序，如此循环，不断缩小增量直至为1，最后对全序列进行直接插入排序。

效率：时间复杂度–希尔排序

希尔排序的时间复杂度很难分析，关键的是比较次数与记录移动次数依赖于增量因子序列dk的选取，特殊情况下可以准确估算出关键码的比较次数和记录移动的次数。目前几种取增量因子序列几种常见取法，取2的倍数，取质数。需要注意：最后一个增量因子必须是1。希尔排序方法是一个不稳定的排序方法。

希尔排序的最坏情形分析：
N取2的幂，增量因子取2的倍数。给出例子为偶数位置上有N/2个同是最大的数，奇数位置上有N/2个同为最小的数，且都是依次增大的，如：a={1,9,2,10,3,11,4,12,5,13,6,13,7,14,7,15,8,16}。最后一次排序的逆序数正好是1+2+…+N=(1+N)*N/2=O(N^2)；
因此得到结论是：希尔排序的最坏时间复杂度是O（N^2）。

完整代码如下：

#include
using namespace std;

void print(int a[], int n ,int i){  
    int dk;
    printf("dk=%d ",i);
    for(int j= 0; jcout<" ";  
    }  
    cout<void ShellInsertSort (int a[],int n,int dk)
{
    for(int i=dk;iif(a[i]int tmp=a[i];
            a[i]=a[i-dk];//移一位
            int j=i-dk;
            while(tmp//预定义增量因子是ak/2;
void ShellSort(int a[],int n)
{
    int dk=(n/2);
    while(dk>=1)
    {
        ShellInsertSort(a,n,dk);
        dk=dk/2;
    }
}

int main()
{
    int a[] = {49,38,65,97,76,13,27,49,55,04};  
    ShellSort(a,10);
    //print(a,10,10);
    system("pause");
    return 0;
}

---

测试结果如下：

资料引用：
http://blog.csdn.net/hguisu/article/details/7776068/
特别鸣谢~