关系数据库设计理论
一、关系数据库模型
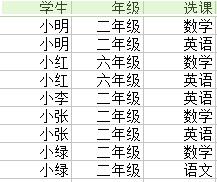
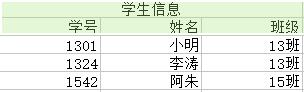
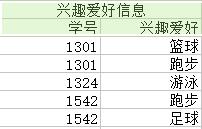
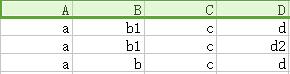
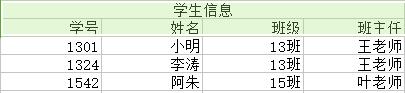
关系模型是一种基于表的数据模型,以下为关系学生信息,该表有很多不足之处,本文研究内容就是如何改进它:
下面是一些重要术语:
1.属性(attribute):列的名字,上图有学号、姓名、班级、兴趣爱好、班主任、课程、授课主任、分数。
2.依赖(relation):列属性间存在的某种联系。
3.元组(tuple):每一个行,如第二行 (1301,小明,13班,篮球,王老师,英语,赵英,70) 就是一个元组
4.表(table):由多个属性,以及众多元组所表示的各个实例组成。
5.模式(schema):这里我们指逻辑结构,如 学生信息(学号,姓名,班级,兴趣爱好,班主任,课程,授课主任,分数) 的笼统表述。
6.域(domain):数据类型,如string、integer等,上图中每一个属性都有它的数据类型(即域)。
7.键(key):由关系的一个或多个属性组成,任意两个键相同的元组,所有属性都相同。需要保证表示键的属性最少。一个关系可以存在好几种键,工程中一般从这些候选键中选出一个作为主键(primary key)。
8.候选键(prime attribute):由关系的一个或多个属性组成,候选键都具备键的特征,都有资格成为主键。
9.超键(super key):包含键的属性集合,无需保证属性集的最小化。每个键也是超键。可以认为是键的超集。
10.外键(foreign key):如果某一个关系A中的一个(组)属性是另一个关系B的键,则该(组)属性在A中称为外键。
11.主属性(prime attribute):所有候选键所包含的属性都是主属性。
12.投影(projection):选取特定的列,如将关系学生信息投影为学号、姓名即得到上表中仅包含学号、姓名的列
13.选择(selection):按照一定条件选取特定元组,如选择上表中分数>80的元组。
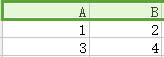
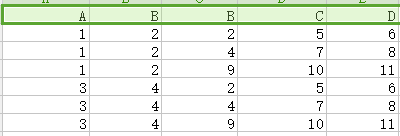
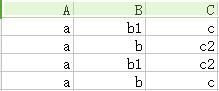
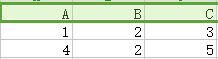
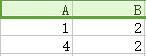
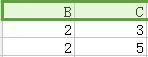
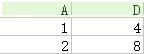
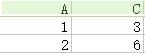
14.笛卡儿积(交叉连接Cross join):如下图,第一个关系每一行分别与第二个关系的每一行组合。
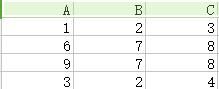
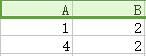
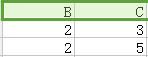
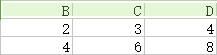
15.自然连接(natural join):如下图,第一个关系中每一行与第二个关系的每一行进行匹配,如果得到有交叉部分则合并,若无交叉部分则舍弃。
16.θ连接(theta join):即加上约束条件的笛卡儿积,先得到笛卡儿积,然后根据约束条件删除不满足的元组。
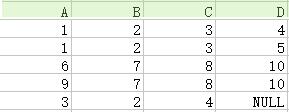
17.外连接(outer join):执行自然连接后,将舍弃的部分也加入,并且匹配失败处的属性用NULL代替。
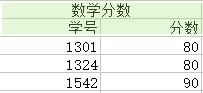
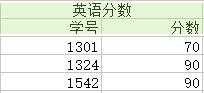
18.除法运算(division):关系R除以关系S的结果为T,则T包含所有在R但不在S中的属性,且T的元组与S的元组的所有组合在R中。下例足以说明,为了得到所有选了数学、英语并且是二年级的学生,我们用到除法运算。
二、函数依赖
1.函数依赖(functional dependency,FD)定义:
在一个关系中,任意元组,若属性A1,A2....An一样,则属性B1,B2...Bm必一样,那么称A1,A2...An函数决定B1,B2...Bm。
记号为 A1,A2...An → B1,B2...Bm (Ai与Bi有函数依赖)
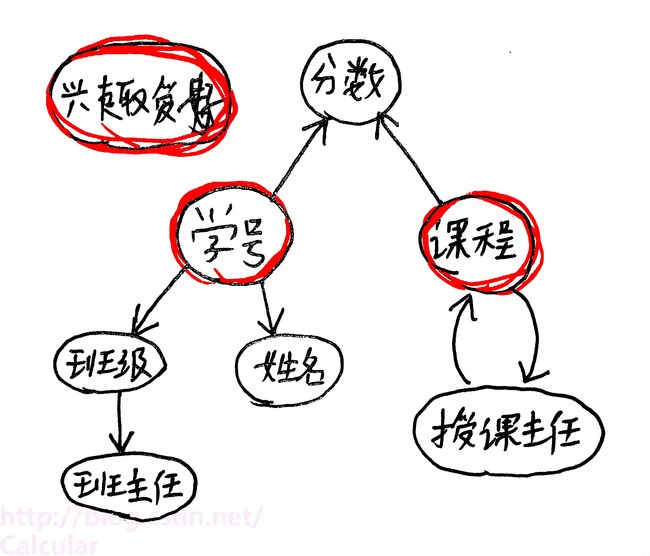
上图中,若 学号 相同,则 姓名、班级、班主任 也必然相同,用这个道理我们可以粗略得出如下函数依赖:
学号 → 姓名,班级 (每一个学号对应一个姓名和班级,但由于可能重名,一个姓名不一定只对应一个学号)
班级 → 班主任 (一个班级对应一个班主任,但我们不排除一个老师任两个班的班主任,即一个班主任可能对应多个班级)
学号,课程 → 分数 (一个学号一个课程对应一个唯一的分数)
课程 → 授课主任 (一个课程对应一个授课主任)
授课主任 → 课程 (一个授课主任只能负责一门课程)
2.Armstrong aximos规则:
传递律(Transitivity):R(A,B,C) 其中R为关系,ABC均为属性。若A → B 和 B → C 则 A → C 。
增长律(Augmentation):如果 A → B,则AC → BC,延长函数依赖不变。
自反律(Reflexivity):如果 属性集合B 属于 属性集合A,那么 A → B,这个又称为平凡函数依赖(见3)。
3.平凡函数依赖:
这里的平凡(trivial)又有无价值、琐碎的意思,理解上就是说了等于白说。
如 学号,姓名 → 学号 就是一个平凡函数依赖,因为右边的属于左边的,属于无价值信息。
4.分解/结合规则:
A1,A2...An → B1,B2...Bm 等效于 A1,A2...An → B1 ; A1,A2...An → B2 ; ..... A1,A2...An → Bm 。右边是可以拆开、合并的。
5.属性的闭包(closure):
用一个例子来说明
已知关系的所有属性集合{A,B,C,D,E,F}。
已知函数依赖 AB → C , BC → AD , D → E , CF → B 。
求{A,B}的闭包 (我们用 {A,B}+ 来表示)。
解:
<1>——分解函数依赖,使右边只有一个属性。 AB → C ; BC → A ; BC → D ; D → E ; CF → B 。
<2>——用{A,B}集合与这些函数依赖推导出新的属性加入集合,直到这个集合不再增长,此时该集合就是{A,B}+(闭包)。
容易发现 {A,B}+ = {A,B,C,D,E}。
实际上,求集合C的闭包C+,就是由全部函数依赖以及C,推导出所有能够推导的属性集合 与 C的 并集。
闭包算法能找到所有正确的函数依赖————反过来,已知 {A,B},{A,B}+,我们就能列出所有能用{A,B}推导出的函数依赖。
6.判定、计算键:
(1)运用闭包算法判断是否够是键:
要验证{A1,A2...An}是否是关系的键,可以先检查“{A1,A2...An}+是否包含了关系的全部属性”,再检查“不存在从{A1,A2...An}中移出一个属性后的集合C,使得C+包含关系的全部属性”。
(2)图解计算键:
用一个例子来说明
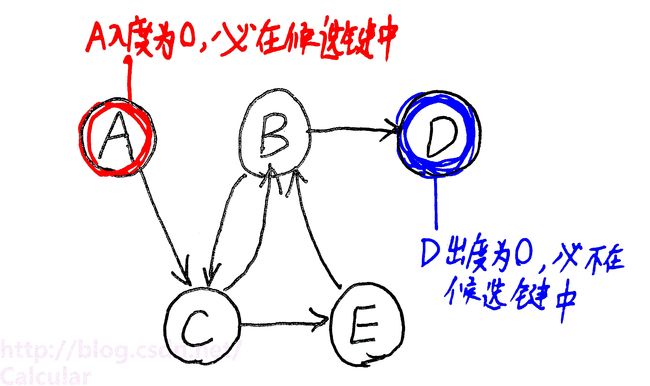
已知 {A,B,C,D,E} : AB → C , B → D , C → E , CE → B
<1>——根据依赖关系画出关系图,入度为0的必在键中,出度为0的必不在键中,如下图
现在可知,键中必有A,必无D。
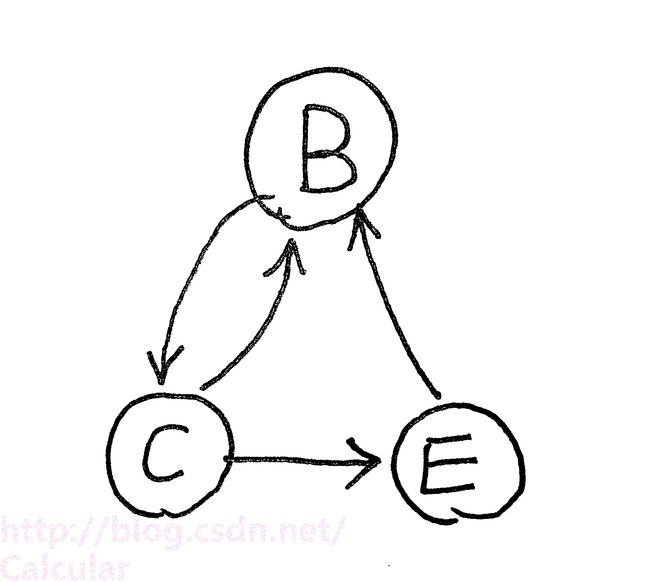
<2>——将入度或出度为0结点删去,化简依赖图,如下图
<3>——选择所有不能相互推导的属性集合,逐一检查能否遍历上面的图(注意,依赖图中只有入度全满足才算可推导)
上图中不能相互推导的集合有:{B}能遍历全图,{C}能遍历全图,{E}不能遍历全图(单个E不能满足B的全部入度)
(这里,考虑一下{B,E},因为从B出发能遍历到E,连通,所以不检查)
<4>——把上一步算出的集合分别与第1步中入度为0的点组合,最终得到候选键。
本例中候选键为 {A,B}、{A,C} 。
7.函数依赖的基本集:
(1)相关定义:
基本集:对于一个给定的函数依赖集合S,存在多个等效的函数依赖集合,任何与S等效的函数依赖集合都被称为S的基本集。
最小化基本集(minimal basis):需要满足以下条件
(1)所有函数依赖的右边均为单一属性。(右边最简)
(2)删除其中任何之一就不再是基本集。(数量最少)
(3)对于任意一个函数依赖,若其左边删除一个或多个属性,则不再是基本集。(左边最简)
(2)计算最小化基本集:
用一个例子来说明
已知 {A,B,C,D,E} : AB → CD , B → D , C → E , CE → B , AC → B
<1>——首先把右边都变成单一属性
AB → C , AB → D , B → D , C → E , CE → B , AC → B
<2>——对于每一个X → A,拟删除,再看{X}+是否能得到A
检查AB → C,拟删除,计算{A,B}+ ={A,B,D}得不到C,保留。
检查AB → D,拟删除,计算{A,B}+ ={A,B,D,E}能得到D,删除
删除之后得到(AB → C , B → D , C → E , CE → B , AC → B)
检查B → D,拟删除,计算{B}+ ={B}得不到D,保留。
检查C → E,拟删除,计算{C}+ ={C}得不到E,保留。
检查CE → B,拟删除,计算{C,E}+ ={C,E}得不到B,保留。
检查AC → B,拟删除,计算{A,C}+ ={A,B,C,D,E}能得到B,删除。
删除之后得到(AB → C , B → D , C → E , CE → B)
<3>——对于每一个X(X1,X2...) → A,依次检查Xi,检查{X-Xi}+是否能得到A,若能则用X-Xi取代X
检查AB → C,{A}+={A}得不到C,{B}+={B,D}得不到C。
检查CE → B,{C}+={C,E,B,D}能得到B,改为C → B。
因此最后得到最小化基本集为:AB → C , B → D , C → E , C → B 。
8.投影函数依赖:
用一个例子来说明
已知关系R (A,B,C,D) 。
已知函数依赖 A → B ; B → C ; C → D 。
求函数依赖在属性 (A,C,D) 上的投影(即删除原来属性B)。
解:
(1)求{A,C,D}所有子集的闭包,列出所涉及函数依赖(该函数依赖中只能出现A,C,D):
{A}+ = {A,B,C,D} : A → C、A → D (推导出的,还有一个A → B因为涉及B直接丢弃)
{C}+ = {C,D} : C → D
{D}+ = {D} : 无
{A,C}+ = {A,B,C,D} : 与第一个涉及的函数依赖一样
{A,D}+ ={A,B,C,D} : 与第一个涉及的函数依赖一样
{C,D}+ = {C,D} : 无
{A,C,D}+ = {A,B,C,D} : 与第一个涉及的函数依赖一样
(2)最小化基本集:
A → C、A → D、C → D事实上已经是最小化基本集了,本例这个就是答案。
三、多值依赖
1.多值依赖(multivalued dependency,MVD)定义:
设R(U)是属性集U上的一个关系模式,X,Y,Z是U的子集,并且Z=U-X-Y。关系模式R(U)中多值依赖 X → → Y 成立,即对于每一个(X,Z)有多个Y与之对应,并且Y的取值仅与X有关与Z无关。
多值依赖是两个属性或属性集合之间相互独立的宣言,我们可以认为当A → → B时,相同A下,(B)与(非A非B)相互独立。
这里有一个更浅显的意思,即若A → → B,则A与B是一对相关项,A与(非A非B)也是一对相关项,B与(非A非B)是一对毫不相干的项(相关指存在某种联系),这样也就解释了为何对于每一个函数依赖同时也是多值依赖(唯一决定肯定是相关的),而每一个多值依赖不一定是函数依赖(相关不一定是唯一决定)。
2.多值依赖的举例:
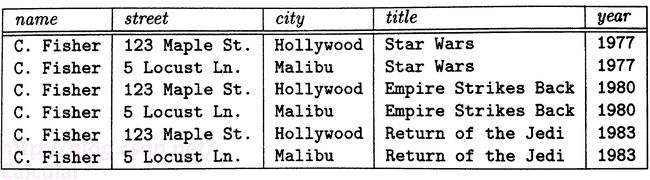
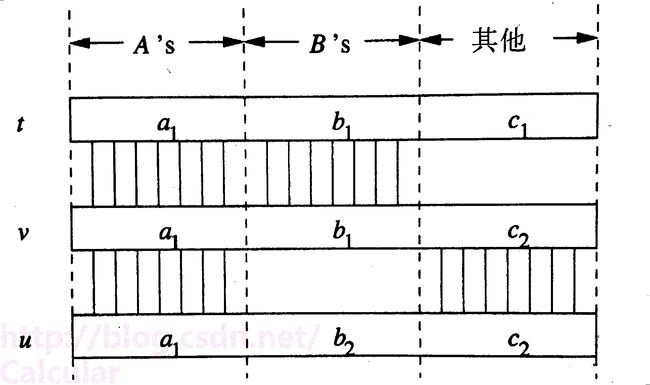
上图中,name表示一个明星的名字,street和city表示明星的住址(一个明星可以有好多住址),title和year表示该明星参演的某部电影的名字和上映时间。
对一个每一个确定的name与title,year,存在多个street,city,并且仅与name相关,或者说对于同一个明星他的住址与参演电影信息是独立的,因此可以推断:
name → → street,city
name → → title,year (实质上由于多值依赖的互补性,这两者是等效的)
这种属性之间的独立性会产生冗余,上图中,每个地址出现了三次,每个电影也出现了两次,我们需要一些方法消除多值依赖引起的冗余(接下来会在第四范式中提到)。
3.多值依赖的判别:
如果能在属性A相同的情况下找到三个元组t、v、u,使
<1>——对于B属性,v与t相同。(注:v与u可以不同可以相同,其实若B不属于A肯定不同)
<2>——对于除了AB之外的其他属性,v与u相同。(注:v与t可以不同可以相同,其实若B不属于A肯定不同)
则 A → → B (或者A → → 非A非B,这是互补性的体现)。
4.多值依赖的规则(MVD为多值依赖的缩写):
(1)平凡MVD:和函数依赖一样,例如 name,street → → street 只要右边属于左边就一样成立。
(2)传递规则:若X → → Y、Y → → Z 则 X → → Z-Y。(结果中除去Z中属于Y的属性)
(3)右边不能分解:若name → → street,city 则不能分解成 name → → street 。
(4)FD推导MVD:若A1...An → B1...Bm(函数依赖),则必然A1...An → → B1...Bm(多值依赖)。
(5)互补规则(complementation rule):若A → → B ,则 A → → 非A非B 。
(6)附加平凡MVD:若某关系的所有属性为{A1,A2...An,B1,B2...Bm},则A1,A2...An → → B1,B2...Bm。
5.MVD发现算法——chase扩展到MVD:
用一个例子来说明。
已知 {A,B,C,D} : A → B , B → → C
需要证明:A → → C成立。
解:
<1>——首先根据需证明的结果A → → C建立一张初始化表,如下图这张初始化表只有两行,两行都填入有相同的属性A,且不带下标,然后
第一行:属性C中填入不带下标的,其余空带下标。
第二行:属性(非A非C)中填不带下标的,C中填带下标的
<2>——根据函数依赖A → B调整表,A相同的B全写相同(优先选无下标的),如下图<3>——根据多值依赖B → → C,找到B相同的两行(其实只有两行了),复制这两行,并把这个副本中的C列对调,将其放到表的下面拼成一个四行的表,如下图
只要出现全部无下标的一行(图中第四行),则证明成立。
6.多值依赖的投影——应用MVD发现算法:
用一个例子来说明
已知 R {A,B,C,D,E} : A → → CD
问这个多值依赖是否蕴含着某些在S(A,B,C)上成立的依赖。
解:
首先根据上述多值依赖,很容易想到A → → C在S上成立(S没有D属性,因此去掉了),运用MVD发现算法证明之。
<1>——根据A → → C与S的属性A,B,C构建初始化表,如下图(参见MVD发现算法)
<2>——根据多值依赖A → → CD,先复制两行,将这个副本的CD两列对调,再放到表下面,拼成一个四行的表。注意这个表没有D列,就当它是空气了,只要对调C列就行。如下图
<3>——我们找到了没有下标的行(第四行),证明成立。
四、关系数据库模式设计要领
1.关系数据库可能产生的异常(anmoaly):
(1)冗余(redundancy):上图关系中 学号、姓名、班级、兴趣爱好、班主任、课程 、授课主任列中包含多个重复值。
(2)更新异常(update anomaly):若更换了13班的班主任,仅仅更新第一行的信息是不够的,为此还要大费周折更新第二、三、四、五行的班主任信息。
(3)删除异常(deletion anomaly):若小明英语缺考,我们需要删除二、三行的全部信息,但是同时也不必要地删除了小明的跑步兴趣爱好。
实际上,发送异常的主要原因是,冗余和关联。
2.分解关系(decompose):
为了消除上图中的各种异常,我们将关系分解成六个,如下图(注:分解都是按列分解的)
(1)对于冗余:极大地减少了数据的重复次数,实际上已经消除到最佳。
(2)对于更新异常:若更换了13班的班主任,仅仅需要更新班主任信息的第一行。
(3)对于删除异常:若小明英语缺考,我们仅需要删除英语分数的第一行。
3.分解的优略:
(1)消除异常(Elimination of Anomalie):
(2)信息的可恢复(Recoverability of Information),即 无损连接:能否从分解后的各元组中恢复分解前的各元组。
(3)依赖的保持(Preservation of Dependencies):能否从分解后的函数依赖投影中恢复原先的函数依赖。
4.从分解中恢复信息:
(1)有损连接的无法恢复:
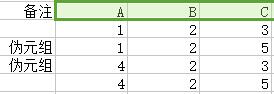
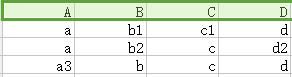
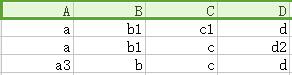
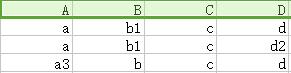
用一个例子来说明,下图为某一关系的分解,分解前关系的函数依赖为 A → C 。
如果需要恢复,则执行自然连接,如下图:
我们可以看到,出现两个伪元组,这些伪元组无法判别真伪,因此无法恢复。
(2)无损连接(lossless join):
如果能从 分解后所有关系的元组 中通过自然连接 恢复 之前的各元组,则称该分解含有无损连接。
(3)判别是否含有无损连接,chase检验:
用一个例子来说明
已知分解前的关系 {A,B,C,D} 被分解为三个关系,分别为 {A,D}、{A,C}、{B,C,D},
若分解前(不投影)的 函数依赖 为 A → B 、 B → C 、 CD → A,
判断是否含有无损连接。
解:
<1>——首先,根据分解后包含哪些属性({A,D}、{A,C}、{B,C,D})初始化一张表,如下
上表中,每一行对应一个分解的关系。
第一行对应{A,D},将A与D属性值设置成不带下标的a、d,其他属性都带下标1。
第二行对应{A,C},将A与C属性值设置为不带下标的a、c,其他属性都带下标2。
第三行对应{B,C,D},将B与C与D属性值设置为不带下标的b、c、d,其他属性都带下标3。
<2>——表初始化完成,接下来逐一根据 函数依赖 更改表中值。
根据依赖A → B,将A相同的所有B改相同(优先选择无下标的),如下图
根据依赖B → C,将B相同的所有C改相同(优先选择无下标的),如下图
根据依赖CD → A,将C、D相同的所有A改相同(优先选择无下标的),如下图
<3>——判断,若存在全部为不带下标的行(如上图中第三行),则为无损连接(上述即含有无损连接)。
下面给一个上述无损连接恢复的例子:
结果就是原表(可以动手推一下)。
五、关系数据库常用分解模式
1.第一范式(1NF):
可以认为任何表都属于第一范式,因为每个表的最小单位为表中的各个属性。
一般在分解之前,我们先求出所有候选键,从中挑选出一个作为主键,然后最小化函数依赖基本集。
上述表肯定是符合第一范式的,我们先得到如下信息: (我们先按照前面说的方法确定主键和函数依赖的最小基本集)
候选键为 学号、课程、兴趣爱好 和 学号、授课主任、兴趣爱好,我们一般选一个作为主键。
学生信息{学号,姓名,班级,兴趣爱好,班主任,课程,授课主任,分数}
学号 → 姓名,班级 ; 班级 → 班主任 ; 学号,课程 → 分数 ; 课程 → 授课主任 ; 授课主任 → 课程
2.第二范式(2NF):
(1)定义:
A relation is in 2NF if it is in 1NF and no non-prime attribute is dependent on
any proper subset of any candidate key of the relation.
在满足第一范式前提下,在所有函数依赖表达式中,不存在任何候选键的真子集决定非主属性,
即消除非主属性对于键的部分依赖。
(2)分解规则:
我们可以从上图中得出
候选键:{学号,兴趣爱好,课程}、{学号,兴趣爱好,授课主任}
主属性:学号、兴趣爱好、课程、授课主任
非主属性:班级、姓名、班主任、分数
由于存在 学号 → 姓名 ; 学号 → 班级 ; 学号 → 班级 → 班主任 ; 学号,课程 → 分数 等非主属性由键的一部分决定,因此不满足第二范式,需要分解。
分解为如下三张表:
<1>——学生信息 {学号,姓名,班级,班主任} :
候选键:{学号}
主属性:学号
非主属性:姓名、班级、班主任
函数依赖在这上面的投影为:学号 → 姓名 ; 学号 → 班级 ; 班级 → 班主任
由于 学号 → 姓名 ; 学号 → 班级 ; 学号 → 班级 → 班主任 非主属性由键(而非键的一部分)决定,因此满足第二范式。
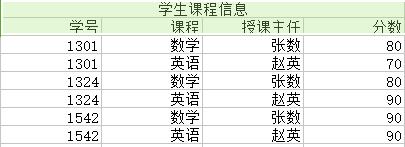
<2>——学生课程信息 {学号,课程,授课主任,分数} :
候选键:{学号,课程}、{学号,授课主任}
主属性:学号、课程、授课主任
非主属性:分数
函数依赖在这上面的投影为:学号,课程 → 分数 ; 学号 → 班级 ; 学号 → 班级 → 班主任
由于非主属性由键(而非键的一部分)决定,因此满足第二范式。
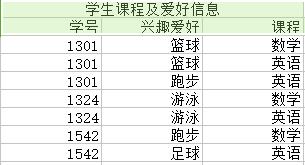
<3>——学生课程及爱好信息 {学号,课程,兴趣爱好} :
候选键:{学号,兴趣爱好,课程}
主属性:学号、兴趣爱好、课程
非主属性:无
函数依赖在这上面的投影为:无
由于非主属性(这里没有非主属性,必然满足)由键(而非键的一部分)决定,因此满足第二范式。
最终得到的分解结果如下:
(3)分解效果:
对于冗余:极大地减少了数据的重复次数,不过仍然存在冗余
对于更新异常:若更换了13班的班主任,仅需要访问两个元组,比之前方便了点。
对于删除异常:若小明英语缺考,我们需删除学生课程信息的第二行,但同时也删除了赵英的信息,有风险。
3.第三范式(3NF):
(1)定义:
The relation R (table) is in second normal form (2NF). Every non-prime attribute of R is non-transitively dependent on every key of R.
在满足第二范式前提下,在所有函数依赖表达式中,所有非主属性不传递依赖于候选键,这里A → B , B → C则称C传递依赖于A,
即消除非主属性对于键的部分依赖、传递依赖。
(2)分解规则:
对于2NF分解结果中的第一个表学生信息 {学号,姓名,班级,班主任}
候选键:{学号}
主属性:学号
非主属性:姓名、班级、班主任
函数依赖:学号 → 姓名 ; 学号 → 班级 ; 班级 → 班主任
由于 学号 → 班级 → 班主任 存在非主属性传递依赖于候选键,因此不满足第三范式,需要分解。
该表分解为如下两张表:
<1>——学生信息 {学号,姓名,班级} :
候选键:{学号}
主属性:学号
非主属性:姓名、班级
函数依赖在这上面的投影为:学号 → 姓名 ; 学号 → 班级
由于 不存在非主属性传递依赖于候选键,因此满足第三范式。
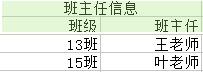
<2>——班主任信息 {班级,班主任} :
候选键:{班级}
主属性:班级
非主属性:班主任
函数依赖在这上面的投影为:班级 → 班主任
由于 不存在非主属性传递依赖于候选键,因此满足第三范式。
最终得到的分解结果如下:
(3)分解效果:
对于冗余:极大地减少了数据的重复次数
对于更新异常:若更换了13班的班主任,仅需要访问一个元组,该异常消除了,但如果更换授课主任任然有异常。
对于删除异常:若删除某个班主任,仅访问一个元组,不存在风险。
4.Boyce-Codd范式(BCNF,3.5NF):
(1)定义:
X → Y is a trivial functional dependency (Y 属于 X),X is a superkey for schema R
在所有(平凡)函数依赖表达式中,箭头左边都是超键(可以推导出它必满足第三范式),
即消除任何属性对于键的部分依赖、传递依赖。
(2)分解规则:
对于3NF分解结果中的第三个表学生课程信息 {学号,课程,授课主任,分数}:
候选键:{学号,课程}、{学号、授课主任}
所有属性:学号、课程、授课主任、分数
函数依赖:学号,课程 → 分数 ; 课程 → 授课主任 ; 授课主任 → 课程
由于 课程 → 授课主任 、 授课主任 → 课程 存在箭头左边不是超键,因此不满足BCNF范式,需要分解。
该表分解为如下两张表:
<1>——课程分数信息 {学号,课程,分数} :
候选键:{学号,课程}
函数依赖在这上面的投影为:学号,课程 → 分数
由于 箭头左边是键,因此满足BCNF范式。
<2>——授课主任信息 {课程,授课主任} :
候选键:{课程}、{授课主任}
函数依赖在这上面的投影为:课程 → 授课主任
由于 箭头左边是键,因此满足BCNF范式。
最终得到的分解结果如下:
(3)分解效果:
对于冗余:极大地减少了数据的重复次数
对于更新异常:若更数学授课主任,仅需要访问一个元组,该异常消除了。
对于删除异常:若小明英语缺考,仅访问课程分数表中一个元组,删除之,不存在风险。
5.第四范式(4NF):
(1)定义:
for every one of its non-trivial multivalued dependencies X -> Y, X is a superkey.
在所有(平凡)多值依赖表达式中,箭头左边都是超键(由于每个函数依赖也是多值依赖,可以推导出它必满足Boyce-Codd范式),
即消除任何属性对于键的部分多值依赖、传递多值依赖。(注:函数依赖也属于多值依赖)
(2)分解规则:
对于BCNF分解结果中的第五个表学生课程及爱好信息 {学号,兴趣爱好,课程}:
存在三个行:第一行,第二行,第三行,使
在学号相同的情况下,第二行的兴趣爱好根第一行的相同,第二行的课程又根第三行相同。
因此存在多值依赖 学号 → → 兴趣爱好 (由于互补性,学号 → → 课程 也成立)
候选键:{学号,兴趣爱好,课程}
由于该多值依赖左边不是超键,因此不满足第四范式,需要分解。
该表分解为如下两张表:
<1>——兴趣爱好信息 {学号,兴趣爱好} :
候选键:{学号}
多值依赖在这上面的投影为:学号 → → 兴趣爱好,这个可以直接退化为 学号 → 兴趣爱好
由于 箭头左边是键,因此满足第四范式
<2>——学号课程信息 {学号,课程} :注意!!此表是之前课程分数信息表的子集,可以直接删去。
最终得到的分解结果如下:
(3)分解效果:
对于冗余:消除了所有冗余
对于更新异常:若更新小明的兴趣爱好,仅需要访问一个元组,该异常消除了。
对于删除异常:若删除小明跑步的兴趣爱好,仅删除兴趣爱好信息中的一个元组,删除之,不存在风险。
例题1:
Which items can determine all attributes in a relation:
A.super key B.foreign key C.candidate key D.primary key
解答:
我们知道,候选键(包含主键) → 任何属性 , 超键 → 任何属性 。由于主键是候选键的子集,候选键又是超键的子集,我们选择A、C、D。
例题2:
In a relational database, given R
A.lossless-join, dependency preserving B.lossless-join, not dependency preserving
C.lossy-join, dependency preserving B.lossy-join, not dependency preserving
解答:
如果将{A,B,C} : A → B,B → C,C → A 划分为{A,B}、{B,C} ,是否有无损连接和依赖保持。
检验无损连接:
存在没有下标的行,因此具有无损连接。
检验依赖保持:
{A,B} : A → B
{B,C} : B → C
丢失了C → A信息,依赖不能保持,因此选择B。
例题3:
Consider a relation schema R
F={AB → CD,B → D,C → E,CE → B,AC → B}.
(1)Use Armstrong axioms and related rules to proof the functional dependency AC->E.
(2)Find a canonical cover Fc of F, and compute {C}+ .
(3)Find all candidate keys, and point out R is in which normal form.
(4)Decompose R into 3NF that is dependency preserving and lossless-join.
(5)Explain or demonstrate that your decomposition is dependency preserving and lossless-join.
解答:
已知 R(A,B,C,D,E) : AB → CD , B → D , C → E , CE → B , AC → B 。
(1)用Armstrong axioms规则推导出AC->E。
增长律Augmentation:if A->B then AC->BC,这个比较重要,延长函数依赖不变。
我们这样推导,C->E then AC->AE then AC->E(分解/结合规则)推导结束。
(2)canonical cover即依赖的最小覆盖,其实就是求最小化基本集。
在二.7中已经给出过程,最后得到以下结果:
AB → C , B → D , C → E , C → B 。
该问题后面需要求{C}+ ={C,E,B,D},可以用上面得到的最小化基本集来解,减少了一些不必要的过程。
(3)找到所有候选键,并指出关系R是属于何种范式。
二.6中已经给出过程,结果如下:
候选键:{A,B}、{A,C}
主属性:A,B,C
非主属性:D,E
函数依赖:AB → C,B → D,C → E,C → B
对于第二范式,非主属性D、E由键的一部分决定,不满足,因此为第一范式
(4)将该关系分解为满足第三范式的关系。
{A,B,C,D,E} : AB → C , B → D , C → E , C → B,候选键: {A,B}、{A,C}
<1>——分解为第二范式
{A,B,C,E} : AB → C , C → E , C → B, 候选键:{A,B}、{A,C}, 主属性:A,B,C, 非主属性:E。
由于AB → C → E满足第二范式。
{B,D} : B → D, 候选键:{B} , 主属性:B , 非主属性:D
由于D由键决定,满足第二范式。
<2>——再分解为第三范式
对于{A,B,C,E}由于存在非主属性E对于键AB的传递依赖,不满足第三范式,继续分解。
{A,B,C} : AB → C , C → B , 候选键:{A,B}、{A,C}, 主属性:A,B,C, 非主属性:无
没有非主属性,满足第三范式。
{C,E} : C → E , 候选键:{C},主属性:C,非主属性:E
由于E直接由键决定且无传递依赖,满足第三范式
对于{B,D}没有非主属性对于键的部分、传递依赖,也满足第三范式。
因此,最后分解为:
{A,B,C} : AB → C , C → B
{C,E} : C → E
{B,D} : B → D
(5)证明这个划分是无损连接。
用chase检验:
<1>——用划分集合初始化表
<2>——逐一根据函数依赖更改表中值(优先选择无下标的),得到如下图
<3>判断是否存在全部不带下标的行
存在,因此具有无损连接。