STL——概述

注：本文主要参考自《STL 源码剖析》，故涉及到的文件及源码均基于SGI STL(GCC采用)

一、STL六大组件

---

1、容器（containers）：STL内部封装好的数据结构，一种class template，常用的包括vector、list、deque、set、map、multiset、multimap等
2、算法（algorithm）：一种function template，常用的有sort、search、copy、erase等
3、迭代器(iterator)：泛型指针，是一种智能指针，是一种将operator*，operator->，operator++，operator–等指针相关操作予以重载的class template。所有STL容器都附带自己的迭代器
4、仿函数(functor)：行为类似函数，就是使一个类的使用看上去象一个函数，具有可配接性。它的具体实现就是通过在类中重载了operator()，使这个类具有了类似函数的行为，就是一个仿函数类了。一般函数指针、回调函数可视为狭义的仿函数。以操作数的个数划分，可分为一元和二元仿函数；以功能划分，可分为算术运算、关系运算、逻辑运算三大类。这部分内建的仿函数，均放在头文件里，使用时需引入头文件
STL内建仿函数分类包括：
  1）算术类仿函数
     加：plus
     减：minus
     乘：multiplies
     除：divides
     模取：modulus
     否定：negate
  2）关系运算类仿函数
     等于：equal_to
     不等于：not_equal_to
     大于：greater
     大于等于：greater_equal
     小于：less
     小于等于：less_equal
  3）逻辑运算仿函数
     逻辑与：logical_and
     逻辑或：logical_or
     逻辑否：logical_no
使用举例如下：

#include   
#include   
#include    
#include    
using namespace std;  

int main()  
{  
    int ia[]={1,2,3,4,5};  
    vector<int> iv(ia,ia+5);  
    cout<1,multiplies<int>())<int> multipliesobj;
    cout<3,5)<int>());    
    modulus<int>  modulusObj;  
    cout<3,5)<// 3   
    return 0;   
}   

5、配接器(adapter)：一种用来修饰容器(container)或仿函数(functor)或迭代器(iterator)接口的东西。如queue和stack。它们的底部完全借助deque，所有操作都由底层的deque供应。改变functor接口者，称为functor adapter，改变container接口者，称为container adapter；改变iterator接口者，称为iterator adapter。
6、配置器(allocator)：负责空间配置与管理。是一个实现了动态空间配置、空间管理、空间释放的class template。一般SGI STL为每一个容器都指定其缺省的空间配置器为alloc（SGI配置器）

二、从配置器剖析STL内存机制

---

一般而言，我们习惯的C++内存配置操作和释放操作是这样的：

class Foo {...};
Foo *pf = new Foo;
delete pf;

这其中的new算式内含两阶段操作：
     （1）调用::operator new配置内存；
     （2）调用Foo::Foo() 构造对象内容
delete算式也内含两阶段操作：
     （1）调用Foo::~Foo()析构对象内容
     （2）调用::operator delete释放内存

STL allocator将这两阶段操作区分开来，内存配置由alloc::allocate()负责，内存释放操作由alloc::deallocate()负责，存放在中；对象构造操作由::construct()负责，对象析构操作由::destroy()负责，定义在中，整个配置器定义于之中

其中，构造、析构函数被设计为全局函数，同时，配置器中也必须拥有construct()和destroy()两个成员函数，具体实现也不算复杂，看过源码之后应该大概可以理解，只是根据不同的情况重载了几个版本，这里不做重点讨论，下面就空间的配置与释放进行详细展开。

首先我们要先了解SGI设计alloc时的几个基准：
（1）需要实现向系统堆栈申请空间
（2）考虑多线程状态
（3）考虑内存不足时的应变策略
（4）考虑过多“小型区块”可能造成的内存碎片问题
内存的配置：
首先是申请内存空间的问题，SGI中使用malloc()和free()完成内存的配置与释放；考虑到内存碎片的问题，SGI设计了双层级配置器来解决这一问题

所谓的双层级配置器，即设计了第一级配置器和第二级配置器以应对不同的内存需求。
第一级配置器直接使用malloc()和free()，realloc(),并实现出类似C++ new-handler机制。所谓的C++ new-handler机制，即指可以要求系统在内存配置需求无法满足时，调用一个你所指定的函数（由客端提供）。对于::operator new来说，指定的函数即被称为new-handler，它对解决内存不足有一个特定的模式。这里因为没有使用::operator new，所以没有直接运用该机制，而是仿写了一个类似的set_malloc_handler()。若内存不足处理例程未被客端设定，则SGI一级配置器会直接调用_THROW_BAD_ALLOC，丢出bad_alloc异常信息，或利用exit(1)硬生生终止程序。
至于为什么SGI没有采用::operator new来配置内存，《STL 源码剖析》认为除了历史因素之外，可能是由于C++未提供realloc()的内存配置操作。

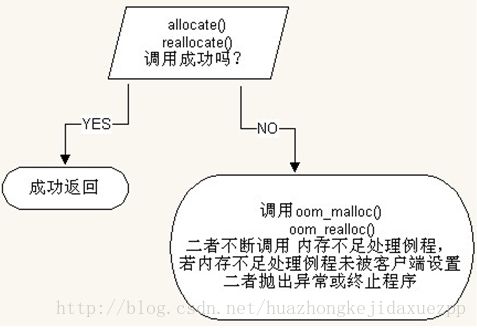
第二级配置器不同情况下采用不同的策略：（1）当申请的内存空间（我们视为配置区块）超过128字节时，视为“足够大”的内存空间，可以直接分配内存，即调用第一级配置器；（2）当申请的内存空间小于128字节时，考虑到小额内存的分配成本以及内存碎片等问题，为了降低额外负担，采用复杂的内存池（memory pool）的整理方式

下面详细介绍一下内存池管理：此法又称为次层配置：（暂时借用一下别人的图，之后有时间补上）
对于小额区块的内存需求量，判断freelist是否有直接可用的区块，有，则直接分配；没有，就需要为free-list重新分配空间：先将所需内存先上调至8的倍数（为方便管理），调用refill()，先从内存池中取出新的空间（用chunk_alloc()实现），缺省取得20个新区块，若内存池空间不足以提供20个区块（或指定区块数），但足够供应一个及以上的区块，就将所能提供的所有区块均提供出去；若内存池连一个区块空间都无法供应，此时便需要利用malloc()从heap中重新配置内存，为内存池提供内存空间。重新分配的内存大小一般为需求量（默认节点数为20）的两倍，再加上一个随着配置次数增加而增加的附加量。维护的对应的自由链表（free-list，一般维护16个，各自管理大小分别为8,16,24,32,48,56,64,72,80,88,96,104,112,120,128字节）
——>若system heap中没有足够的内存可供分配，则查找free_list其他区块，是否有未释放的空间，若有未使用的足够大的区块，若有，则分配给客端；若没有，则调用第一级配置器，虽然也是用malloc进行内存分配，但由于第一级配置器具有out-of-memory机制（类似new-handler机制），调用客端设定的内存不足处理例程，看能否从其他进程获取释放的内存，若可以，则成功；若失败，则返回bad_alloc异常
——>如果客端释放了使用的小额区块，就由配置器回收到自由链表中。

自由链表的节点结构如下：

union obj{
    union obj *free_list_link;
    char client_data[1];
};

一个能详细阐述上述过程的例子，如下所示：

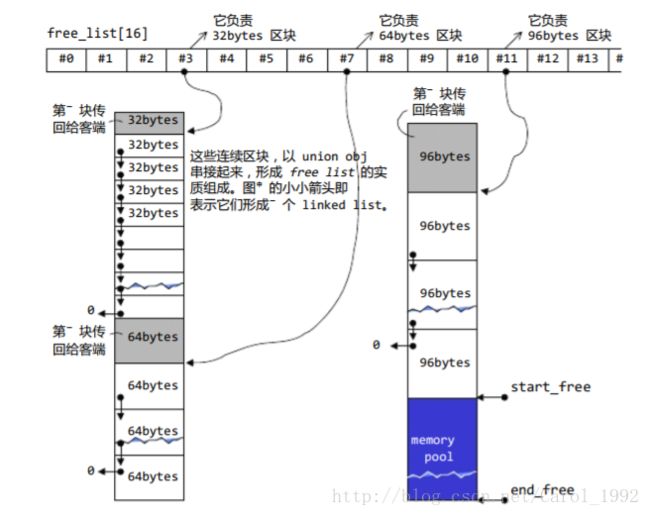
  上图中，假设程序一开始，客端就调用 chunk_alloc(32,20)，于是malloc() 配置2*20 个 32bytes 区块，其中第 1 个交出，另 19 个交给 free_list[3]维 护 ， 余 20 个留给记忆池 。 接 下来客端调用 chunk_alloc(64,20) ， 此时free_list[7] 空空如也，必须向内存池要求支持。内存池只够供应 (32*20)/64=10个 64bytes 区块，就把这 10 个区块返回，第 1 个交给客端，余 9 个由 free_list[7]维护。此时内存池全空。接下来再调用 chunk_alloc(96, 20)，此时free_list[11]空空如也，必须向内存池要求支持，而内存池此时也是空的，于是以 malloc() 配置 40+n（附加量）个 96bytes 区块，其中第 1 个交出，另 19 个交给 free_list[11]维护，余 20+n（附加量）个区块留给内存池……
   如果整个 system heap 空间都不够了（以至无法为内存池注入活水源头），malloc() 行动失败，chunk_alloc() 就四处寻找有无「尚有未用区块，且区块够大」之 free lists。找到的话就挖一块交出，找不到的话就调用第一级配置器。第一级配置器虽然也是使用 malloc() 来配置内存，但它有 out-of-memory处理机制（类似 new-handler 机制），或许有机会释放其它的内存拿来此处使用。如果可以，就成功，否则发出 bad_alloc 异常。

注意：配置器不仅负责分配内存，还负责回收内存

注意：是否使用第二级配置器可以通过定义_USE_MALLOC条件编译实现（SGI STL默认没有定义），其中，_malloc_alloc_template是第一级配置器，_default_alloc_template是第二级配置器;
在SGI STL中，为了使配置器的接口能够符合STL规格，SGI将alloc包装在一个接口——simple_alloc中，接口内部实现将调用传递给配置器的成员函数，同时使配置器的配置单位从bytes转为个别元素的大小（利用sizeof(T)）。SGI STL容器全都使用这个simple_alloc接口

内存的释放：
_default_alloc_template配置器拥有配置器标准接口函数deallocate()。该函数首先判断区块大小，大于128字节就调用第一级配置器，小于128字节就找出对应的free_list，将区块回收

三、常用容器

---

序列式容器：

1、vector
vector与数组类似，维护一个连续线性空间，支持随机存取，不同点是其是动态空间，随着元素的加入，它的内部机制会自行扩充空间以容纳新元素。其迭代器是普通指针，它以两个迭代器start和finish分别指向配置得来的连续空间中目前已被使用的范围，并以迭代器end_of_storage指向整块连续空间（含备用空间）的尾端
为了降低空间配置时的速度成本，vector实际配置的大小可能比客户端需求量更大一些——capacity，这里缺省采用前述的alloc空间配置器，同时据此另外定义了一个data_allocator，以方便以元素大小为配置单位：typedef simple_alloc data_allocator

vector内存分配实现：
当push_back(x)将新元素插入vector尾端时，该函数首先检查是否还有备用空间，如果有就直接在备用空间上构造元素，并调整迭代器finish；如果没有，就扩充空间（重新配置、移动数据、释放原空间）：
调用data_allocator::allocator重新配置一块大小为原空间两倍大小（若原空间为0，则新空间配置为1）的新内存空间
——>调用uninitialized_copy将原vector的内容拷贝到新vector中，并对新元素设定初值x
——>析构并释放原vector（destroy,deallocate）
——>调整迭代器指向新的vector
由上述过程可知，针对vector的任何操作，一旦引起空间重新配置，指向原vector的所有迭代器就都失效了

2、list
双向链表，每次插入或删除一个元素，就配置或释放一个元素空间。因此，对空间运用精准，不存在浪费。对任何位置的元素插入或元素移除，时间复杂度为常数。
插入和接合(splice）操作都不会造成原有的list迭代器失效，删除操作只是使“指向被删除元素“的迭代器失效，其它迭代器不受影响。
SGI list是环状双向链表，在尾端刻意放置一个空白节点，则只需要一个指针指向该节点，便可表示整个链表，同时符合STL对于“前闭后开“区间的要求，称为last迭代器。
如：iterator begin(){return (link_type)((*node).next);}
iterator end(){return node;}

list缺省采用alloc空间配置器，同时据此另外定义了一个list_node_allocator，以方便以节点大小为配置单位
push_back()函数内部调用insert()（有多个重载形式）实现
list内部还提供了一个所谓的迁移操作(transfer，非公开)，将某连续范围的元素迁移到某个特定位置之前，该操作为其他的复杂操作如splice,sort,merge等奠定良好的基础
list不能使用STL的sort算法，必须使用自己的sort()，因为STL算法中的sort()只接受随机存取的迭代器

3、deque：
deque是一种双向开口的连续线性空间，仅可以在头尾两端分别作元素的插入和删除操作。可以遍历。

deque和vector的差异在于：
（1）deque允许于常数时间内对起头端进行元素的插入或移除操作；
（2）deque没有所谓容量capacity观念，因为它是动态地以分段连续空间组合而成，随时可以增加一段新的空间并连接起来。因此，deque也没有必要提供空间保留(reserve)功能。
（3）deque的迭代器虽然是随机存取迭代器，并非普通指针，复杂度较高，因此一般建议选择vector而非deque，若对deque进行排序，最高效率的方式是把deque先完整复制到一个vector身上，将vector排序后，再复制回deque

deque内部实现：
deque采用一块map（不同于STL的map，这里的map是一小块连续空间，类似于vector，也是一个指针）作为主控，其中的每个元素（每个节点）指向另一大块连续线性空间，称为缓冲区（默认大小为512字节）。缓冲区是deque真正用来存放数据的地方。
当map使用率使用率满载，便需要再找一块更大的空间来作为map。配置策略见reallocate_map()
由上可以看出，deque是将vector和list结合起来实现，即将分段连续空间用链表的方式连接起来
，它的iterator需要包含first指针（指向当前缓冲区的头）,last（指向当前缓冲区的尾），cur（指向当前缓冲区的现行元素），node（指向管控中心map的指针）

class deque{
public:
    typedef _deque_iterator iterator;
protected:
    iterator start;   //指向第一个缓冲区的第一个元素
    iterator finish;  //指向最后一个缓冲区的最后一个元素（的下一个位置）
    value_type** map;   //指向map
    size_t map_size;    //map内有多少指针
};

何时需要配置新缓冲区？
当当前最后一个缓冲区只剩一个元素备用空间或者当前第一个缓冲区没有任何备用元素时才会被调用，前者调用push_back_aux，后者调用push_front_aux
利用reserve_map_at_back()和reserve_map_at_front()来判断什么时候map需要重新整治，map分配新的空间是用reallocate_map（配置一块新空间，把原map内容拷贝过来，释放原map，设定新map的起始地址与大小，重新设定迭代器start和finish）实现的
pop_front()和pop_back()需要考虑和释放缓冲区
因为deque最初状态需要保有一个缓冲区，因此，clear()完成之后恢复初始状态，也要保留一个缓冲区

4、stack
stack不属于容器，属于配接器（修改某物接口，使其符合一定的特性），但由于使用起来与容器相似，因此在这里暂时把它算为容器进行整理。
它是一种先进后出的数据结构，只有最顶端一个出口。因此，不具有遍历行为。
缺省以deque作为底部结构并封闭其头端开口，不提供随机访问功能，也不提供迭代器。
注：list也是双向开口的数据结构，且在stack内部实现过程中用到的所有函数list均具备，因此list也可以形成stack，使用方式如下：

stack<int,list<int>> istack;

5、queue
一种先进先出的数据结构，它有两个出口。但仅允许从最底端加入元素、最顶端取出元素；同时不允许遍历。
同stack一样，属于配接器。缺省情况下将deque作为底部结构。不提供迭代器。同上，也可以用list实现queue的功能。

6、heap(可定义元素大小比较标准)
heap不属于STL组件，一般以算法形式呈现它充当priority queue的助手。priority queue底层结构用的是二叉堆（完全二叉树），借用数组array可实现二叉树的表达——隐式表述法。但为了实现动态改变，以vector代替array。不提供遍历功能，也不提供迭代器。
STL中提供的priority queue默认是大根堆

heap相关算法：
push_heap()：新加入的元素放在最后一个叶节点处，再根据当前是大根堆还是小根堆对堆进行调整（_adjust_heap()，执行percolate up上溯程序，将新节点与父节点进行比较，若其键值比父节点大/小，则交换两者的位置，一直到不需兑换或者直到根节点为止）
pop_heap()：取走根节点之后，割舍最下层最右边的叶节点，先执行下溯程序：将去掉根节点之后的空结点和其较大子节点“对调”，并持续下放，直至叶节点为止。然后将前述割舍的叶节点的元素值设给这个“已到达叶层的空洞节点”，再对它执行一次上溯程序。
注意：pop_heap之后，最大元素只是被置于底部容器的最尾端，尚未被取走。如要取其值，可使用底部容器所提供的back()，如果要移除它，可使用pop_vack()
sort_heap()：持续对整个heap做pop_heap操作，每次将操作范围从后向前缩减一个元素，便可得到一个递增序列
注意：排序过后，原来的heap就不再是一个合法的heap了
make_heap()：这个算法用来将一段现有的数据转化为一个heap，循环调用_adjust_heap()
示例：

int ia[9]={0,1,2,3,4,5,6,7,8};
vector<int> ivec(ia,ia+9);

make_heap(ivec.begin(),ivec.end());

ivec.push_back(10);
push_heap(ivec.begin(),ivec.end());

pop_heap(ivec.begin(),ivec.end());
cout<

7、priority_queue
是一个拥有权值观念的queue，同样只允许在底端加入元素，并从顶端取出元素
缺省情况下基于max_heap（以vector作为底部容器）完成，权值最高者，排在最前面（递减）。同样被归为配接器。可定义元素大小比较标准。没有迭代器，也不能遍历。

关联式容器：

标准的分为set（集合）和map（映射表）两大类，均是基于RB-tree（一种平衡二叉树）实现；此外，还提供了hash table（散列表），基于此完成的hash_set、hash_map、hash_multiset、hash-multimap等
每个数据元素都有一个键值(key)和一个实值(value)。没有所谓的头尾（只有最大元素、最小元素），所以没有push_back()、push_front()、pop_back()、pop_front()、begin()、end()等操作。
面对关联式容器，应该使用其所提供的find函数来搜寻元素，会比使用STL算法find()更有效率。

8、set：
以红黑树为底层机制。

RB-tree迭代器实现分为两层，与slist类似。RB-tree迭代器属于双向迭代器，但不具备随机定位能力，其提领操作和成员访问操作与list十分近似，较为特殊的是其前进和后退操作。其前进操作operator++()调用了基层迭代器的increment()，后退操作operator–()则调用了基层迭代器的decrement()，前进或后退的举止行为完全依据二叉搜索树的节点排列法则。

set所有元素都会根据元素的键值自动被排序。其键值即为实值，不像map同时拥有实值和键值，所以set**不允许两个元素有相同的键值（它的插入操作采用的是底层机制RB-tree的insert_unique()），相同的值不会被存入，也不能通过set的迭代器改变set的元素值**，因为set元素是其键值，关系到set元素的排列规则。如果任意改变set元素值，会严重破坏set组织。set源码中迭代器被定义为底层RB-tree的const_iterator，杜绝写入操作）

与list相同。当客户端对它进行元素新增操作或删除操作时，操作之前的所有迭代器，在操作完成之后都依然有效（除了被删除元素的迭代器），因为set和list相似，没有vector那样 分配新内存——将原内存的内容复制到新内存——释放旧内存的过程。

定义形式：

int ia[5] = {0,1,2,3,4};
set<int> iset(ia,ia+5);

9、map：
以红黑树为底层机制。
map所有元素都会根据元素的键值自动被排序。map的所有元素都是pair，同时拥有实值value和键值key。可表示为pair。map同样不允许两个元素有相同的键值（它的插入操作采用的是底层机制RB-tree的insert_unique()），相同键值的元素插入不会被覆盖，若想键值不唯一，可使用multimap。

不能通过map的迭代器改变map元素的键值，因为map元素的键值，关系到map元素的排列规则。如果任意改变map元素键值，会严重破坏map组织。但可以修正元素的实值。因此，map源码中迭代器既不是一种constant iterator，也不是一种mutable iterators。

与list相同。当客户端对它进行元素新增操作或删除操作时，操作之前的所有迭代器，在操作完成之后都依然有效（除了被删除元素的迭代器）。

定义形式：

map<string,int> simap;
simap[string("jihou")] = 1;
simap[string("jerry")] = 2;
simap[string("jason")] = 3;
simap[string("jimmy")] = 4;

pair<string,int> value(string("david"),5);
simap.insert(value);

[]操作符如simap[string(“jihou”)]既可以做左值，又可以做右值。如
int number = simap[string(“jihou”)];
因此operator[]的返回值为引用，具体代码如下：

T& operator[](const key_type& k) {
    return (*((insert(value_type(k,T()))).first)).second;
}

10、multiset
multiset特性与用法和set完全相同，唯一差别在于它允许键值重复，因此它的插入操作采用的是底层机制RB-tree的insert_equal()而非insert_unique()。

11、multimap
multimap特性与用法和set完全相同，唯一差别在于它允许键值重复，因此它的插入操作采用的是底层机制RB-tree的insert_equal()而非insert_unique()。

12、hashtable
hashtable可提供对任何有名项的存取操作和删除操作。由于操作对象是有名项，所以hashtable也可被视为一种字典结构。这种结构的用意在于提供常数时间之基本操作。

他的实现主要基于两个部分：构造哈希函数和解决冲突碰撞，具体内容可参考 数据结构之（一）Hash（散列）

SGI STL的 hash table采用拉链法解决冲突，它的主哈希表使用vector实现的（命名为buckets，以便有动态扩充能力，表格大小最好为质数），各节点对应的list不是采用的STL的lsit或slist，而是自行维护hash table node（构造hash table时，先确定与所给大小最接近的大于或等于的质数，然后创建该质数个元素空间大小的buckets vector空间，并设定所有buckets的初值为0）

template<class Value>
struct __hashtable_node
{
    __hashtable_node* next;
    Value val;
};

注意：hashtable的迭代器没有后退操作，也没有定义所谓的逆向迭代器

hashtable插入元素的过程：
找指定书目最近的最小质数，保留对应个数的buckets vector，每个buckets（指针，指向一个hash table节点）的初值为0.接下来正常插入元素。当插入元素个数超过当前buckets vector的大小，符合表格重建条件（这部分在resize()中实现），于是，设立新的buckets，处理每一个旧bucket所含（串行）的每一个节点，找出节点落在哪一个新bucket内，令旧bucket指向其对应之串行的下一个节点，将当前节点插入到新bucket内，成为其对应串行的第一个节点，再回到旧bucket所指的待处理串行，准备处理下一个节点。直至所有节点处理完毕，对调新旧两个buckets，释放对调后的新bucket内存
具体例子如下：

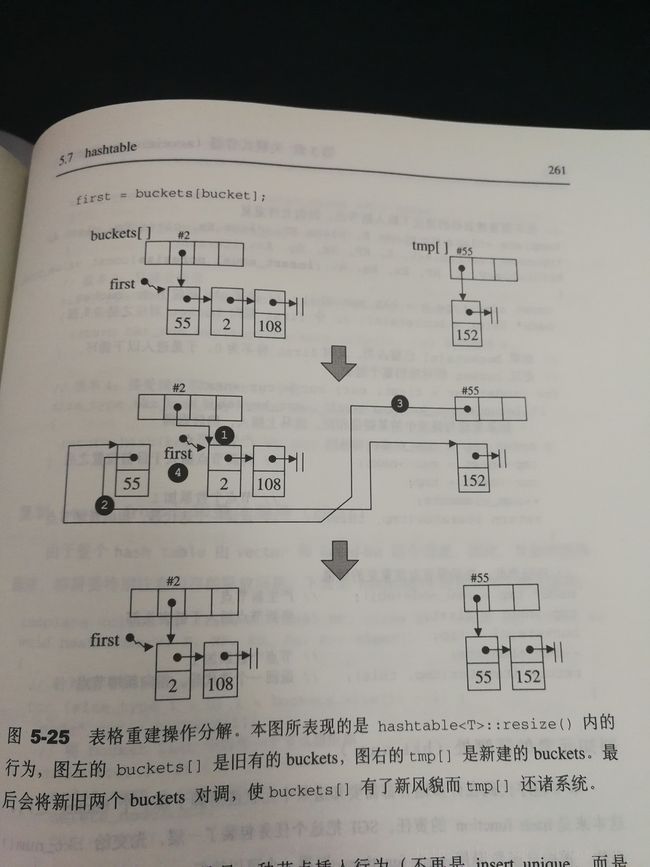
这里比较疑惑的一点是为什么一开始要确定node节点的个数，从链表的角度来考虑，每次插入一个元素，就直接链接一个Node节点即可就好了，后来和朋友讨论之后，猜测是为了效率的原因，一次分配较大内存，避免了添加一个元素，分配一个内存所消耗的时间成本，类似内存池的机制考虑，我想这也是为什么hash table内部实现没有采用list的原因吧。
此外，从上述过程分析可知，不论删除还是插入，迭代器均不会失效（因为内存交换之后，实际内存中的元素没有变？？）

hashtable默认处理型别包括short,int,unsigned short,unsigned int,long,unsigned long，插入，unsigned char,signed char等，除此之外的如string,double,float等均不能直接处理，若想处理这些型别，用户必须自行为它们定义hash function。hash_set、hash_map、hash_multiset、hash_multimap等同理。

注：除了下面提到的hash_set、hash_map、hash_multiset、hash_multimap等，unordered_set、unordered_map、unordered_multiset、unordered_multimap也是基于hashtable构建的容器，且在C++11的时候被引入标准库了，而hash_set、hash_map、hash_multiset、hash_multimap等并没有，所以一般建议使用unordered_set、unordered_map系列比较好。此外，Visual Studio（当然需要支持c++11的版本）库中两个数据结构都有定义，而在gcc/g++中并不支持hash_set、hash_map等。

13、hash_set
以hashtable为底层机制。但没有自动排序功能。除此之外，使用方式与set完全相同

14、hash_map
以hashtable为底层机制。但没有自动排序功能。除此之外，使用方式与map完全相同

15、hash_multiset
hash_multiset的特性与multiset完全相同，唯一差别是以hashtable作为底层机制。因此，hash_multiset也不会自动排序。
与hash_set的差别是插入操作采用的是底层机制hashtable的insert_equal()而非insert_unique()。

15、hash_multimap
hash_multimap的特性与multimap完全相同，唯一差别是以hashtable作为底层机制。因此，hash_multimap也不会自动排序。
与hash_map的差别是插入操作采用的是底层机制hashtable的insert_equal()而非insert_unique()。

---

附：
面试中常常会问到set、hash_set等的比较问题，这里做一个小的总结

set/map与hash_set/hash_map的比较：

1. 两者底层实现不同：set/map基于红黑树,hash_set/hash_map基于hash表，所以set/map的查找、删除、插入平均和最坏都是对数时间效率，而hash_set/hash_map查找、插入、删除一般是O（1），但是最坏也可达O（N）,因而不能认为hash_set/hash_map的查找实践一定比map短，这要综合数据量等多方面因素来考虑

2. set/map空间消耗比hash_set/hash_map少，因为红黑树占用的内存更小（仅需要为其存在的节点分配内存），而Hash事先就应该分配足够的内存存储散列表（即使有些槽可能遭弃用）。因此对于内存限制较高的情况，选用set/map要优于hash_set/hash_map

3. set/map是自排序的，而hash_set/hash_map是无序的

对于set/map来说，为什么选用红黑树而不用AVL树呢？

1. 单从查找、删除、插入等的时间复杂度来看，两者旗鼓相当，但因为AVL树对平衡条件要求更为严格，因此当进行操作时，AVL树进行调整的频率与次数要比红黑树高，也因此对于数据量较大插入或删除时或者数据复杂的情况，红黑树需要通过旋转变色操作来重新达到平衡的频度要小于AVL，因此红黑树比AVL(平衡二叉搜索树)具有更高的插入效率，虽然查找效率会平衡二叉树稍微低一点点，但是这种查找效率的损失是非常值得的。它的操作有着良好的最坏情况运行时间，并且在实践中是高效的: 它可以在O(log n)时间内做查找，插入和删除。

2. 此外，需要平衡处理时。红黑树比AVL树多一种变色操作，而且变色的时间复杂度在对数量级上，但因为操作相对简单，所以在实际应用中，这种变色仍然十分快速，对效率影响较小

3. 当插入一个节点引起树的不平衡时，AVL和红黑树都最多需要2次旋转操作。但删除一个节点引起不平衡之后，AVL最多需要logN次旋转操作，而红黑树最多只需要3次。任何不平衡都会在3次旋转之内解决。因此两者插入一个结点的代价差不多，但删除一个结点的代价红黑树要低一些。

4. AVL和红黑树的插入删除代价主要还是消耗在查找待操作的结点上。因此时间复杂度基本上都是与O(logN) 成正比的。

总体评价：大量数据实践证明，RBT的总体统计性能要好于平衡二叉树。