libigl cot laplace 计算方式

速记一下

基本概念

https://blog.csdn.net/hjimce/article/details/46415239

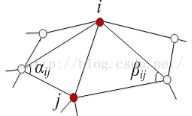
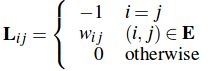
libigl 计算方式

因为 cot = cos / sin,
cos 可以用余弦定理

sin 用向量叉积 $|a||b|sin\theta$ , 和面积有关
因此发现计算出每条边的长度的平方和区域的面积就好办了. ligigl 就是这么做的

主程序在, 关注sample_size=3 这个分支:
https://github.com/libigl/libigl/blob/master/include/igl/cotmatrix_entries.cpp

算长度平方: https://github.com/libigl/libigl/blob/master/include/igl/squared_edge_lengths.cpp

igl::squared_edge_lengths(V,F,l2);

算面积 https://github.com/libigl/libigl/blob/master/include/igl/doublearea.cpp

//doublearea(l,0.,dblA);

const Scalar arg =
        (l(i,0)+(l(i,1)+l(i,2)))*
        (l(i,2)-(l(i,0)-l(i,1)))*
        (l(i,2)+(l(i,0)-l(i,1)))*
        (l(i,0)+(l(i,1)-l(i,2)));
      dblA(i) = 2.0*0.25*sqrt(arg);

应该是类似这个公式
https://en.wikipedia.org/wiki/Heron%27s_formula
$A=\frac{1}{4}\sqrt{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}$

发现L 是 按照主对角线是负数的

int source = F(i,edges(e,0));
      int dest = F(i,edges(e,1));
      IJV.push_back(Triplet(source,dest,C(i,e)));
      IJV.push_back(Triplet(dest,source,C(i,e)));
      IJV.push_back(Triplet(source,source,-C(i,e)));
      IJV.push_back(Triplet(dest,dest,-C(i,e)));