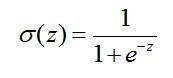机器学习笔记1：基于Logistic回归进行数据预测

机器学习笔记1：基于Logistic回归进行数据预测

一、背景

　　
　　近期项目的一个核心部分就是实现对数据的预测，因为没有实际的数据样本，所以我准备近期学习Machine Learning的几种方式，从简单的线性非线性回归到TensorFlow及其他几种深度学习的方式，搭建相关的数据预测核心部分，并且完成各个系统的测试。等到实际数据获取后，进行系统测试与比对，选择最适合数据预测的类型。
　　
　　因为Machine Learning涉及到很多数学相关的知识，因此在基础知识方面，我看的是Coursera中的斯坦福大学的Machine Learning的网课。在实际操作的过程中参考Peter Harrington的《机器学习实战》一书，但是本书在深度学习方面没有相关的章节，因此我会从CSDN中找到合适的学习资源进行学习与更新。

二、基础知识

1.logistic回归介绍

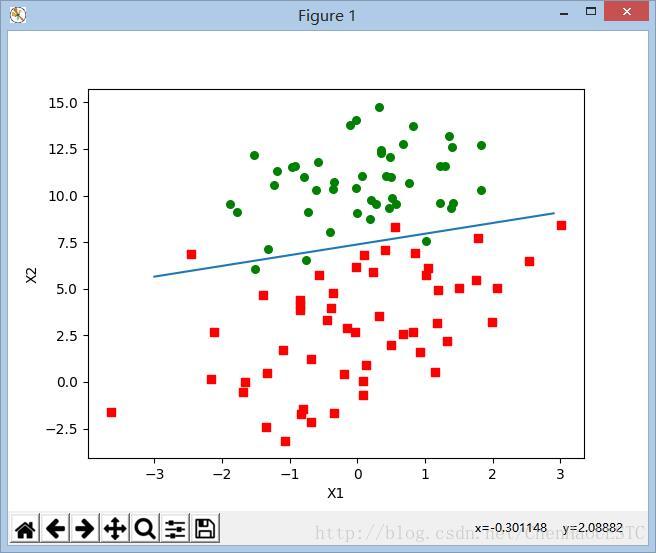
　　Logistic回归也就是逻辑回归，在下面的这个例子中，就是找到一条拟合的直线，将两类数据分开，下面的例子就是采用二维的数据，用一条直线将绿点和红点分开。

2.Logistic公式原理

　　关于这条直线，我们可以用下面的公式来表现：
　　

3.算法步骤

(1)算法的第一步就是实现数据的初始化，将二维的数据转换为三维的数据，上面提到便于计算将x0设置为1，因此可以人为的将其转换为三维数组。
(2)首先对参量w进行初始化为n行1列的单元数组。
(3)根据实际情况通过梯度下降方式，取得直线上拟合值与真实值之差的最小值，通过多次迭代的方式来求出最优的w值。
(4)经过迭代后获得w值，做出拟合直线，用X2表示纵坐标，作出直线，观察效果。

4.梯度算法

5.梯度下降算法应用

　　关于参数w的迭代方程的推导过程如下：

(1)在测试的过程中，在构建误差函数的时候，采用最小二乘法，用分类误差评估分类的效果。其中label就是数据集的第三列数据，将x与m的乘积采用sigmoid函数处理。

(2)想要w值达到达到最小值，可以参考Coursera里面的课程内容，如图所示，如何到达最小值的点，需要一步步来进行迭代更新，在每一步求导，找到该点能够得到最小值的方向。所以算法的第二步就是进行求导运算。

求导过程如下：

6.处理数据中的缺失值

(1)使用可用特征的均值来填补缺失值；
(2)使用特殊值来填补缺失值，如-1；
(3)忽略有缺失的样本；
(4)使用相似样本的均值填补缺失值；
(5)使用另外的机器学习的算法预测缺失值。

三、代码部分

　　这个部分会尽量对整个项目的每个函数给出解释，同时书中的source code关于梯度上升的算法，给出了一种基本算法以及两种改进方式，会在下面部分有所解释。完整的代码段及数据可以在第四部分中下载得到。

(1)导入数据

def loadDataset():
    dataSet = []  # 数据集
    labels = []  # 标签
    fr = open("testSet.txt")
    for line in fr.readlines():
        lineVec = line.strip().split()  # 读取每一行,[x1,x2,label]
        # [x0,x1,x2]，其中x0表示常数项
        dataSet.append([1.0, float(lineVec[0]), float(lineVec[1])])
        labels.append(float(lineVec[2]))  # 添加标签
    return dataSet, labels  # 返回读取的数据集，及标签

　　将数据集与代码放在同一个文件夹下，就可以直接使用open指令将其打开，同时读取每一行的数据，并且对每一行的三列数据进行分离，将其转换为数组存入lineVec变量中，然后将每一行的前两列数据加上一列1，将数据依次存入到dataSet的矩阵中。将第三列的数据存入label的矩阵中，代表每个数据的标签。然后返回dataSet与labels这两个矩阵。

(2)Sigmoid函数

def sigmoid(xVec):  # 根据输入数据的类型分开处理
    if np.array(xVec).shape == np.array(0).shape:  # 如果输入为一个数值
        if xVec > 100:  # 防止数据计算溢出
            xVec = 100
        if xVec < -100:  # 防止数据计算溢出
            xVec = -100
        return 1.0 / (1 + math.exp(-xVec))
    else:  # 数组
        ret = []
        for x in xVec:
            x1 = x
            if x1 > 100:  # 防止数据计算溢出
                x1 = 100
            if x1 < -100:  # 防止数据计算溢出
                x1 = -100
            ret.append(1.0 / (1 + math.exp(-x1)))
        return ret

　　对于Sigmoid的计算，分为两种形式，当输入的只是数字的时候，直接带入公式计算，当输入的是数组的形式，则将其中的每个元素挑出来计算，完成后再将其以数组的形式保存。其中对数据取-100到100区间的计算，我认为是计算的过程涉及到指数函数，如果输入的x过大，在sigmoid函数中一定是作为1或者0，继续计算的话反而会增加系统的运算量，导致数据计算溢出。因此在此设置-100到100之间的阈值，超过则作超过处理。

(3)Logitic回归梯度上升算法

def gradAscent(dataSet, label):
    dataSet = np.mat(dataSet)  # list转换为array
    label = np.array(label).T  # list转换为array并进行转置
    label = mat(label)
    m, n = dataSet.shape  # m参与训练数据集数，n表示每组的维度
    alpha = 0.02  # 调整参数
    maxCycles = 1000  # 训练的迭代的次数
    weights = np.ones((n, 1))  # 初始权值都为1
    weights = mat(weights)
    for i in range(maxCycles):  # 迭代求weights
        h = sigmoid(dataSet * weights)
        error = label - h  # 差
        weights = weights + alpha * (dataSet.T * error.T)  # 更新权值
    return weights

　　Logistic基础算法部分如上，首先将获取到的数据由Array转换为Matrix格式，Matrix专门用来进行线性代数的操作，对于label参量，首先要进行转置，由n行1列转置为1行n列，然后设定迭代的次数以及调整的参数，将weights的初始权值都设为1，进行算法的迭代。最终根据各个参数收敛的情况来判定其效果。

(4)随机梯度上升算法

def randGradAscent(dataSet, label, numIter=89):
    dataSet = np.array(dataSet)  # list转换为array
    label = np.array(label).T  # list转换为array
    m, n = dataSet.shape  # m参与训练数据集数，n表示每组的维度
    alpha = 0.01  # 学习速率
    weights = np.ones((n, 1))  # 初始权值都为1
    for j in range(numIter):
        for i in range(m):  # 迭代m次，求weights
            h = sigmoid(sum(dataSet[i] * weights))
            error = label[i] - h  # 差
            weights = weights + alpha * error * dataSet[i]  # 更新权值
    return weights

　　梯度上升算法在更新回归系数时，都需要遍历整个数据集，这种方法在处理100个左右的数据集时候还可以，但是如果有数十亿的样本和大量的特征时，这样的算法复杂度就太高。而随机梯度上升算法作为一种改进，一次仅用一个样本点来更新回归系数。随机梯度上升算法和梯度上升算法在代码上看起来很一致，但是有两个区别：一、传统的梯度上升算法变量h和误差error都是向量，随机梯度上升算法则都是数值。二、随机梯度上升算法没有矩阵的转换过程，所有变量的数据类型都是NumPy数组。对于随机梯度上升算法，每次迭代只用一组数据，即可更新weights，故又称在线学习算法。随机梯度上升算法回归系数与迭代次数的关系图。可以看到数据逐渐趋于平衡，但是会出现周期性抖动，这也就是改进的随机梯度上升算法需要解决的地方。

(5)改进的随机梯度上升算法

def improRandGradAscent(dataSet, label, numIter=150):
    dataSet = np.array(dataSet)  # list转换为array
    label = np.array(label).T  # list转换为array
    m, n = dataSet.shape  # m参与训练数据集数，n表示每组的维度
    weights = np.ones(n)  # 初始权值都为1
    weights = np.array(weights)
    for j in range(numIter):
        dataIndex = [x for x in range(m)]  # 0-(numIter-1)
        for i in range(m):  # 迭代m次，所有数据参与迭代的次数
            alpha = 4 / (1.0 + i + j) + 0.01  # 学习速率，周期波动，总体收敛于0.01
            # 每次内循环迭代不规律，以免周期振荡
            randIndex = int(random.uniform(0, len(dataIndex)))
            h = sigmoid(sum(dataSet[randIndex] * weights))
            error = label[randIndex] - h  # 差
            weights = weights + alpha * error * dataSet[randIndex]  # 更新权值
            del (dataIndex[randIndex])  # 删除已被用数据集
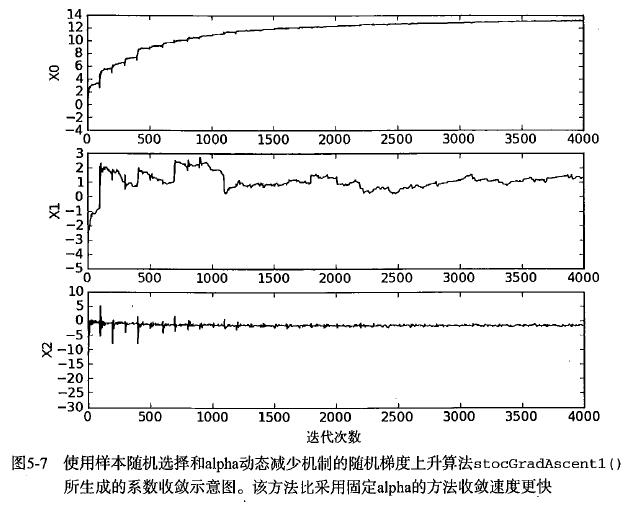
    return weights

　　改进的随机梯度上升算法相对于随机梯度上升算法，有两处得到了改进：一、alpha在每次迭代的时候都会有所改进，从公式来看体现在随着i与j的增大，alpha的值会有所变小，但是有0.01的系数相加，也不会导致数据集过多之后alpha的值过小，保证了在多次迭代之后新数据任然具有一定的影响。会让系统趋向于收敛。二、第二个改进的地方在于通过随机选取样本来更新回归系数，在代码中，也就是dataIndex = [x for x in range(m)]有所体现。这样可以减少周期性的波动，改进的随机梯度上升算法回归系数与迭代次数的关系图如下所示。此外，改进的算法还添加了一个迭代次数作为第三个参数，如果这个参数没有给定的话，算法将默认迭代150次。

(6)算法应用

　　下面提出这种算法的应用实例，输入一部分数据，也就是horseColicTraining.txt作为样本，经过随机梯度上升算法得出回归直线的方程，并应用该方程作为验证数据的方程。根据测试集horseColicTest.txt的输入带入到回归方程来验证其label与真实数据的之间的误差。值得记录的是，在项目中我的数据没有具体的label，仅有频率与幅度作为二维数据，并且通过此方法预测出来的回归方程为线性，带入到实际使用测试时，应该无法做出准确预测，只能观察其大致趋势。但是在实际数据中，数据往往不太可能是完全的线性，拟合的结果可能为折线、曲线等表现效果更好。因此，在测试数据的特征较少情况下，获得的效果可能并不理想。
　　下面的Demo使用了二十多个特征，来预测一个label，因此预测效果很好，错误率达到0%，因此在较多特征来表达一个结果的数据集中，该数据回归测试方式效果很好。

def classifyVector(xVec, weights):
    xVec = np.array(xVec)  # list转换为array
    weights = np.array(weights)  # list转换为array
    prob = sigmoid(sum(xVec * weights))
    if prob > 0.5:
        return 1.0
    else:
        return 0.0

def dieOfhorseTest():
    frTrain = open("horseColicTraining.txt")  # 训练数据
    frTest = open("horseColicTest.txt")  # 测试数据
    trainDataSet = []  # 存储训练数据
    trianLabels = []  # 存储对应的标签
    for line in frTrain.readlines():
        words = line.strip().split("\t")
        words = [float(word) for word in words]
        trainDataSet.append(words[0:-1])  # 前n-1个数据是一组数据
        trianLabels.append(words[-1])  # 第n个是标签
    # 训练求的权值
    weights = randGradAscent(trainDataSet, trianLabels)
    errorCount = 0.0  # 测试分类错误的个数
    testCount = 0.0  # 参与测试的总个数
    for line in frTest.readlines():
        testCount += 1  # 测试数加1
        words = line.strip().split("\t")
        words = [float(word) for word in words]
        # 分类不正确
        if classifyVector(words[0:-1], weights) != int(words[-1]):
            errorCount += 1  # 错误数加1
        errorRate = float(errorCount) / testCount  # 对应的错误率
        print("the error rate of this test is", errorRate)
        return errorRate

def multiTest():
    mulTests = 10  # 重复测试次数
    errorRate = 0.0
    for i in range(mulTests):
        errorRate += dieOfhorseTest()  # 总错误率
    # 输出总重复次数，平均错误率
    print("after %d interations , the average error rate is:%f\
    " % (mulTests, errorRate / mulTests))

def plotBestFit():
    import matplotlib.pyplot as plt
    dataSet, labels = loadDataset()  # 导入数据集
    weights = gradAscent(dataSet, labels)  # 训练数据
    weights = np.array(weights)
    label1X = []  # 存放A类数据的x坐标
    label1Y = []  # 存放A类数据的x坐标
    label2X = []  # 存放B类数据的x坐标
    label2Y = []  # 存放B类数据的x坐标
    for i in range(len(dataSet)):
        if int(labels[i]) == 1:  # 属于A类
            # dataSet[i],由x0,x1,x2组成
            label1X.append(dataSet[i][1])  # 存储x坐标
            label1Y.append(dataSet[i][2])  # 存储x坐标
        else:  # 属于A类
            label2X.append(dataSet[i][1])  # 存储x坐标
            label2Y.append(dataSet[i][2])  # 存储x坐标
    fig = plt.figure()
    ax = fig.add_subplot(111)
    # 在图上已不同的形式画出来
    ax.scatter(label1X, label1Y, s=30, c='red', marker='s')
    ax.scatter(label2X, label2Y, s=30, c='green')
    X = np.arange(-3.0, 3.0, 0.1)
    # x0*w0+x1*w1+x2*w2 = 0
    # x2=(-x0*w0-x1*w1)/w2
    # x2及是y
    Y = [(-weights[0] - weights[1] * x1) / weights[2] for x1 in X]
    ax.plot(X, Y)
    plt.xlabel('X1')  # 画出x轴标签
    plt.ylabel('X2')  # 画出y轴标签
    plt.show()  # 显示图

if __name__ == "__main__":
    plotBestFit()
    multiTest()

四、项目代码

　　整篇文章的代码以及数据集，我已经放到我的GitHub上，欢迎大家前往下载提出意见~（传送门）

Reference

　　本文的代码部分解释，参考这位老哥的博客。不得不吐槽一下这个编写博客的公式编辑功能，很难用，或者我还没仔细研究过。。就用Word编写贴上来了。毕竟是机器学习的第一篇文章，后面的学习要继续加油~