【机器学习】数据降维—线性判别分析(LDA)
本文代码推荐使用Jupyter notebook跑,这样得到的结果更为直观。
线性判别分析(Linear Discriminant Analysis,LDA)是一种可作为特征抽取的技术
LDA可以提高数据分析过程中的计算效率,对于未能正则化的模型,可以降低维度灾难带来的过拟合。
LDA与PCA相似:
PCA试图寻找到方差最大的正交的主成分分量轴,
LDA发现可以最优化分类的特征子空间
LDA和PCA都是可用于降低数据集维度的线性转换技巧。
PCA是无监督算法
LDA是监督算法
LDA是一种更优越的用于分类的特征提取技术
二分类中的LDA图:
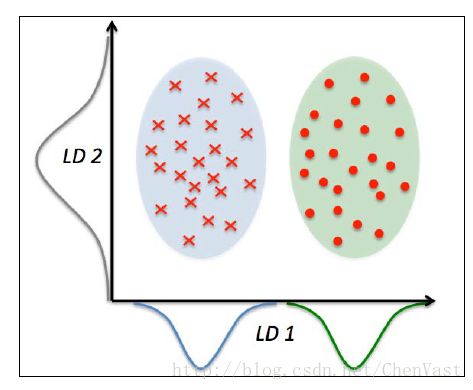
LD1通过线性判定,可以很好的将呈正态分布的两个类分开。
LD2的线性判定保持了数据集的较大方差,但LD2无法提供关于类别的信息,因此LD2不是一个好的线性判定。
LDA方法步骤:
1、 对d维数据集进行标准化处理(d为特征数量)
2、 对每一类别,计算d维的均值向量
3、 构造类间的散布矩阵以及类内的散布矩阵
4、 计算矩阵的特征值所对应的特征向量,
5、 选取前k个特征值对应的特征向量,构造一个d x k维的转换矩阵W,特征向量以列的形式排列
6、 使用转换矩阵W将样本映射到新的特征子空间上
计算散布矩阵:
均值向量m存储了类别i中样本的特征均值μm
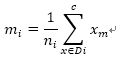
# 数据集的三个类别对应的均值向量
np.set_printoptions(precision=4)
mean_vecs = []
for label in range(1,4):
mean_vecs.append(np.mean(X_train_std[y_train==label], axis=0))
print('MV %s: %s\n' %(label, mean_vecs[label-1]))
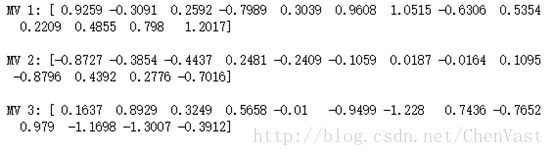
通过均值向量计算类内散布矩阵Sw:

通过累加各类别i的散布矩阵Si来计算:
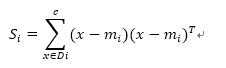
d = 13 # number of features
S_W = np.zeros((d, d))
for label,mv in zip(range(1, 4), mean_vecs):
class_scatter = np.zeros((d, d)) # scatter matrix for each class
for row in X[y == label]:
row, mv = row.reshape(d, 1), mv.reshape(d, 1) # make column vectors
class_scatter += (row-mv).dot((row-mv).T)
S_W += class_scatter # sum class scatter matrices
print('Within-class scatter matrix: %sx%s' % (S_W.shape[0], S_W.shape[1]))
print('Class label distribution: %s'
% np.bincount(y_train)[1:])
# 训练集的类标不均匀分布
因此计算散布矩阵前,对各类别的散布矩阵做缩放处理。
协方差矩阵可以看做归一化的散布矩阵

# 类内散布矩阵计算
d = 13 # number of features
S_W = np.zeros((d, d))
for label,mv in zip(range(1, 4), mean_vecs):
class_scatter = np.cov(X_train_std[y_train==label].T)
S_W += class_scatter
print('Scaled within-class scatter matrix: %sx%s' % (S_W.shape[0], S_W.shape[1]))
计算类间散布矩阵:
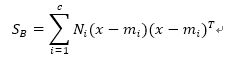
# 计算类间散射矩阵:
mean_overall = np.mean(X_train_std, axis=0)
d = 13 # number of features
S_B = np.zeros((d, d))
for i,mean_vec in enumerate(mean_vecs):
n = X[y==i+1, :].shape[0]
mean_vec = mean_vec.reshape(d, 1) # make column vector
mean_overall = mean_overall.reshape(d, 1) # make column vector
S_B += n * (mean_vec - mean_overall).dot((mean_vec - mean_overall).T)
print('Between-class scatter matrix: %sx%s' % (S_B.shape[0], S_B.shape[1]))
在新特征子空间上选取线性判别算法
eigen_vals, eigen_vecs = np.linalg.eig(np.linalg.inv(S_W).dot(S_B))# 特征值降序排序
#列出(特征值,特征向量)元组。
eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:,i]) for i in range(len(eigen_vals))]
# 从高到低排序(特征值,特征向量)元组。
eigen_pairs = sorted(eigen_pairs, key=lambda k: k[0], reverse=True)
# 通过减少特征值来直观地确定列表是否正确排序。
print('Eigenvalues in decreasing order:\n')
for eigen_val in eigen_pairs:
print(eigen_val[0])

d x d维协方差矩阵的秩最大为d-1,得到两个非0的特征值。
# 度量线性判别可以获得多少可区分类别信息
tot = sum(eigen_vals.real)
discr = [(i / tot) for i in sorted(eigen_vals.real, reverse=True)]
cum_discr = np.cumsum(discr)
plt.bar(range(1, 14), discr, alpha=0.5, align='center',
label='individual "discriminability"')
plt.step(range(1, 14), cum_discr, where='mid',
label='cumulative "discriminability"')
plt.ylabel('"discriminability" ratio')
plt.xlabel('Linear Discriminants')
plt.ylim([-0.1, 1.1])
plt.legend(loc='best')
plt.tight_layout()
# plt.savefig('./figures/lda1.png', dpi=300)
plt.show()
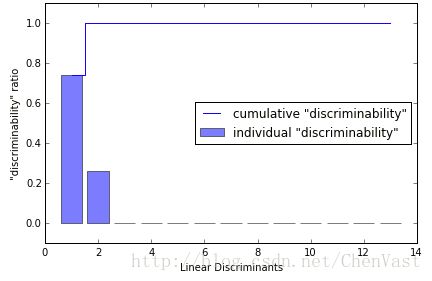
# 叠加两个判别能力最强的特征向量列来构建转换矩阵W
w = np.hstack((eigen_pairs[0][1][:, np.newaxis].real,
eigen_pairs[1][1][:, np.newaxis].real))
print('Matrix W:\n', w)

将样本映射到新的特征空间
# 对训练集进行转换X’=XW
X_train_lda = X_train_std.dot(w)
colors = ['r', 'b', 'g']
markers = ['s', 'x', 'o']
for l, c, m in zip(np.unique(y_train), colors, markers):
plt.scatter(X_train_lda[y_train==l, 0],
X_train_lda[y_train==l, 1],
c=c, label=l, marker=m)
plt.xlabel('LD 1')
plt.ylabel('LD 2')
plt.legend(loc='upper right')
plt.tight_layout()
# plt.savefig('./figures/lda2.png', dpi=300)
plt.show()

使用SKlearn进行LDA分析
from sklearn.lda import LDA
lda = LDA(n_components=2)
X_train_lda = lda.fit_transform(X_train_std, y_train)
# 逻辑回归在相对低维数据上的表现
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
lr = lr.fit(X_train_lda, y_train)
plot_decision_regions(X_train_lda, y_train, classifier=lr)
plt.xlabel('LD 1')
plt.ylabel('LD 2')
plt.legend(loc='lower left')
plt.tight_layout()
# plt.savefig('./figures/lda3.png', dpi=300)
plt.show()
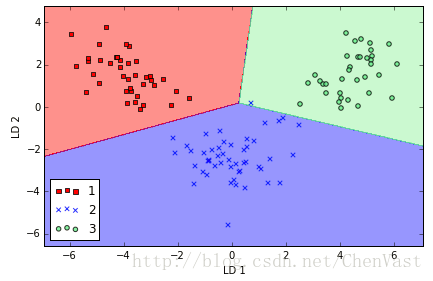
# 应用在测试集上的效果
X_test_lda = lda.transform(X_test_std)
plot_decision_regions(X_test_lda, y_test, classifier=lr)
plt.xlabel('LD 1')
plt.ylabel('LD 2')
plt.legend(loc='lower left')
plt.tight_layout()
# plt.savefig('./figures/lda4.png', dpi=300)
plt.show()
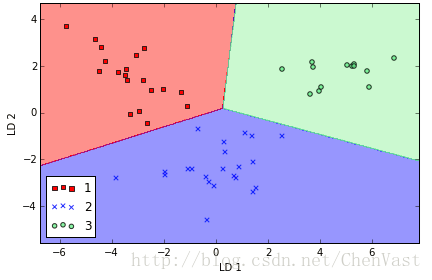
模型效果完美!