随机优化算法---爬山法VS模拟退火法

随机优化算法–爬山法VS模拟退火算法

随机优化算法，由于开始和过程都是随机的数值，所以每次产生的结果都不一样。但大致收敛方向是一致的。
爬山法是一种局部最优的算法（本质上属于贪心法），也属于启发式的方法，它一般只能得到局部最优解。采用启发式方法，是对深度优先搜索的一种改进，它利用反馈信息帮助生成解的决策。当优化的问题的局部最优解即为全局最优解时可以用此方法来求最优问题，否则可以考虑多次爬山法或者其他的方法如遗传算法和模拟退火法。

一、爬山算法

（1）爬山算法即是模拟爬山的过程，随机选择一个位置爬山，每次朝着更高的方向移动，直到到达山顶，即每次都在临近的空间中选择最优解作为 当前解，直到局部最优解。这样算法会陷入局部最优解，能否得到全局 最优解取决于初始点的位置。初始点若选择在全局最优解附近，则就可能得到全局最优解。

（2）爬山过程

function HILL-CLIMBING(problem) returns a state that is a local maximum
inputs: problem, a problem
local variables: current, a node
neighbor, a node
current <- MAKE-NODE(INITIAL-STATE[problem])
loop do
neighbor <- a highest-valued successor of current
if VALUE[neighbor]<= VALUE[current] then return STATE[current]
current <- neighbor

算法解释：
从当前的节点开始，和周围的邻居节点的值进行比较。 如果当前节点是最大的，那么返回当前节点，作为最大值(既山峰最高点)；反之就用最高的邻居节点来，替换当前节点，从而实现向山峰的高处攀爬的目的。如此循环直到达到最高点。

（3）存在的缺点
爬山法一般有下面3个问题：

（a）局部最大： 局部最大一般比状态空间中全局最大要小，一旦到达了局部最大，算法就会停止，即便该答案可能并不能让人满意。

（b）平顶（Plateau）：
平顶是状态空间中评估函数值基本不变的一个区域，在某一局部点周围f（x）为常量。一旦搜索到达了一个平顶，搜索就无法确定要搜索的最佳方向，会产生随机走动，这使得搜索效率降低。

（c）山脊（Ridge）：
山脊可能具有陡峭的斜面，所以搜索可以比较容易地到达山脊的顶部，但是山脊的顶部到山峰之间可能倾斜得很平缓，搜索的前进步伐会很小。

在每种情况中，算法都会到达一个点，使得算法无法继续前进。如果出现这种情况，可以从另外一个点重新启动该算法，这称为随机重启爬山法。爬山法是否成功和状态空间“表面”的形状有很大的关系：如果只有很少的局部最大，随机重启爬山法将会很快地找到一个比较好的解答。如果该问题是NP完全的，则该算法不可能好于指数时间，这是因为一定具有指数数量的局部最大值。然而，通常经过比较少的步骤，爬山法一般就可以得到比较合理的解答。

(4) 实验验证
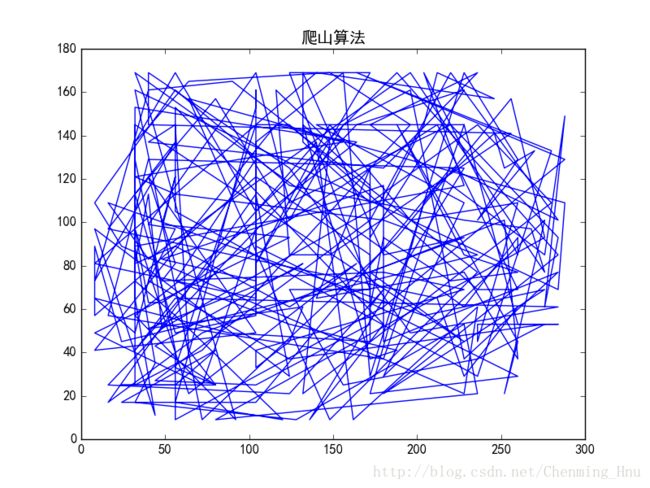
给定280个平面点（固定数据，方便与模拟退火法对比），运用爬山法进行找出“最优”路径：
爬山法算法求全局最短路径（数字代表第几个点）
最合适的路径为： [274, 226, 234, 213, 214, 247, 263, 19, 157, 23, 27, 146, 175, 192, 217, 233, 183, 86, 117, 62, 31, 152, 273, 239, 232, 0, 245, 16, 6, 269, 45, 39, 104, 170, 102, 124, 126, 209, 228, 272, 111, 87, 63, 168, 148, 180, 116, 84, 58, 108, 267, 271, 10, 5, 25, 71, 159, 156, 223, 193, 262, 261, 276, 277, 2, 255, 278, 7, 196, 24, 123, 174, 107, 57, 33, 155, 18, 14, 216, 237, 199, 268, 115, 158, 122, 113, 181, 201, 197, 127, 134, 144, 163, 91, 136, 9, 240, 260, 164, 96, 172, 101, 93, 171, 89, 177, 176, 88, 179, 182, 162, 161, 206, 140, 112, 114, 43, 160, 77, 125, 131, 56, 59, 266, 251, 78, 70, 74, 121, 138, 198, 173, 73, 80, 42, 61, 151, 76, 169, 118, 30, 29, 100, 187, 109, 83, 55, 103, 99, 142, 1, 22, 279, 218, 60, 41, 38, 143, 189, 259, 44, 75, 200, 274, 20, 257, 195, 243, 222, 225, 15, 252, 229, 205, 265, 145, 141, 186, 94, 17, 8, 137, 133, 178, 207, 224, 248, 147, 215, 53, 82, 98, 69, 184, 120, 95, 106, 253, 139, 26, 128, 135, 275, 242, 185, 130, 28, 150, 149, 3, 46, 49, 153, 202, 235, 110, 79, 129, 191, 210, 220, 65, 68, 37, 154, 256, 246, 230, 12, 85, 67, 203, 231, 194, 238, 13, 119, 36, 54, 35, 21, 270, 105, 92, 52, 132, 81, 165, 47, 50, 211, 249, 250, 11, 258, 64, 90, 97, 188, 212, 221, 166, 244, 4, 264, 167, 51, 236, 241, 34, 190, 208, 32, 48, 72, 40, 66, 204, 219, 227]
路径节点个数： 280
最小花费为： 23486.37
尝试次数: 280

二、模拟退火法

(1)简介： 模拟退火算法来源于固体退火原理，是一种基于概率的算法，将固体加温至充分高，再让其徐徐冷却，加温时，固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小。

(2)过程：
模拟退火算法的模型
1模拟退火算法可以分解为解空间、目标函数和初始解三部分。
2模拟退火的基本思想:

(1) 初始化：初始温度T(充分大)，初始解状态S(是算法迭代的起点)，每个T值的迭代次数L
(2) 对k=1, …, L做第(3)至第6步：
(3) 产生新解S′
(4) 计算增量ΔT=C(S′)-C(S)，其中C(S)为评价函数
(5) 若ΔT<0则接受S′作为新的当前解，否则以概率exp(-ΔT/T)接受S′作为新的当前解.
(6) 如果满足终止条件则输出当前解作为最优解，结束程序。
终止条件通常取为连续若干个新解都没有被接受时终止算法。
(7) T逐渐减少，且T->0，然后转第2步。

（3）优缺点：
优点是局部搜索能力强，运行时间较短；
缺点是全局搜索能力差，容易受参数的影响。

(4) 实验验证
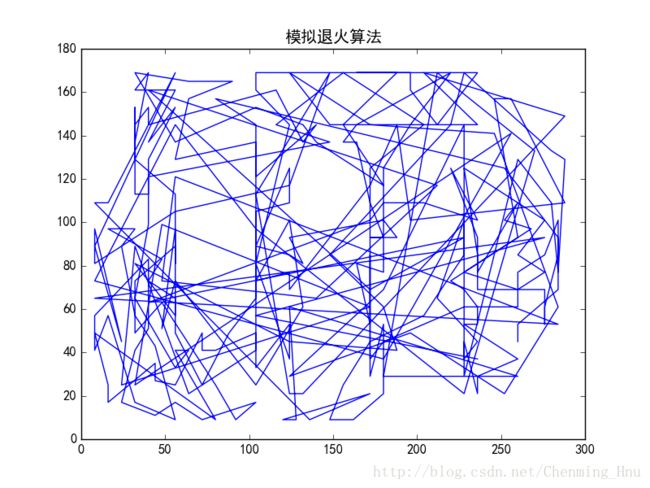
给定280个平面点（固定数据，方便与爬山法对比），运用爬山法进行找出“最优”路径：
模拟退火算法查找最优路径：
最合适的路径为： [217, 174, 244, 73, 234, 42, 112, 178, 261, 48, 146, 253, 87, 136, 267, 262, 255, 260, 257, 254, 208, 247, 248, 246, 205, 206, 210, 213, 212, 224, 218, 221, 215, 216, 214, 204, 256, 252, 203, 198, 192, 190, 191, 194, 143, 196, 138, 144, 148, 140, 139, 269, 270, 9, 17, 131, 132, 135, 265, 137, 264, 266, 151, 177, 150, 156, 153, 152, 119, 159, 173, 169, 107, 110, 86, 115, 66, 63, 65, 81, 89, 99, 97, 75, 77, 74, 85, 88, 79, 96, 98, 100, 167, 164, 165, 170, 171, 111, 80, 83, 116, 114, 59, 55, 52, 56, 57, 58, 44, 38, 45, 37, 51, 49, 54, 53, 47, 46, 28, 128, 20, 121, 122, 123, 41, 34, 32, 35, 50, 40, 29, 127, 129, 268, 18, 13, 22, 23, 12, 14, 272, 8, 6, 26, 25, 31, 30, 126, 157, 183, 181, 162, 160, 172, 105, 106, 101, 91, 90, 95, 94, 76, 166, 103, 104, 102, 82, 62, 43, 130, 125, 24, 271, 133, 147, 197, 199, 211, 227, 229, 245, 240, 238, 232, 233, 231, 209, 251, 259, 243, 250, 230, 228, 207, 249, 5, 4, 241, 263, 15, 134, 175, 176, 158, 155, 179, 163, 113, 108, 117, 109, 84, 182, 201, 142, 149, 273, 7, 279, 1, 237, 242, 278, 219, 258, 274, 141, 184, 202, 222, 235, 276, 16, 27, 19, 275, 11, 0, 185, 186, 120, 21, 154, 60, 71, 69, 78, 70, 36, 67, 68, 189, 193, 187, 188, 180, 223, 195, 10, 2, 220, 118, 39, 72, 200, 3, 92, 61, 145, 93, 64, 168, 161, 124, 33, 277, 239, 236, 226, 225]
路径节点个数： 280
最小花费为：
尝试次数: 280
可以发现，对于相同的数据，路径花费模拟退火（12589.76）明显比爬山法（23486.37）要小。

三、附件

https://pan.baidu.com/s/1eT5i0T0
包含上述280个点数据、爬山算法、模拟退火算法的实现。
本人 win10系统、内存8G、intel双核i5使用Pycharm IDE、Python 2.7.6版本。结果如上述，