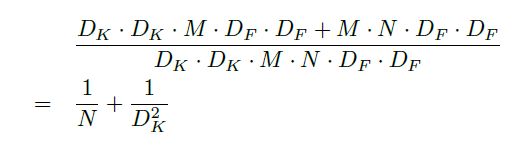mobileNet-一个典型的网络加速的例子

论文链接：https://arxiv.org/abs/1704.04861

MXNet框架代码：https://github.com/miraclewkf/mobilenet-MXNet

moblileNet,顾名思义，可以在移动端使用的网络，那必然要求网络的计算量要小一些，不然移动端可扛不住啊，那MobileNet如何做到这个的呢？？总结来看，其主要创新点就在于论文中反复强调的depth-wise separable convolutions，作者将其操作分成两步，一部分是depthwise convolution,另一部分是pointwise convolution，通过这种方法，将网络的复杂度降下来，使得可以在移动端、嵌入式平台中使用。

那么MobileNet是怎么做的呢？

首先介绍一下论文的核心：Depthwise Separable Convolution

Depthwise Separable Convoltion类似于一种因式分解，比如你求面积，可以使用长乘以宽一样，moblieNet就是将一个完整的卷积分为两部分：depthwise convolution以及1*1的pointwise convolution, depthwise对特征图的每个channel进行卷积，pointwise convolution将depthwise的结果进行合并。如下图所示，图（a）为一个标准的卷积计算，标准的卷积需要将filter与各个channel相乘，然后求和得到一个卷积结果。图（b）代表着depthwise convolution,其将每个filter与每个channel单独相乘，并不求和，得到与原来channel相同的特征图，然后利用图（c）代表pointwise convolution，将各个特征图求和。

下面详细说明一下：

在标准的卷积中假设输入为$D_F\ast D_F\ast M$的特征图F,其中M为通道数（channel），输出为$D_G\ast D_G\ast N$的特征图G,利用卷积核大小为$M\ast D_K\ast D_K\ast N$,标准的卷积计算的计算量为：$D_K\ast D_K\ast M\ast N\ast D_F\ast D_F$这里当然是估算，stride=1时，大概是这个数，至于moblileNet呢？首先使用M个$D_K\ast D_K$的卷积核，如图（b）所示，对每个channel进行处理(这里其实就是一个group 卷积处理，group数量等于channel数量，就实现了每个卷积核对每个channel处理)，这里的计算量是$D_K\ast D_K\ast M\ast D_F\ast D_F$，但是这并没有将channel信息进行融合，所以作者接着使用N个1*1的卷积进行channel的合并，这里的计算量是$M\ast N\ast D_F\ast D_F$,所以总的计算量是原来的（这里直接上图，打公式有点费劲）：

这里作者介绍到，如果使用3*3的depthwise separable convolutions可以减少8-9倍的计算量，后面的表格也证明了这一点

网络block的实现如下所示，不管你用不用MXNET，代码应该可以看懂

def Conv(data, num_filter=1, kernel=(1, 1), stride=(1, 1), pad=(0, 0), num_group=1, name='', suffix=''):
    conv = mx.sym.Convolution(data=data, num_filter=num_filter, kernel=kernel, num_group=num_group, stride=stride, pad=pad, no_bias=True, name='%s%s_conv2d' % (name, suffix))
    bn = mx.sym.BatchNorm(data=conv, name='%s%s_batchnorm' % (name, suffix), fix_gamma=True)
    act = mx.sym.Activation(data=bn, act_type='relu', name='%s%s_relu' % (name, suffix))
    return act


def Conv_DPW(data, depth=1, stride=(1, 1), name='', idx=0, suffix=''):
    conv_dw = Conv(data, num_group=depth, num_filter=depth, kernel=(3, 3), pad=(1, 1), stride=stride, name="conv_%d_dw" % (idx), suffix=suffix)
    conv = Conv(conv_dw, num_filter=depth * stride[0], kernel=(1, 1), pad=(0, 0), stride=(1, 1), name="conv_%d" % (idx), suffix=suffix)
    return conv

Network Structure

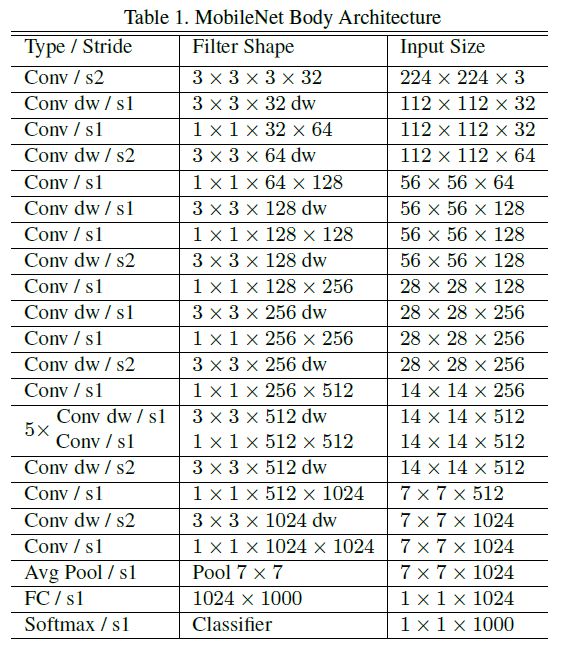
MobileNet的结构如下图（共28层）：

MobileNet中的所有层都接了BN层以及ReLU层，下采样层，采用depthwise convolution中的stride进行，最后接了全局平均池化层

作者还提到了一点是：非结构化的稀疏矩阵，并不一定比密集矩阵快，除非是高程度的稀疏

下图中介绍了采用这个方法各个层的参数占比：

进一步减少参数的手段(一)：Width Multiplier: Thinner Models

虽然到这里，参数已经降低很多了，但是作者并不满足，而是想办法继续降低参数量，怎么做的呢？作者引入了一个参数$\alpha$,被称作宽度乘子，作用呢就是降低网络的宽度，同时将网络每层的输入与输出降低到原来的$\alpha$倍，$\alpha$一般被设置为1，0.75，0.5，0.25

$D_K\ast D_K\ast \alpha M\ast D_F\ast D_F+\alpha M\ast N\ast D_F\ast D_F$

进一步减少参数的手段(二)：Resolution Multiplier: Reduced Representation

该方法通过按照比例降低输入图像以及每层的特征图大小来减少参数量，同样比较直观，公式如下：

$D_K\ast D_K\ast \alpha M\ast \rho D_F\ast \rho D_F+\alpha M\ast N\ast \rho D_F\ast \rho D_F$

论文主打就是降低网络的计算量，那么该方法究竟可以降低多少计算量呢？看下面一张表格，这是一个layer的例子，只是用depthwise separable conv降低了约9倍的计算量，如果再加上上面的那两个手段，降低了30来倍呀

做了这么多，参数降低了这么多，那么网络的精度会怎么样呢？这里是作者的实验结果：

首先在imagenet上面的实验，上面是全卷积网络，下面是mobileNet网络，可见，参数量降低了大约9倍，但是精度只是减少了约1%。：

接下来就是作者的一顿穷举，各个参数，各个数据集，对比网络的参数量以及精度，这里就不详细介绍了，想了解的读者可以查看论文。

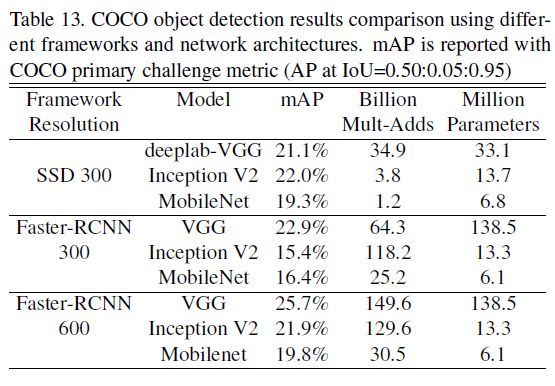
这里介绍一个在COCO数据集上进行检测的实验结果：

------很久之后再看的反思（学而时习之，真的很重要）-----
其实这篇论文，核心思想就是要减少计算量，那么怎么减少呢？

• 通过分组卷积来减少计算量（并增加了point-wise来进行channel之间的交互）
• 通过分组卷积（depth-wise）,可以将计算量减少8-9倍，这时候1x1的卷积计算量就凸显出来了。
• 从channel的角度继续减少计算量：引入了一个参数$\alpha$，控制channel的数量，进一步减少计算量。
• 从特征图大小的角度减少计算量：引入一个参数$\beta$，对特征图比例进行缩放控制。

下面从计算量公式上进行理解，如下：

原本计算量：$D_K\ast D_K\ast M\ast N\ast D_F\ast D_F$
分组卷积后：$D_K\ast D_K\ast M\ast D_F\ast D_F+M\ast N\ast D_F\ast D_F$
上面公式中$D_K$已经是3x3的了不能动了，N是输入channel不能动了，那想继续降低参数只能在M和$D_F$上下功夫了，所以：
在M上下功夫，减少channel：$D_K\ast D_K\ast \alpha M\ast D_F\ast D_F+\alpha M\ast N\ast D_F\ast D_F$
进一步在$D_F$上下功夫：$D_K\ast D_K\ast \alpha M\ast \rho D_F\ast \rho D_F+\alpha M\ast N\ast \rho D_F\ast \rho D_F$

仅此而已