线性筛/欧拉筛（知识整理+板子总结）

欧拉筛就是一类强行把筛降到线性O(n)的筛，

是线性筛的一种叭……

我对定义这种东西不大了解……

以下整理几种欧拉筛

筛素数prime、欧拉函数phi(n)、莫比乌斯函数μ(n)

并给出一定的证明过程

 

①素数筛

typedef long long ll;
bool ok[maxn];
int prime[maxn],cnt;
void sieve()
{
	for(ll i=2;i=maxn)break;
			ok[i*prime[j]]=1;
			if(i%prime[j]==0)break; 
		}
	}
}

每次用已筛出来的质数去筛更大的数，

每个合数只被它最小的质因子筛掉，

试想，如果2*6筛了12之后还没break，

而是用3*6筛掉18，那么18还会被2*9筛一次，就重复了

而根本原因就是6有2这个因子，

而3*6筛掉的数一定也有2这个因子，

3*6这个数应该被2这个因子筛掉，而不是3

②欧拉函数筛（）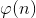

typedef long long ll;
bool ok[maxn];
int prime[maxn],phi[maxn],cnt;
void sieve()
{ 
        phi[1]=1;
	for(ll i=2;i=maxn)break;
			ok[i*prime[j]]=1;
			if(i%prime[j]==0)
			{
				phi[i*prime[j]]=phi[i]*prime[j];//prime[j]是i的因子 prime[j]的素因子项包含在i的素因子项里
				break; 
			}
			else phi[i*prime[j]]=phi[i]*(prime[j]-1);//prime[j]与i互质 phi[i*prime[j]=phi[i]*phi[prime[j]]
		}
	}
}

思路来源

https://blog.csdn.net/bojack_/article/details/78313778

解释

其实就是看prime[j]是否已经在i中出现过了，第一次出现要减1，后面的不减

特判n==1，phi[1]=1

如果，pi为素因子，

那

对于i*prime[j]，

①i%prime[j]==0，prime[j]是素数，所以i包含prime[j]这个素因子，i是prime[j]的倍数

故

由于i里面有等素因子，故

所以

②i%prime[j]!=0，又prime[j]是素数，所以i里面没有prime[j]这个素因子，所以i和prime[j]互素

由欧拉函数的积性可知，

而

故

③莫比乌斯函数筛（）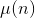

typedef long long ll;
bool ok[maxn];
int prime[maxn],mu[maxn],cnt;
void sieve()
{
	mu[1]=1;
	for(ll i=2;i=maxn)break;
			ok[i*prime[j]]=1;
			if(i%prime[j]==0)
			{
				mu[i*prime[j]]=0;//如果开的是全局,就不用管 
				break; 
			}
			else mu[i*prime[j]]=-mu[i];
		}
	}
}

图片来自百度百科：莫比乌斯函数

特判n==1，mu[1]=1

对于一个素数p，μ(p)=-1

而一个数i*prime[j]被最小素因子prime[j]筛到的时候，

①i%prime[j]!=0,i里没有prime[j]这个素因子

i*prime[j]是比i多一个素因子prime[j]的，

所以μ(i*prime[j])=-μ(i)即可

②i%prime[j]==0，i里有prime[j]这个素因子

说明i*prime[j]里至少有两个prime[j]这个素因子，

根据莫比乌斯函数定义，μ(i*prime[j])=0，

开全局变量的话就不用管

 

搞个三合一板好了，以后直接粘着用……

#include
#include
#include
using namespace std;
typedef long long ll;
const int maxn=1e6+10;
bool ok[maxn];
int prime[maxn],phi[maxn],mu[maxn],cnt;
void sieve()
{
	phi[1]=mu[1]=1;
	for(ll i=2;i=maxn)break;
			ok[k]=1;
			if(i%prime[j]==0)
			{
				phi[k]=phi[i]*prime[j];
				mu[k]=0;
				break; 
			}
			else
			{
			 phi[k]=phi[i]*(prime[j]-1);
			 mu[k]=-mu[i];
		    }
		}
	}
}
int main()
{
	sieve();
    return 0;
}

④积性函数线性筛

思路来源：https://www.cnblogs.com/zwfymqz/p/9337898.html

 

线性筛中，k只会被最小素因子prime[j]筛到，

所以，分i是否有prime[j]这个素因子，是否全为prime[j]这个素因子来讨论

 

以2019南京网络赛 E.K Sum为例，这里，sieve中的f[]是一个积性函数

#include
#include
#include
#include